Complete Solutions to EXERCISE of chapter LINEAR PROGRAMMING of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | LINEAR PROGRAMMING |
| MODERN PUBLICATION | EXERCISE |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
Define objective function.
View SolutionState the feasible solution.
View SolutionState the extreme point theorem.
View SolutionTo which coordinate axis the line `x = 1` and `y = 2` is parallel.
View SolutionAn animal feed company must produce 200`kg` of a mixture consisting of ingredients A and B. The-ingredient A costs Rs.3 per `kg` and B costs 5 per `kg`. No more than 80 `kg` of A can be uséd and at least 60 `kg` of B must be used. Formulate the problem to minimise thé cost of mixture.
View SolutionA merchant sells two models X and Y of TV with cost price ₹ 25000 and ₹ 50000 Per set respectively. He gets a profit of ₹ 1500 on model X and ₹ 2000 on model Y . The sales connot exceed 20 sets in a month. If he cannot invest more than 6 lakh rupees, formulate the problem of determining the number of sets of each type he must keep in stock for maximum profit.
View SolutionA factory uses three different respurce for the manufacture of two different products, 20 units of the resource A, 12 units of B and 16 unit of C being available. One unit of the first product requires 2,2 and 4 units of the resources and one unit of the second product requires 4,2 and 0 units of the resources taken in order. It is known that the first product gives a profit of ₹20 per unit and the second ₹ 30 prt uniy. Formulate the LPP so as to earn maximum profit.
View SolutionAn agro-based company produces tomato souce and tomato jelly. The quantity of material, machine hour, labour (man hour) required to to produce one unit of each product and the avilability of raw material one given is the following table.
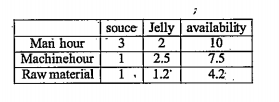 Assume that one unit of source and of unit of Jelly, yield a profit of Rs 2 and Rs 4 respectively. Formulate the L.P.P so as to yield maximum profit.
Assume that one unit of source and of unit of Jelly, yield a profit of Rs 2 and Rs 4 respectively. Formulate the L.P.P so as to yield maximum profit.
View Solution(Allocation Problem.)A farmer has 5 acres of land on which he wishes to grow two crops X and Y. He has to use 4 cart loads and 2cart loads of manure per acre for crops X and Y respectively. But not more than 18 cart loads of manure is available. Other expenses are ₹200 and ₹500 per acre for the crops X and Y respectively . He estimates profit from crops X and Y at the rates ₹1000 and ₹800 per acre respectively. Formulate the LPP as to how much land he should allocate to each crop for maximum profit.
View SolutionMaximise `Z=5x_(1)+7x_(2)`
Subject to `x_(1)+x_(2)le4`,
`5x_(1)+8x_(2)le24`
and `10x_(1)+7x_(2)le35,x_(1),x_(2)ge0`.
View SolutionSolve the following LPP
Minimise `Z=20x_(1)+10x_(2)`
Subject to `x_(1)+2x_(2)le40`
`3x_(1)+x_(2)ge30`
`x_(1),x_(2)ge0`.
View SolutionSolve the following LPP graphically Optimize `Z=5x_1+25x_2` subject to `-0.5x_1+x_2 le 2, x_1+x_2 ge 2, -x_1+5x_2 ge 5, x_1, x_2 ge 0`
View Solution
EXERCISE questions and complete solutions for chapter LINEAR PROGRAMMING of MODERN PUBLICATION of Class 12