Complete Solutions to ILLUSTRATIVE EXAMPLES of chapter VECTOR ALGEBRA of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | VECTOR ALGEBRA |
| MODERN PUBLICATION | ILLUSTRATIVE EXAMPLES |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
Classify the following measures as scalar and vector quantities :
(i) `40^(@)`
(ii) 50 watt
(iii) `10 gm//cm^(3)`
(iv) 20 m/sec towards north
(v) 5 seconds.
View SolutionIn the figure, which of the vectors are :
(i) Collinear
(ii) Equal
(iii) Co - initial.
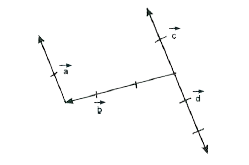
View SolutionProve that the resultant of the vectors represented by the sides `vec(AB)` and `vec(AC)` of a triangle ABC is `2 vec(AD)`, where D is the mid - point of [BC].
View SolutionShow that the sum of three vectors determined by the medians of a triangle directed from the vertices is zero.
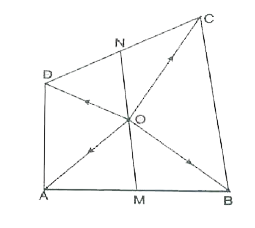
View SolutionIn the figure, M is the mid - point of [AB] and N is the mid - point of [CD] and O is the mid - point of [MN]. Prove that :
(i) `vec(OA)+vec(OB)+vec(OC)+vec(OD)=vec(0)`
(ii) `vec(BC)+vec(AD)=2vec(MN)`.
View Solution`A B C D` is parallelogram and `P` is the point of intersection of its diagonals. If `O` is the origin of reference, show that ` vec O A+ vec O B+ vec O C+ vec O D=4 vec O Pdot`
View Solution(a) What is the geometric significance of the relation `|vec(a)+vec(b)|=|vec(a)-vec(b)|` ?
(b) Prove geometrically that `|vec(a)+vec(b)|le |vec(a)|+|vec(b)|`.
View SolutionIf the sum of two unit vectors is a unit vector, prove that the magnitude of their difference is `sqrt(3.)`
View SolutionIf `D ,\ E ,\ F` are the mid points of the side `B C ,\ C A` and `A B` respectively of a triangle ABC, write the value of ` vec A D+ vec B E+ vec C Fdot`
View SolutionShow, by vector methods, that the angularbisectors of a triangle are concurrent and find an expression for the position vector of the point of concurrency in terms of the position vectors of the vertices.
View SolutionProve, by vector method, that the diagonals of a parallelogram bisect each other , conversely, if the diagonals of a quadrilateral bisect each other, it is a parallelogram.
View SolutionProve using vectors: The diagonals of a quadrilateral bisect each other iff it is a parallelogram.
View SolutionProve that the segment joining the middle points of two non-parallel sides of a trapezium is parallel to the parallel sides and half of their sum.
View Solution(Pythagorass Theorem) Prove by vector method that in a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
View SolutionProve using vectors: The median to the base of an isosceles triangle is perpendicular to the base.
View SolutionProve that the perpendicular let fall from the vertices of a triangle to the opposite sides are concurrent.
View SolutionProve that in any triangle ABC(i) `c^2 = a^2 + b^2-2ab cos C` (ii) `c=bcosA+acosB`
View SolutionShow that the diagonals of a rhombus are perpendicular to each other
View SolutionIn a tetrahedraon, if two pairs of opposite edges are perpendicular to each other, prove that the third pair is also perpendicular and that the sum of the squares on the two opposite edges is same for each pair.
View SolutionFor any `A, B` in `R`, prove that `cos (A-B) = cos A cos B + sin A sin B `
View SolutionFind the moment (torque) about the point `hat(i)+2hat(j)+3hat(k)` of a force represented by `hat(i)+hat(j)+hat(k)` acting through the point `-2hat(i)+3hat(j)+hat(k)`.
View SolutionTwo unlike forces of equal magnitudes `3hat(i)+hat(k)` and `-3hat(i)-hat(k)` acting at the points `hat(i)+2hat(j)-hat(k)` and `2hat(i)-hat(j)+3hat(k)` respectively. Find the moment of the coupie formed by the forces.
View SolutionWhat is the magnitude of the moment of the couple consisting of the force `vec(F)=3 hat(i)+2hat(j)-hat(k)` acting through the point `hat(i)-hat(j)+hat(k) and -vec(F)` acting through the point `2hat(i)-3hat(j)-hat(k)`?
View SolutionFind the moment about a line through (0, 0, 0) having the direction `2hat(i)-2hat(j)+hat(k)` due to a 20 kg force acting at `(-4, 2,5)` in the direction of `12 hat(i)-4hat(j)-3hat(k)`.
View Solution
ILLUSTRATIVE EXAMPLES questions and complete solutions for chapter VECTOR ALGEBRA of ARIHANT MATHS (HINGLISH) of Class 12
All Exercises from MODERN PUBLICATION Class 12 MATHS VECTOR ALGEBRA
- CHAPTER TEST 10
- COMPETITION FILE
- Exercise
- EXERCISE 10 (a) Short Answer Type Questions
- EXERCISE 10 (b) Short Answer Type Questions
- EXERCISE 10 (c ) Long Answer Type Questions (I)
- EXERCISE 10 (c ) Long Answer Type Questions (II)
- EXERCISE 10 (c ) Short Answer Type Questions
- EXERCISE 10 (d) Long Answer Type Questions (I)
- EXERCISE 10 (d) Long Answer Type Questions (II)
- EXERCISE 10 (e ) Long Answer Type Questions (I)
- EXERCISE 10 (e ) Long Answer Type Questions (II)
- EXERCISE 10 (e ) Short Answer Type Questions
- EXERCISE 10 (f) Short Answer Type Questions
- EXERCISE 10 (i) Long Answer Type Questions (I)
- EXERCISE 10 (i) Short Answer Type Questions
- EXERCISE 10 (j) Long Answer Type Questions (I)
- EXERCISE 10 (j) Long Answer Type Questions (II)
- EXERCISE 10 (j) Short Answer Type Questions
- Frequently Asked Questions (Example)
- ILLUSTRATIVE EXAMPLES
- Miscellaneous Exercise on Chapter 10
- Ncert File Question from Ncert Book (Exercise 10.1)
- Ncert File Question from Ncert Book (Exercise 10.2)
- Ncert File Question from Ncert Book (Exercise 10.3)
- Ncert File Question from Ncert Book (Exercise 10.4)
- Ncert File Question from Ncert Book (Exercise 10.5)
- Objective Type Questions (A. Multiple Choice Questions)
- Objective Type Questions (B. Fill in the Blanks)
- Objective Type Questions (C. True/False Questions)
- Objective Type Questions (D. Very Short Answers Type Questions)
- Questions From NCERT Exemplar (Example)
- Revision Exercise