Complete Solutions to Solved Examples of chapter ATOMS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ATOMS |
| MODERN PUBLICATION | Solved Examples |
| Number Of Questions | 33 |
| Academic Year | 2023-24 |
Calculate the distance of closest approach when a proton of energy 3 MeV approaches a gold nucleus (Z=79).
View SolutionCalculate the energy of an `alpha`-particle whose distance of closest approach with the gold nucleus is 29.5 fermi.
View SolutionAn `alpha`-particle of velocity `2.3xx10^7` m/s exhibits back scattering by a gold foil (Z=79).Predict the maximum possible radius of the gold nucleus approximately Charge of mass ratio for `alpha`-particle is `4.8xx10^7` C/kg.
View SolutionAn `alpha`-particle is accelerated through a potential of 1MV and falls on a silver foil (Z=47).
Calculate : (i)Kinetic energy of the `alpha`-particle when it falls on the foil .
(ii)Kinetic energy of the `alpha`-particle when it is `6.9xx10^(-14)` m distant from the nucleus .
(iii)Distance of closest approach to the nucleus .
View SolutionIn an `alpha`-particle scattering experiment , 100 particles are scattered per minute at an angle of `60^@` . Calculate the number of particles per minute scattered at an angle of `30^@`
View SolutionWhat is the impact parameter of an `alpha`-particle of initial energy 5 MeV scattered by `60^@` for Z=79 ?
View SolutionCalculate the angular momentum of an electron in the second orbit of an atom ?
View SolutionCalculate the radius of smallest orbit of a hydrogen atom.
View SolutionWhat is the velocity of electron in Bohr's third orbit of hydrogen atom ? Also calculate the number of revolutions the electron makes in Bohr's third orbit in one second.
View SolutionCalculate the speed of the electron in n=2 orbit of `Li^(+ +)`ion.
View SolutionThe energy of an electron in the nth orbit is given by `E_(n)=-13.6//n^(2) eV`. Calculate the energy required to excite an electron from ground state to the second excited state.
View SolutionCalculate the energy required to separate a hydrogen atom into a proton and an electron if the orbital radius is `5.3xx10^(-11)` m. Also calculate the velocity of the electron in a hydrogen atom.
View SolutionA `10kg` satellite circles earth once every `2hr` in an orbit having a radius of `8000km`. Assuming that Bohr's angular momentum postulate applies to satellites just as it does to an electron in the hydrogen atom, find the quantum number of the orbit of the satellite.
View SolutionIn the ground state of hydrogen atom, its Bohr radius is `5.3xx10^(-11)m`. The atom is excited such that the radius becomes `21.2xx10^(-11)m`. Find the value of principal quantum number and total energy of the atom in excited state.
View SolutionThe ground state energy of the hydrogen atom is 13.6 eV. Calculate
(i)the kinetic energy of the electron in the `1^(st)` excited state.
(ii)the potential energy of the electron in the `3^(rd)` excited state.
(iii)frequency of the photon emitted if the electron jumps from the `3^(rd)` excited state of `1^(st)` excited state.
View SolutionElectron in a hydrogen atom makes a transition from higher energy states to n=2. Calculate the maximum possible wavelengths in this transition.
View SolutionIn a hydrogen atom , an electron makes a transition from energy level of -1.51 eV to ground level . Calculate the wavelength of the spectral line emitted and identify the series of hydrogen spectrum to which this wavelength belongs.
View SolutionThe energy level diagram of an element is given below. Identify , by doing necessary calculation , which transition corresponds to the emission of a spectral line of wavelength 102.7 nm
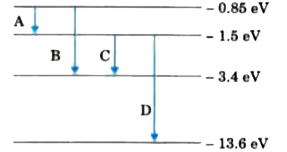
View SolutionEnergy level diagram of a hydrogen atom is shown below :
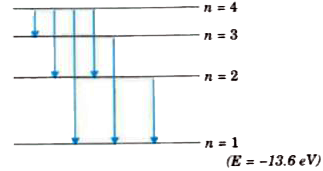
(i)If a transition takes place from n=3 to n=2 orbit, calculate the wavelength of the radiation emitted. Identify the spectral series to which it belongs.
(ii)Which transition results in emission of radiation of maximum wavelength ?
View SolutionIf the wavelength of the first member of Balmer series in hydrogen spectrum is 6563 Å, calculate the wavelength of the first member of Lymen series in the same spectrum.
View SolutionWhich is the shortest wavelength in the Balmer series of hydrogen atoms ?
View SolutionCalculate the longest wavelengths belonging to Lyman and Balmer series. Which of these wavelengths will lie in the visible region ?
View SolutionThe wavelength of `H_alpha` line in the Balmer series is 6563 Å . Compute the value of Rydberg constant and hence obtain the wavelength of `H_beta` line of Balmer series.
View SolutionA `12.9 eV` beam of electrons is used to bombard gaseous hydrogen atom at room temperature. Up to which energy level the hydrogen atoms would be excited?
Calculate the wavelength of the first member of Paschen series and first member of Balmer series.
View SolutionA proton traps a free electron to form the hydrogen atom of lowest energy level. If photon is emitted in this process then what will be its wavelength. Assume initial kinetic energy of the electron to be zero.
View SolutionWhich state of triply ionised Beryllium `(Be^(+++))` the same orbital radius as that of the ground state hydrogen ?
View SolutionFind the wavelengths in a spectrum of hydrogen atom between 600 nm to 700 nm
View SolutionCalculate the minimum wavelength emitted by an X-ray tube which is operated at a potential difference of 20 kV.
View SolutionA potential difference of 40,000 V is applied between the filament and the target metal inside X-ray tube. It is found that a current of 1 mA flows in the tube.
(i)How many electrons are hitting the target metal per second ?
(ii)Calculate the amount of energy falling on target metal per second in the form of kinetic energy of the electron .
(iii)What will be the cutoff wavelength of X-rays produced from this tube ?
View SolutionA potential difference of 40 kV is applied between the target metal and the filament of an X-ray tube . One electron gets accelerated through this potential difference and loses 10% of its kinetic energy in first collision. What will be the frequency of emitted photon ?
View SolutionThere is one isolated atom of iron which emits `K_alpha` X-rays of energy 6.4 keV . With what kinetic energy, the iron atom will recoil If mass of iron atom is `9.3xx10^(-26)` kg.
View SolutionHeat is produced at a rate of 250 J per second in an X-ray tube when potential difference of 20 kV is applied between filament and target metal. How much current flows through the tube ? Assume only a small fraction of kinetic energy of electrons is converted into X-rays.
View SolutionElectrons in a television are accelerated through a potential difference of 30 kV before they strike the screen. Calculate the wavelength of the most energetic X-ray photon emitted from it.
View Solution
Solved Examples questions and complete solutions for chapter ATOMS of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 12
All Exercises from MODERN PUBLICATION Class 12 PHYSICS ATOMS
- Chapter Practice Test
- COMPETITION FILE ( Matching )
- COMPETITION FILE ( Objective B (MCQs))
- COMPETITION FILE (Assertion & Reason )
- COMPETITION FILE (Integers )
- COMPETITION FILE (Matrix match )
- COMPETITION FILE (Ncert Exemplar Problems )
- COMPETITION FILE (Objective A(MCQs) )
- COMPETITION FILE (Objective BB (MCQs))
- COMPETITION FILE (Objective C (MCQs))
- COMPETITION FILE (Objective D (MCQs))
- Conceptual Questions
- Hots
- Ncert File
- Practice Problems
- Revision Exercise (Fill in the blanks )
- Revision Exercise (Long Answer )
- Revision Exercise (Numerical Problems )
- Revision Exercise (Short Answer )
- Revision Exercise (Very Short )
- Solved Examples
- Tough & Tricky Problems
- very short