Complete Solutions to Solved Example Type of chapter LINEAR PROGRAMMING of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | LINEAR PROGRAMMING |
| NAGEEN PRAKASHAN | Solved Example Type |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
Solve the Following Linear Programming Problem graphically : Maximise `Z = 3x + 4y` subject to the constraints : `x+ylt=4,xgeq0,ygeq0`.
View SolutionSolve the following linear programming problem graphically:
Minimize : `z=100x+50y`
Subject to constraints `: x+2yge10`
`3x+4yge24`
`xge0`
`yge0`
View SolutionSolve the following linear programming problem graphically.
Minimize `:z=2x+3y-1`
Subject to:
`x-yge0`
`-x+2yge2`
`xge3`
`yle4`
`yge0`
View SolutionSolve the following linear programming problem graphically:
Minimize: `z=x+3y`
Subject to:
`x+yle8`
`3x+5yge15`
`xge0`
`yge0`
View SolutionSolve the following linear programming problem graphically:
Maximize : `z=5x+3y`
Subject to:
`x+3yle5`
`x+yle3`
`xge0`
`yge0`
View SolutionA man wishes to mix two types of food `X` and `Y` in such a way that the vitamins contents of the mixture contain at least B units of vitamin A and 11 units of vitamin B. Food `X` costs Rs. 50 per kg and food `Y` costs Rs. 60 per kg. Fod `X`contains 2 units per kg of vitamin A and 5 kg per unit of vitamin B while food `Y` contains 5 units per kg of vitamin A and 2 units per kg of vitamin B. Determine the minimum cost of the mixture.
View Solution(Allocation problem) A cooperative society of farmers has 50 hectare of land to grow two crops X and Y. The profit from crops X and Y per hectare are estimated as Rs 10,500 and Rs 9,000 respectively. To control weeds, a liquid herbicide has to be
View SolutionA factory makes tennis rackets and cricket bats. A tennis racket takes `1. 5` hours of machine time and 3 hours of craftmans time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftmans time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsmans time. If the profit on a racket and on a bat is Rs. 20 and Rs. 10 respectively, find the number of tennis rackets and crickets bats that the factory must manufacture to earn the maximum profit. Make it as an L.P.P. and solve graphically.
View SolutionA manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs.17.50 per package on nuts and Rs.7 per package of bolts. How many packages of each should be produced each day so as to maximize his profits if he operates his machines for at the most 12 hours a day? Form the linear programming problem and solve it graphically.
View SolutionThere are factories located one at place `P` and other at place `Q` from which a certin commodity is to be delivered to each of three depot situated at A,B and C. The weekly requirement of the depots are respectively 5,5 and 4 units of the commodity while the production capacity of the factories `P` and `Q` are respectively 8 and 6 units. The cost of transportation per unit is given below.
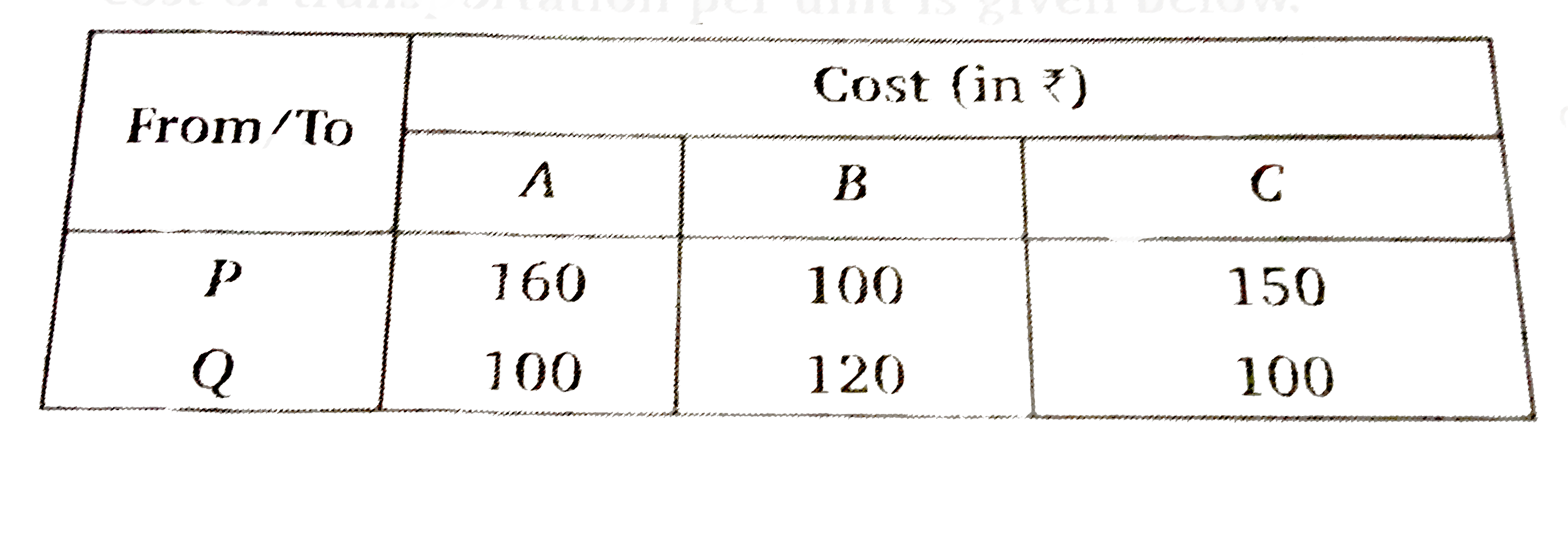
How many units should be transported from each factory to each depot in order that the transportation cost is minimum. Also find the minimum transportation cost.
View Solution
Solved Example Type questions and complete solutions for chapter LINEAR PROGRAMMING of NAGEEN MATHS (HINGLISH) of Class 12