Complete Solutions to COMREHENSION of chapter NUCLEAR CHEMISTRY of Class 12 book with complete answers and questions
| Class 12 | CHEMISTRY |
| Chapter | NUCLEAR CHEMISTRY |
| NARAYANA | COMREHENSION |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
Several short-lived radioactive species have been used to determine the age of wood or animal fossils. One of the most intresting substance is `""_(6)C""^(14)`(half-life fossils, etc.). Carbon-14 is produced by the bombardment of nitrogen atoms present in the upper atmosphere with neutrons (from cosmic rays).
`""_(7)N""^(14)+""_(0)n""^(1)to""_(6)C""^(14)+""_(1)H""_(1)`
Thus carbon-14 is oxidised, to `CO""_(2)` and eventually lingested by land animals. The death of plants or animals put an end to the intake of `C""_(14)` from the atmosphere. After this the amount of `C""_(14)` in the dead tissues starts decreasing due to its disintegration as per the following reaction :
`""_(6)C""^(14)to""_(7)N""^(14)+""_(-1)beta""^(0)`
The `C""^(14)` isotope enters the biosphjere when carbon dioxide is taken up in plant photosynthesis. Plants are eaten by animals, which exhale `C""^(14)` as `CO""_(2)`. Eventually, `C""^(14)` participates in many aspects of carbon cycle. The `C""^(14)` lost by radioactive decay-replenishment process, a dynamic rquillibrium is established whereby the ratio of `C""^(14)` to `C""^(12)` remains constant in living matter. But when an individual plant or an animal dies, the `C""^(14)` isotpe inn it is no longer replenished, so the ratio decreases as `C""^(14)` decays. So, ther number `C""^(14)` nuclei after time t (after the death of living matter) would be less than in a livingthe following formula, `t""_(1//2)=0.693`/?
The intensity of the cosmic rays have remain the same for 30,000 years. But since some years changes in this are observed due to excessive burning of fossil fuel and nuclear test?
Why do we use the carbon dating to calculate the age of the fossil?
View SolutionSeveral short-lived radioactive species have been used to determine the age of wood or animal fossils. One of the most intresting substance is `""_(6)C""^(14)`(half-life fossils, etc.). Carbon-14 is produced by the bombardment of nitrogen atoms present in the upper atmosphere with neutrons (from cosmic rays).
`""_(7)N""^(14)+""_(0)n""^(1)to""_(6)C""^(14)+""_(1)H""_(1)`
Thus carbon-14 is oxidised, to `CO""_(2)` and eventually lingested by land animals. The death of plants or animals put an end to the intake of `C""_(14)` from the atmosphere. After this the amount of `C""_(14)` in the dead tissues starts decreasing due to its disintegration as per the following reaction :
`""_(6)C""^(14)to""_(7)N""^(14)+""_(-1)beta""^(0)`
The `C""^(14)` isotope enters the biosphjere when carbon dioxide is taken up in plant photosynthesis. Plants are eaten by animals, which exhale `C""^(14)` as `CO""_(2)`. Eventually, `C""^(14)` participates in many aspects of carbon cycle. The `C""^(14)` lost by radioactive decay-replenishment process, a dynamic rquillibrium is established whereby the ratio of `C""^(14)` to `C""^(12)` remains constant in living matter. But when an individual plant or an animal dies, the `C""^(14)` isotpe inn it is no longer replenished, so the ratio decreases as `C""^(14)` decays. So, ther number `C""^(14)` nuclei after time t (after the death of living matter) would be less than in a livingthe following formula, `t""_(1//2)=0.693`/?
The intensity of the cosmic rays have remain the same for 30,000 years. But since some years changes in this are observed due to excessive burning of fossil fuel and nuclear test?
What should be the age of the fossil meaningful determination of its age?
View SolutionSeveral short-lived radioactive species have been used to determine the age of wood or animal fossils. One of the most intresting substance is `""_(6)C""^(14)`(half-life fossils, etc.). Carbon-14 is produced by the bombardment of nitrogen atoms present in the upper atmosphere with neutrons (from cosmic rays).
`""_(7)N""^(14)+""_(0)n""^(1)to""_(6)C""^(14)+""_(1)H""_(1)`
Thus carbon-14 is oxidised, to `CO""_(2)` and eventually lingested by land animals. The death of plants or animals put an end to the intake of `C""_(14)` from the atmosphere. After this the amount of `C""_(14)` in the dead tissues starts decreasing due to its disintegration as per the following reaction :
`""_(6)C""^(14)to""_(7)N""^(14)+""_(-1)beta""^(0)`
The `C""^(14)` isotope enters the biosphjere when carbon dioxide is taken up in plant photosynthesis. Plants are eaten by animals, which exhale `C""^(14)` as `CO""_(2)`. Eventually, `C""^(14)` participates in many aspects of carbon cycle. The `C""^(14)` lost by radioactive decay-replenishment process, a dynamic rquillibrium is established whereby the ratio of `C""^(14)` to `C""^(12)` remains constant in living matter. But when an individual plant or an animal dies, the `C""^(14)` isotpe inn it is no longer replenished, so the ratio decreases as `C""^(14)` decays. So, ther number `C""^(14)` nuclei after time t (after the death of living matter) would be less than in a livingthe following formula, `t""_(1//2)=0.693`/?
The intensity of the cosmic rays have remain the same for 30,000 years. But since some years changes in this are observed due to excessive burning of fossil fuel and nuclear test?
A nuclear explosion has taken place leading to increase in concentration of `C""^(14)` in nearby areas. `C""^(14)` concentration is `C""_(1)` in nearly areas and `C""_(2)` in areas far away. If the age of the fossil is determined to be `T""_(1)` and `T""_(2)` at the respective places then
View SolutionRadioactive disintegration is a first order reaction and it's rate depends only upon the nature of nucleus and does not depend upon external factors like temoperature an pressure. The rate of radioactive disintigration (Activity) is respresented as `(-d(N))/(dt)=lambdaN`
Where `lambda`=decay consatant, N= number of nuclei at time t, `N""_(0)`=initial no. of nucleei. The above equation after integration can be represented as
`lamda=2.303/tlog.(N""_(0))/(N)`
Half-life period of `U""^(237)` is `2.5xx10""^(5)` years. In how much time will the amount of `U""^(237)` remaining be only 25% of the original amount?
View SolutionRadioactive disintegration is a first order reaction and it's rate depends only upon the nature of nucleus and does not depend upon external factors like temoperature an pressure. The rate of radioactive disintigration (Activity) is respresented as `(-d(N))/(dt)=lambdaN`
Where `lambda`=decay consatant, N= number of nuclei at time t, `N""_(0)`=initial no. of nucleei. The above equation after integration can be represented as
`lamda=2.303/tlog.(N""_(0))/(N)`
Calculate the half-life period of a radioactive element which remains only 1/16 of it's original amount in 4740 years:
View SolutionRadioactive disintegration is a first order reaction and it's rate depends only upon the nature of nucleus and does not depend upon external factors like temoperature an pressure. The rate of radioactive disintigration (Activity) is respresented as `(-d(N))/(dt)=lambdaN`
Where `lambda`=decay consatant, N= number of nuclei at time t, `N""_(0)`=initial no. of nucleei. The above equation after integration can be represented as
`lamda=2.303/tlog.(N""_(0))/(N)`
What is the activity in Ci(curie) of 1.0 mole of plutonium-239?
View SolutionTwo substances A and B are present such that `[A_(0)]=4[B_(0]` and half-life of A is 5 minutes and that of B is 15 minutes. If they start decaying at the same time following first order kinetics after how much time the concentration of both of them would be same ?
View SolutionThe nuclei of two radioactive isotopes of same substance `A^(236)` and `A^(234)` are present in the ratio of `4:1` in an ore obtained from some other planet. Their half lives are `30min` and `60min` respectively. Both isotopes are alpha emitters and the activity of the isotope with half-life `30min` is `10^(6)dps`. Calculate after how much time their activites will become identical. Also calculate the time required to bring the ratio of their atoms to `1:1`.
View SolutionIn addition to the popular fusion reaction we come across, a second process called the carbon-nitrogen cycle occurs in the sun:
`""_(1)""^(1)H+""_(6)""^(12)Cto""_(0)""^(0)gamma+""_(7)""^(13)N` ,` ""_(13)""^(7)Nto""_(+1)""^(0)e+""_(13)""^(6)C`
`""_(1)""^(1)H+""_(6)""^(13)Cto""_(0)""^(0)gamma+""_(7)""^(14)N` ,`""_(1)""^(1)H+ ""_(7)""^(14)Nto""_(0)""^(0)gamma+""_(8)""^(15)O`
`""_(8)""^(15)Oto""_(+1)""^(0)e+""_(7)""^(15)N, ""_(1)""^(1)H+""_(7)""^(15)Nto""_(6)""^(12)C+""_(2)""^(4)He+""_(0)""^(0)gamma`
`4""_(1)""^(1)Hto""_(2)""^(4)He+2""_(+1)""^(0)e`
The catalyst oin the process is
View SolutionIn addition to the popular fusion reaction we come across, a second process called the carbon-nitrogen cycle occurs in the sun:
`""_(1)""^(1)H+""_(6)""^(12)Cto""_(0)""^(0)gamma+""_(7)""^(13)N` ,` ""_(13)""^(7)Nto""_(+1)""^(0)e+""_(13)""^(6)C`
`""_(1)""^(1)H+""_(6)""^(13)Cto""_(0)""^(0)gamma+""_(7)""^(14)N` ,`""_(1)""^(1)H+ ""_(7)""^(14)Nto""_(0)""^(0)gamma+""_(8)""^(15)O`
`""_(8)""^(15)Oto""_(+1)""^(0)e+""_(7)""^(15)N, ""_(1)""^(1)H+""_(7)""^(15)Nto""_(6)""^(12)C+""_(2)""^(4)He+""_(0)""^(0)gamma`
`4""_(1)""^(1)Hto""_(2)""^(4)He+2""_(+1)""^(0)e`
`""_(ss)Ra""^(226)tox+""_(2)He""^(4)` The product x belongs to the group of
View SolutionIn addition to the popular fusion reaction we come across, a second process called the carbon-nitrogen cycle occurs in the sun:
`""_(1)""^(1)H+""_(6)""^(12)Cto""_(0)""^(0)gamma+""_(7)""^(13)N` ,` ""_(13)""^(7)Nto""_(+1)""^(0)e+""_(13)""^(6)C`
`""_(1)""^(1)H+""_(6)""^(13)Cto""_(0)""^(0)gamma+""_(7)""^(14)N` ,`""_(1)""^(1)H+ ""_(7)""^(14)Nto""_(0)""^(0)gamma+""_(8)""^(15)O`
`""_(8)""^(15)Oto""_(+1)""^(0)e+""_(7)""^(15)N, ""_(1)""^(1)H+""_(7)""^(15)Nto""_(6)""^(12)C+""_(2)""^(4)He+""_(0)""^(0)gamma`
`4""_(1)""^(1)Hto""_(2)""^(4)He+2""_(+1)""^(0)e`
In the following nuclear reaction P and Q cannot be `""_(7)""^(15)N+Pto""_(7)""^(14)N+Q`
View SolutionUnstable nuclei attain stability through disintegration. The nuclear stability is related to neutron proton ratio (n/p). For stable nuclei n/p ratio lies close to unity for elements with low atomic numbers (20 or less) but it is more than 1 for nuclei having higher atomic numbers. Nuclei having n/p ratio either very high or low undergo nuclear transformation. when n/p ratio is higher than required for stabilioty, the nuclei have the tendency to emit `beta`-rays. While when n/p ratio is lower than required for stability, the nucleieither emits `alpha`-particles or a position or capture K-electron.
Unstable substance exhibit high radioactivity due to
View SolutionUnstable nuclei attain stability through disintegration. The nuclear stability is related to neutron proton ratio `(n//p)`. For stable nuclei `n//p` ratio lies close to unity for elements with low atmoic numbers (20 or less) but it is more than 1 for nuclei having higher atomic numbers. Nuclei having `n//p` ratio either very high or low undergo nuclear transformation. When `n//p` ratio is higher than required for stability, the nuclei have the tendency to emit `beta`-rays. while when `n//p` ratio is lower than required for stability, the nuclei either emits `alpha`-particles or a positron or capture `K`-electron.
`beta`-particle is emitted in radioactivity by
View SolutionUnstable nuclei attain stability through disintegration. The nuclear stability is related to neutron proton ratio `(n//p)`. For stable nuclei `n//p` ratio lies close to unity for elements with low atmoic numbers (20 or less) but it is more than 1 for nuclei having higher atomic numbers. Nuclei having `n//p` ratio either very high or low undergo nuclear transformation. When `n//p` ratio is higher than required for stability, the nuclei have the tendency to emit `beta`-rays. while when `n//p` ratio is lower than required for stability, the nuclei either emits `alpha`-particles or a positron or capture `K`-electron.
For reaction `._(92)M^(238) rarr ._(y)N^(x) + 2 ._(2)He^(4), ._(y)N^(x) rarr ._(B)L^(A) + 2 ._(-1)e^(0)`
The number of neutrons in the element `L` is
View SolutionUnstable nuclei attain stability through disintegration. The nuclear stability is related to neutron proton ratio (n/p). For stable nuclei n/p ratio lies close to unity for elements with low atomic numbers (20 or less) but it is more than 1 for nuclei having higher atomic numbers. Nuclei having n/p ratio either very high or low undergo nuclear transformation. when n/p ratio is higher than required for stabilioty, the nuclei have the tendency to emit `beta`-rays. While when n/p ratio is lower than required for stability, the nucleieither emits `alpha`-particles or a position or capture K-electron.
The order of radioactive disinigration is
View SolutionUranium (`""_(92)U""^(238)`) decayed to `""_(82)Pb""^(206)`. The process is `""_(92)U""^(238)underset(xalpha,ybeta)to.""_(82)Pb""^(206)`
`t""_(1//2)of U""^(238)=4.5xx10""^(9)` years
x and y in above decay series are
View SolutionUranium (`""_(92)U""^(238)`) decayed to `""_(82)Pb""^(206)`. The process is `""_(92)U""^(238)underset(xalpha,ybeta)to.""_(82)Pb""^(206)`
`t""_(1//2)of U""^(238)=4.5xx10""^(9)` years
A sample of rock from South America contains equal number of atoms of `U""^(238)` and `Pb""^(""^(206)`. The age of the rock will be
View SolutionUranium `._(92)U^(238)` decayed to `._(82)Pb^(206)`. They decay process is `._(92)U^(238) underset((x alpha, y beta))(rarr ._(82)Pb^(206))`
`t_(1//2)` of `U^(238) = 4.5 xx 10^(9)` years
Atomic mass of `U^(238)` is 238.125 amu. Its packing fraction will be
View SolutionUranium (`""_(92)U""^(238)`) decayed to `""_(82)Pb""^(206)`. The process is `""_(92)U""^(238)underset(xalpha,ybeta)to.""_(82)Pb""^(206)`
`t""_(1//2)of U""^(238)=4.5xx10""^(9)` years
The analysis of a rock shows the relative number of `U""^(238)` and `Pb""^(206)` atoms (Pb/U=0.25). The age of rock will be
View SolutionMonazite sample contains 9% `ThO""_(2)` and 0.35% `U""_(3)O""_(8).Pb""^(208)` and `Pb""^(206)` are the stable and products in the radioactive decay series of `Th""^(232)` and `U""^(238)` respectively. All the lead in mozaite is of radiogenic origin.
The isotopic ratio of `Pb""^(208)/Th""^(232)` was found to be 0.104. The half lives of Th and U are `1.41xx10""^(16)` years and `4.47xx10""^(9)` years respectively.
Select the information incorrect about `Th""^(232)`
View SolutionMonazite sample contains 9% `ThO""_(2)` and 0.35% `U""_(3)O""_(8).Pb""^(208)` and `Pb""^(206)` are the stable and products in the radioactive decay series of `Th""^(232)` and `U""^(238)` respectively. All the lead in mozaite is of radiogenic origin.
The isotopic ratio of `Pb""^(208)/Th""^(232)` was found to be 0.104. The half lives of Th and U are `1.41xx10""^(16)` years and `4.47xx10""^(9)` years respectively.
Estimated isotopic ratio of `Pb""^(206)//U""^(238)` in the monazite sample will be
View SolutionMonazite sample contains 9% `ThO""_(2)` and 0.35% `U""_(3)O""_(8).Pb""^(208)` and `Pb""^(206)` are the stable and products in the radioactive decay series of `Th""^(232)` and `U""^(238)` respectively. All the lead in mozaite is of radiogenic origin.
The isotopic ratio of `Pb""^(208)/Th""^(232)` was found to be 0.104. The half lives of Th and U are `1.41xx10""^(16)` years and `4.47xx10""^(9)` years respectively.
Select the information incorrect about `Th""^(232)`
View SolutionA small amount of solution containing a radioactive nucleide `A""^(x)` was administrated into the blood of a patient. The activity of the nucliede id `2xx10""^(3)`dps. Its half life is 15 hours. After 5 hours a sample of the blood drawn out from the patient. It,s activity was 16 dpm per mL.
What is the volume of the 'blood' in the patient? (Log(1.26)=0.1)
View SolutionA small amount of solution containing a radioactive nucleide `A""^(x)` was administrated into the blood of a patient. The activity of the nucliede id `2xx10""^(3)`dps. Its half life is 15 hours. After 5 hours a sample of the blood drawn out from the patient. It,s activity was 16 dpm per mL.
What is the activity of the sample after another 5 hours time?(L og1.59=0.2)
View SolutionA small amount of solution containing a radioactive nucleide `A""^(x)` was administrated into the blood of a patient. The activity of the nucliede id `2xx10""^(3)`dps. Its half life is 15 hours. After 5 hours a sample of the blood drawn out from the patient. It,s activity was 16 dpm per mL.
Radioactive nuclide `A""^(x)` decays by `beta-` emission (42%), `beta+`emission (58%) in the patient body.
Then half life value of `beta-`decary path is
View SolutionA small amount of solution containing a radioactive nucleide `A""^(x)` was administrated into the blood of a patient. The activity of the nucliede id `2xx10""^(3)`dps. Its half life is 15 hours. After 5 hours a sample of the blood drawn out from the patient. It,s activity was 16 dpm per mL.
At `A""^(x)`emits `alpha` ray. how many helium atoms present in hours?
View SolutionA small amount of solution containing a radioactive nucleide `A""^(x)` was administrated into the blood of a patient. The activity of the nucliede id `2xx10""^(3)`dps. Its half life is 15 hours. After 5 hours a sample of the blood drawn out from the patient. It,s activity was 16 dpm per mL.
If `A""^(x)` decays and finally `B""^(y)` unradioactive element obtained. After some time the sample contains %`A""^(x) and 10%B""^(y)` gm atoms present in it. The time taken for the attainment of conversion is
View SolutionA small amount of solution containing a radioactive nucleide `A""^(x)` was administrated into the blood of a patient. The activity of the nucliede id `2xx10""^(3)`dps. Its half life is 15 hours. After 5 hours a sample of the blood drawn out from the patient. It,s activity was 16 dpm per mL.
In the following graph, binding energy per nucleon is plotted against mass number (a). three elements `A_(1),A_(2)and A_(3)` are located in the graph. Select the false statement about the graph.

View SolutionA small amount of solution containing a radioactive nucleide `A""^(x)` was administrated into the blood of a patient. The activity of the nucliede id `2xx10""^(3)`dps. Its half life is 15 hours. After 5 hours a sample of the blood drawn out from the patient. It,s activity was 16 dpm per mL.
Binding energy per nucleon versus mass number for W,X,Y,Z are indicated on the curve.
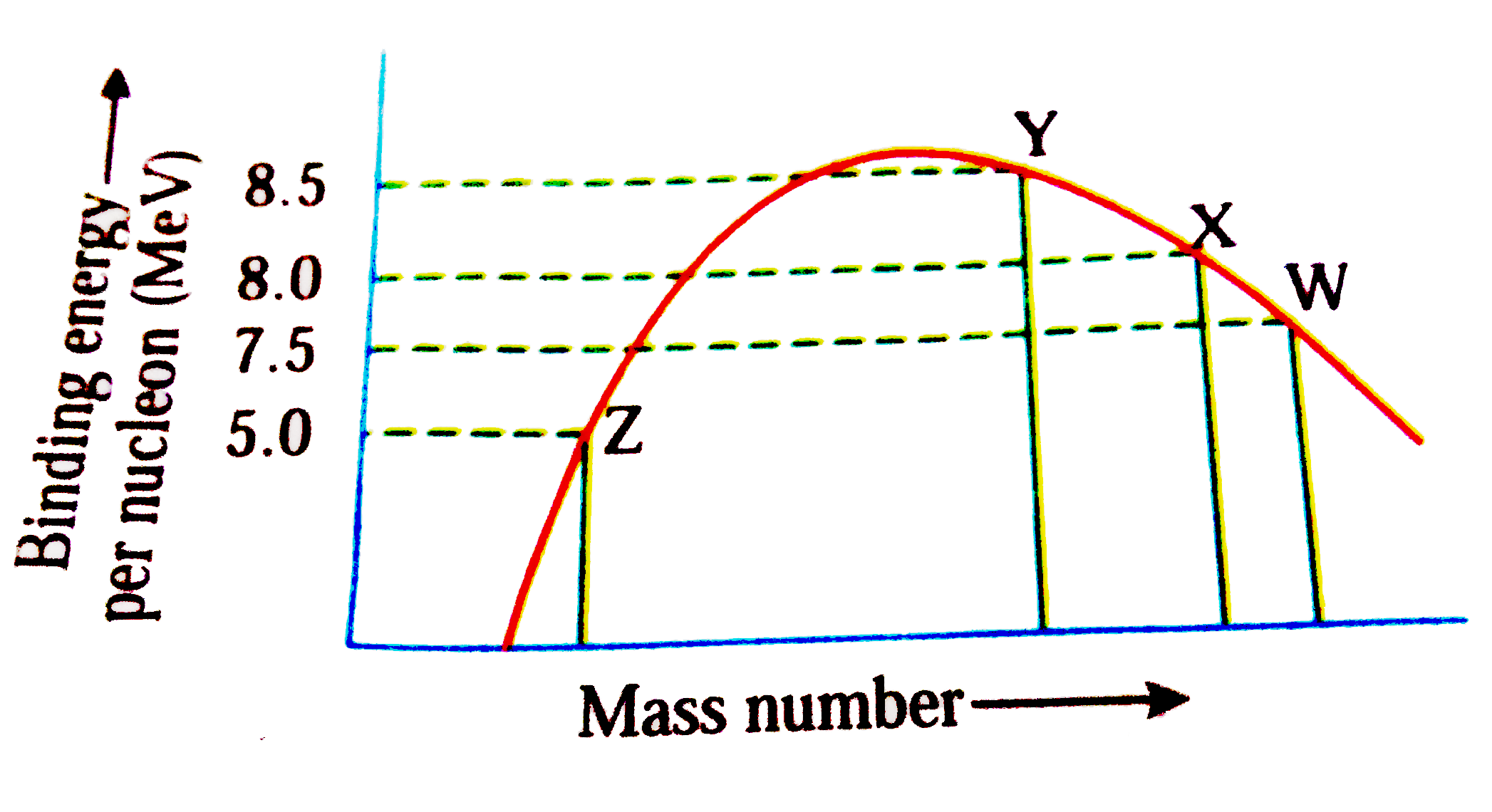
View Solution
COMREHENSION questions and complete solutions for chapter NUCLEAR CHEMISTRY of NARAYANA CHEMISTRY (HINGLISH) of Class 12