Complete Solutions to NCERT पाठ्यपुस्तक के प्रश्नोत्तर of chapter मापन में त्रुटियाँ, सार्थक अंक एवं विमाएँ of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | मापन में त्रुटियाँ, सार्थक अंक एवं विमाएँ |
| NAVBODH PARIKSHA SAAR | NCERT पाठ्यपुस्तक के प्रश्नोत्तर |
| Number Of Questions | 31 |
| Academic Year | 2023-24 |
कैलोरी, ऊष्मा या ऊर्जा का मात्रक है। एक पद्धति में 1 कैलोरी = 4.2 जूल, जहाँ 1 जूल = 1 किलोग्राम मीटर`""^(2)` सेकंड`""^(-2)` है। मानलो दूसरी पद्धति में द्रव्यमान का मात्रक `alpha` किग्रा, लंबाई का मात्रक `beta` मीटर तथा समय का मात्रक `gamma` सेकंड है। सिद्ध कीजिए कि नई पद्धति में 1 कैलोरी का मान `4.2 alpha^(-1)beta^(-2)gamma^(2)` होगा।
09:08View Solutionइस कथन की स्पष्ट व्याख्या कीजिए-
"तुलना के मानक का विशेष उल्लेख किये बिना किसी विमीय राशि को बड़ा या छोटा कहना अर्थहीन है।" इसे ध्यान में रखते हुए नीचे दिये गये कथनों को जहाँ कहीं भी आवश्यक हो, दूसरे शब्दों में व्यक्त कीजिए-
(a) परमाणु बहुत छोटे पिंड होते हैं।
(b) जेट वायुयान अत्यधिक बहुत ही अधिक है।
(c) बृहस्पति का द्रव्यमान बहुत ही अधिक है।
(d) इस कमरे के अंदर वायु में अणुओं की संख्या अधिक है।
(e) प्रोटॉन, इलेक्ट्रॉन से बहुत भरी होता है।
(f) ध्वनि की गति प्रकाश की गति से बहुत कम होती है।04:46View Solutionलंबाई का एक नया मात्रक इस प्रकार चुना जाता है कि निर्वात में प्रकाश की चाल एक है। यदि प्रकाश को सूर्य से पृथ्वी तक आने में 8 min और 20s लगते हों तो सूर्य और पृथ्वी के बीच की दूरी नये मात्रक में क्या होगी?
03:40View Solutionलंबाई नापने के लिए निम्नलिखित में से कौन-सा सबसे परिशुद्ध यंत्र है -
(a) एक वर्नियर कैलीपर्स जिसके वर्नियर पैमाने पर 20 विभाजन हैं?
(b) एक स्क्रुगेज जिसका चूड़ी अंतराल 1 mm तथा पैमाने पर 100 विभाजन है?
(c ) कोई प्रकाशिक यंत्र जो प्रकाश के तरंगदैर्ध्य की सीमा के अंदर लम्बाई माप सकता है?05:15View Solutionएक विद्यार्थी 100 आवर्धक क्षमता वाले सुक्ष्मदर्शी की सहायता से मानव बाल की मोटाई ज्ञात करता है। वह 20 प्रेक्षण लेता है और पता है कि सुक्ष्मदर्शी के दृष्टि क्षेत्र में बाल की औसत मोटाई 3.5 mm है। बताइये कि बाल की वास्तविक मोटाई क्या होगी?
01:44View Solutionनिम्नलिखित के उत्त्तर दीजिए-
(a) आपको एक धारा और मीटर पैमाना दिया जाता है| आप धागे के व्यास का अनुमान किस प्रकार लगाएंगे?
(b) एक शुक्रगेज का चूड़ी अंतराल 1.0 mm है और उसके वृतीय पैमाने पर 200 विभाजन है| क्या आप सोचते है की वृतीय पैमाने पर विभाज्यों की संख्या स्वेच्छा से बड़ा देने पर स्कूगेज की यथार्थता में वृद्धि करना सम्भव है?
( c) वर्नियर कैलिपर्स द्वारा पीतल की किसी पतली चढ़ का व्यास मापा जाना है| केवल 5 मापनों के सम्मुच्य की तुलना में व्यास के 100 मापनों के सम्मुच्य के द्वारा अधिक विश्वसनीय अनुमान प्राप्त होने की सम्भावना क्यों है?10:24View Solution35 mm स्लाइड पर एक मकान का फोटोग्राप 1.75 `cm^(2)` स्थान घेरता है| स्लाइड को स्क्रीन पर प्रोजेक्ट किया जाता है, जहाँ पर मकान का क्षेत्रफल `1.55 m^(2)` प्राप्त होता है| प्रोजेक्टर का रेखीय आवर्धन कितना होगा?
03:12View Solutionनिम्नलिखित में सार्थक अंकों की संख्या लिखिए-
(i) `0.007 m^(2)`, (ii) `2.64 xx 10^(24) kg`, (iii) `0.2370 g cm^(-3)`, (iv) `6.320 J`, (v) `6.032 Nm^(-2)`, (vi) `0.0006032 m^(2)`02:49View Solutionएक आयतकार वस्तु की लम्बाई, चौड़ाई और ऊंचाई क्रमश: `4.234 m, 1.005 m` और `2.01 cm` है| सही सार्थक अंकों में वस्तु का सम्पूर्ण पृष्ट तथा आयतन ज्ञात कीजिए|
07:46View Solutionएक पंसारी की तुला द्वारा मापे गए डिब्बे का द्रव्यमान 2.3 kg है| सोने के दो टुकड़े, जिसके द्रव्यमान 20.15 g व् 20.17 g है,डिब्बे में दाल दिए जाते है| निम्न का परिकलन कीजिए-
(i) डिब्बे का कुल द्रव्यमान, (ii) उचित सार्थक अंकों तक टुकड़े के द्रव्यमानों में अंतर|03:51View Solutionएक भौतिक राशि p निम्नलिखित समीकरण से प्रदर्शित की जाती है-
`P=(a^(3)b^(2))/(sqrt(c).d)`
यदि a,b,c और d की माप में प्रतिशत त्रुटियाँ क्रमश: `1%, 3%, 4%` व 2 % हो तो भौतिक राशि P की माप में प्रतिशत त्रुटि ज्ञात कीजिए| यदि P का मान उपर्युक्त समीकरण से 3.763 आता हो, तो उचित सार्थक अंकों में P का मान क्या होगा?04:03View Solutionकिसी पुस्तक में जिसकी छपाई में अनेक त्रुटियाँ है, एक सरल आवर्त गति कर रहे कण के विस्थापन के चार विभिन्न सूत्र दिए गए है-
(i) `y=a sin (2pit)/T`,
(ii) `y= a sin vt`
(iii) `y=a/T sin t/a`,
(iv) `y=(asqrt(2))(sin (2pit)/T + cos (2pit)/T)`
जहाँ a = कण का अधिकतम विस्थापन , v=कण की चाल तथा T=गति का आवर्तकाल है| विमीय विश्लेषण के आधार पर ज्ञात कीजिए की कौन-सा सूत्र गलत है?05:30View Solutionभौतिक का एक प्रसिद्द सम्बन्ध किसी कण के चल द्रव्यमान (moving mass)m, विराम द्रव्यमान (rest mass) `m_(o)`, इसकी चाल v ओर प्रकाश की चाल c के बीच है| (यह सम्बन्ध सबसे पहले अल्वर्ट आइंस्टाइन के विशेष आपेक्षित के सिद्धांत के परिणामस्वरूप उत्पन्न हुआ था| कोई छात्र इस सम्बन्ध को लगभग सही याद करता है लेकिन स्तिथरांक c को भूल जाता है| वह लिखता है-
`m=m_(0)/sqrt(1-v^(2))` , अनुमान लगाइये की c कहाँ लगेगा?02:57View Solutionहाइड्रोजन परमाणु की त्रिज्या `0.5 Å`है| एक हाइड्रोजन परमाणु के तथा 1 मोल हाइड्रोजन के आयतन की परिणाम की कोटि `m^(3)` में ज्ञात कीजिए|
04:27View Solutionकिसी आदर्श गैस का एक मोल (ग्राम अणुक) मानक ताप तथा दाब पर 22.4 लीटर (ग्राम अणुक आयतन) घेरता है| हाइड्रोजन के ग्राम अणुक आयतन तथा उसके एक मोल के परमाणिवक का अनुपात क्या होगा? (हाइड्रोजन के अनु का आमाप लगभग `1Å` है) यह अनुपात इतना अधिक क्यों है?
03:30View Solutionइस सामान्य प्रेक्षण की स्पष्ट व्याख्या कीजिए: जब आप तेज गति से चलती हुई रेलगाइ की खिड़की से बाहर देखते है तो पास स्तिथ वस्तुएं जैसे -पेड़, मकान आदि होती है जबकि दूर स्तिथ वस्तुओं (वास्तव में, क्यूंकि आपको ज्ञात है की आप चल रहे है, इसलिए ये दूरस्थ वस्तुएं आपको अपने साथ चलती हुई प्रतीत होती है) स्थिर दिखाई देती है|
02:57View Solutionसमीपी तारों की दूरियां ज्ञात करने के लिए लंबन के सिद्धांत का प्रयोग किया जाता है| सूर्य के परितः अपनी कक्षा में छ: महीनों के अंतराल पर पृथ्वी की अपनी दो स्थानों को मिललने वाली आधार रेखा AB है अर्थात आधार रेखा पृथ्वी की कक्षा के व्यास = `3 xx 10^(11)m` के लगभग बराबर है| लेकिन, अधिक दूर है की इतनी लम्बी आधार रेखा होने पर भी वे चाप के केवल 1 '' सेकंड चाप का) की कोटि का लंबन प्रदर्शित करते है| खगोलीय पैमाने पर लम्बाई का सुविधाजनक मात्रक पारसेक है| यह किसी पिंड की यह दुरी है जो पृथ्वी से सूर्य की तक की दुरी के बराबर आधार रेखा के दो विपरीत किनारों से चाप के 1'' का लंबन प्रदर्शित करती है| मटीरों में एक पारसके कितना होता है?
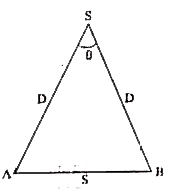 05:09View Solution
05:09View Solutionहमारे सौर परिवार से निकटतम तारा 4.29 प्रकाश वर्ध दूर है| पारसेक में यह दुरी कितनी है? यह तारा (एल्फासेंटरी नामक) तब कितना लंबन प्रदर्शित करेगा जब इसे सूर्य के पारित अपनी कक्षा में पृथ्वी के दो स्थानों से, जो छ: महीने के अंतराल पर है, देखा जायेगा?
02:55View Solutionभौतिक राशियों का परिशुद्ध मापन विज्ञानं की आवश्यकताएं है| उदाहरण के लिए, किसी लड़ाकू जहाज की चल सुनिश्चित करने के लिए बहुत ही छोटे समय अंतरालों पर इसकी स्थिति का पता लगाने की कोई यथार्थ विधि होनी चाहिए| द्वितीय विश्व युद्ध में राडार की खोज के पीछे वास्तविक प्रयोजन यही था| आधुनिक विज्ञानं के उन भिन्न उदाहरणों को सोचिये जिनमे लम्बाई, समय, द्रव्यमान आदि के परिशुद्ध मापन की आवश्यकता होती है| अन्य जिस किसी विषय में भी आप बता सकते है परिशुद्धता की मात्रात्मक धारणा दीजिये|
02:50View Solutionजिस प्रकार विज्ञानं में परिशुद्ध मापन आवश्यक है, उसी प्रकार अलप विकसित विचारों तथा सामान्य प्रेक्षणों को उपयोग करने वाली राशियों के स्थूल आकलन कर सकना भी उतना ही महत्वपूर्ण है| उन उपायों को सोचिये जिनके द्वारा आप निम्नलिखित का अनुमान लगा सकते है, (जहाँ अनुमान लगाना कठिन है वहा राशि की उपरिसीमा पता लगाने का प्रयास कीजिए)
(a) मानसून की अवधि में भारत के ऊपर वर्षाधारी मेघों का कुल द्रव्यमान (b) किसी हाथी का द्रव्यमान| ( c ) किसी तूफ़ान की अवधि में वायु की चाल| ( d) आपके सर में बालों की संख्या| (e) आपकी कक्षा के कमरे में वायु के अणुओं की संख्या|05:05View Solutionसूर्य एक ऊष्मा प्लाज्मा (आयनीकृत पदार्थ) है, जिसके आंतरिक करोड़ का ताप `10^(7) K` से अधिक है| इसके बहम पृष्ट का ताप 6000 K है| इतने अधिक ताप पर कोई भी पदार्थ ठोस या तरल प्रावस्था में नहीं रह सकता| आपको सूर्य का घनत्व किस परिसर में होने की आशा है? क्या यह ठोसों, तरलों या गैसों के घनत्व के परिसर में है? क्या आपका अनुमान सही है, इसकी जांच आप निम्नलिखित आकड़ों के ादहर पर कर सकते है?
सूर्य का द्रव्यमान `=2.0 xx 10^(30)kg`
सूर्य की त्रिज्या `=7.0 xx 10^(8)`m.03:25View Solutionजब बृहस्पति ग्रह पृथ्वी से 8247 लाख किलोमीटर दूर होता है, तो इसके व्यास का कोणीय माप `35.72''` का चाप है? बृहस्पति का व्यास कितना होगा?
02:54View Solutionवर्षों के समय कोई व्यक्ति चाल v के साथ तेजी से चला जा रहा है| उसे अपने छाते को टेड़ा करके ऊथ्व के साथ 0 कोण बनाना पड़ता है| कोई विघार्थी कोण 0 ओर v के बीच निम्नलिखित संबंध व्युतपन्न करता है-
`tan theta = v`
ओर वह इस सम्बन्ध के औचित्य की सीमा पता लगता है| जैसा की आशा की जाती है यिद `v lt 0` तो `0 lt o` (हम यह मान रहे है की तेज वायु नहीं चल रही है ओर किसी खड़े व्यक्ति के लिए वर्षा उध्र्वाधतः पड़ रही है) क्या आप सोचते है की यह सम्बन्ध सही हो सकता है? यदि ऐसा नहीं है तो सही सम्बन्ध का अनुमान लगाइये|06:38View Solutionयह दावा किया जाता है की यदि बिना किसी बाधा के 100 वर्षों तक दो सीजियम घाटियों को चलने दिया जाये तो उनके समयों में केवल 0.025 का अंतर् हो सकता है| मानक सीजियम घडी द्वारा 1s के समय अंतराल को मापने में यथार्थता के लिए इसका क्या अभिप्राय है?
03:33View Solutionएक सोडियम परमाणु का साइज `2.5 Å` है| उसका माध्य घनत्व ज्ञात कीजिए| इस घनत्व की क्रिस्टलीय प्रावस्था में सोडियम के घनत्व `970 kmg^(-3)` के साथ तुलना कीजिए| क्या इन दोनों घनत्वों के परिणाम की कोटियाँ समान है? यदि हाँ, तो क्यों?
04:00View Solutionनाभिकीय साइज लगभग निम्न मुलानुपाती सूत्र (Empirical formula) का पालन करता है-
`r=r_(0)a^(1//3)`
जहाँ r नाभिका की त्रिजुया तथा A इसकी द्रव्यमान संख्या है| `r_(0)` एक नियतांक है जो लगभग 1.2 f के बराबर है| सिद्ध कीजिए की विभिन्न नाभिकों के लिए नाभिकीय द्रव्यमान घनत्व लगभग स्थिर है| सोडियम नाभिक के द्रव्यमान घनत्व का परिकलन कीजिए| सोडियम परमाणु का माध्य द्रव्यमान घनत्व `600 kgm^(-3)` है|05:29View Solutionलेसर (LASER) प्रकाश के अत्यधिक तीव्र, एकवर्णिक तथा एक दिशा किरण पुंज का स्त्रोत है| लेसर के इन गुणों का लम्बी दूरियां मापने में उपयोग किया जाता है| लेसर को प्रकाश के स्त्रोत के रूप में उपयोग करते हुए पहले ही चन्द्रमा की पृथ्वी से दुरी परिशुद्धता से ज्ञात की जा चुकी है|
लेसर प्रकाश को पृथ्वी से चन्द्रमा तक जाने ओर चन्द्रमा की सतह से टकराकर पृथ्वी तक आने में 2.56 s का समय लगता है| पृथ्वी से चन्द्रमा की दुरी ज्ञात कीजिए|01:43View Solutionजल के नीचे वस्तुओं को ढूढ़ने व उनके स्थान का पता लगाने के लिए सोनार (SONAR) में पराश्रव्य तरंगों का उपयोग किया जाता है| एक पनडुब्बी सोनार से सुसज्जित है| इसके द्वारा उत्सर्जित अन्वेषी तरंग शत्रु की पनडुब्बी से परावर्तित इसकी प्रतिध्वनि के बीच काल विलम्ब `77.0s` है | शत्रु की पनडुब्बी कितनी दूर है? (जल में ध्विनि की चाल `=1450 ms^(-1)`)
02:01View Solutionहमारे विश्व में आधुनिक खगोलविदों द्वारा खोजे गए सर्वाधिक दूरस्थ पिंड इतने दूर है की उनके द्वारा उत्सर्जित प्रकाश को पृथ्वी तक पहुंचने में अरबों वर्ष लगते है| इन पिंडों (जिन्हे कवासर Quasar) कहा जाता है के कई रहस्मय लक्षण है जिनकी अभी तक संतोषजनक व्याख्या नहीं की जा स्की है| किसी ऐसे कवासर से उत्सर्जित प्रकाश को पृथ्वी तक पहुंचने में 300 करोड़ वर्ष लगते है| कवासर की पृथ्वी से दुरी कितनी होगी?
03:30View Solutionयह एक विख्यात तथ्य है की पूर्ण सूर्यग्रहण की अवधि में चन्द्रमा की चक्रिका सूर्य की चक्रिका को पूर्णतः ढक लेती है| चन्द्रमा का लगभग व्यास ज्ञात कीजिए|
दिया है- सूर्य कोणीय व्यास `1920''`, पृथ्वी से चन्द्रमा की दुरी `=3.84 xx 10^(8)m`, पृथ्वी की सूर्य से दुरी `=1.496 xx 10^(11)m`.04:22View Solutionइस शताब्दी के एक महान भौतिकविद (पी.ए.एम्. डीरेक Dirac) प्रकृति के मूल स्थितरकों (नियतांकों) के आंकिक मानों के साथ क्रीड़ा में अनंत लेते थे| इससे उन्होंने एक बहुत ही रोचक प्रेक्षण किया| परमाण्वीय भौतिकी के मूल नियतांकों G ) से उन्हें पता लगा की वे ऐसे संख्या पर पहुँच गए है जिसकी वीमा समय की विमा है| साथ ही यह के बहुत बड़ी संख्या थी ओर इसका परिणाम विश्व की वर्तमान आकलित आयु (~1500 करोड़ वर्ष) के करीब है| इस पुस्तक में दी मूल नियतांकों की सारणी के आधार पर यह देखने का प्रयास कीजिए की क्या आप भी यह संख्या (या ओर कोई अन्य रोचक संख्या जिसे आप सोच सकते है) बना सकते है? यदि विश्व की आयु तथा इस संख्या में समानता महत्पूर्ण है तो मूल नियतांकों की स्तिथरता किस प्रकार प्रभावित होगी?
03:56View Solution
NCERT पाठ्यपुस्तक के प्रश्नोत्तर questions and complete solutions for chapter मापन में त्रुटियाँ, सार्थक अंक एवं विमाएँ of NAVBODH PHYSICS (HINDI) of Class 12
All Exercises from NAVBODH PARIKSHA SAAR Class 12 PHYSICS मापन में त्रुटियाँ, सार्थक अंक एवं विमाएँ
- NCERT पाठ्यपुस्तक के प्रश्नोत्तर
- NCERT पाठ्यपुस्तक के प्रश्नोत्तर (रिक्त स्थान को मात्रकों के उचित परिवर्तन द्वारा भरिए)
- NCERT पाठ्यपुस्तक के प्रश्नोत्तर (रिक्त स्थान भरिए)
- अभ्यासार्थ प्रश्न ( रिक्त स्थानों की पूर्ति कीजिए - )
- अभ्यासार्थ प्रश्न (अति लघु उत्तरीय प्रश्न/एक शब्द/ एक वाक्य)
- अभ्यासार्थ प्रश्न (उचित संबंध जोड़िए - )
- अभ्यासार्थ प्रश्न (दीर्घ उत्तरीय प्रश्न )
- अभ्यासार्थ प्रश्न (बहुविकल्पीय प्रश्न )
- अभ्यासार्थ प्रश्न (लघु उत्तरीय प्रश्न )
- अभ्यासार्थ प्रश्न (सत्य/असत्य प्रश्न )
- आंकिक उदाहरण
- आंकिक उदाहरण प्लस
- आंकिक प्रश्न
- उदाहरण
- तथ्यात्मक प्रश्न
- बहुविकल्पीय प्रश्न
- बोधात्मक प्रश्न
- बोधात्मक प्रश्न प्लस
