Complete Solutions to प्रश्नावली 1.4 of chapter संबंध एवं फलन of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | संबंध एवं फलन |
| NCERT HINDI | प्रश्नावली 1.4 |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
निर्धारित कीजिए कि क्या निम्नलिखित प्रकार से परिभाषित प्रत्येक संक्रिया * से एक द्विआधारी संक्रिया प्राप्त होती है या नहीं। उस दशा में जब * एक द्विआधारी संक्रिया नहीं है, औचित्य भी बतलाइए।
(i) `Z^(+)` में, a * b = a - b द्वारा परिभाषित संक्रिया *.
(ii) `Z^(+)` में, a * b = ab द्वारा परिभाषित संक्रिया *
(iii) R में, संक्रिया *, a *b = `ab^(2)` द्वारा परिभाषित
. (iv) `Z^(+)` में, संक्रिया *, a * b = |a-b| द्वारा परिभाषित
(v) `Z^(+)` में, संक्रिया *, a * b= a द्वारा परिभाषित
View Solutionनिम्नलिखित परिभाषित प्रत्येक द्विआधारी संक्रिया * के लिए निर्धारित कीजिए कि क्या * द्विआधारी क्रमविनिमय है तथा क्या * साहचर्य है।
(i) Z,मे a * b = a-b द्वारा परिभाषित
(ii) Q मे, a*b = ab + 1 द्वारा परिभाषित
(iii) Q मे, `a**b = (ab)/(2)` द्वारा परिभाषित
(iv)`Z^(+)` मे`a**b= 2^(ab)` द्वारा परिभाषित
(v) `Z^(+)` मे, `a**b = a^(b)` द्वारा परिभाषित
(vi)`R -{-1}` मे `a**b = (a)/(b+1)` द्वारा परिभाषित
View Solutionसमुच्चय {1, 2, 3, 4, 5} में `a^^b`= निम्नतम `{a,b}` द्वारा परिभाषित द्विआधारी संक्रिया पर विचार कीजिए। सक्रिया `^^` के लिए संक्रिया सारणी लिखिए
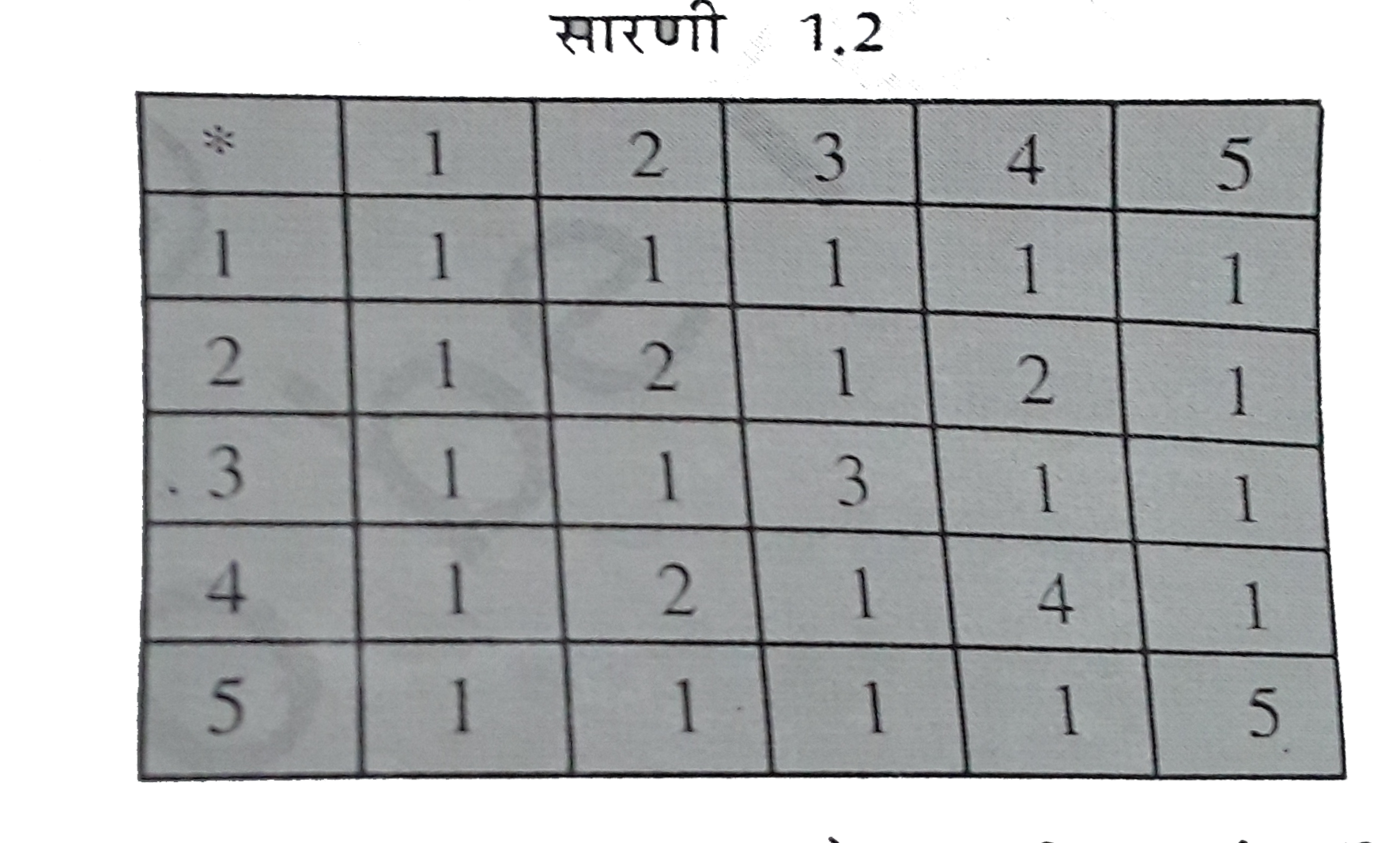
View Solutionसमुच्चय (1, 2, 3, 4, 5) में, निम्नलिखित सक्रिया सारणी (सारणी 1.2) द्वारा परिभाषित, द्विआधारी संक्रिया * पर विचार कीजिए तथा.
(i) (2 * 3) * 4 तथा 2 * (3 * 4 ) का परिकलन कीजिए।
(ii) क्या * क्रमविनिमेय है?
(iii) (2 * 3) * (4 * 5) का परिकलन कीजिए ।
(संकेत: निम्न सारणी का प्रयोग कीजिए।).
View Solutionमान लीजिए कि समुच्चय {1, 2, 3, 4, 5} में एक द्विआधारी संक्रिया *' ,a *' b = a तथा b का HCF द्वारा परिभषित है। क्या संक्रिया उपर्युक्त प्रश्न 4 में परिभाषित संक्रिया * के समान है? अपने उत्तर औचित्य भी बतलाइए।
View Solutionमान लीजिए कि Nमें एक द्विआधारी संक्रिया *,a*b =a तथा b का LCM द्वारा परिभाषित है। निम्नलिखित ज्ञात कीजिए:
(i) 5*7, 20 *16
(ii) क्या संक्रिया *क्रमविनिमेय है ?
(iii) क्या* साहचर्य है?
(iv) N में * का तत्समक्र अवयव ज्ञात कीजिए
(v) N के कौन से अवयव * संक्रिया के लिए व्युत्क्रमणीय है ?
View Solutionक्या समुच्चय {1, 2. 3. 4. 5) में a * b = a तथा b का LCM द्वारा परिभाषित * एक द्विआधारी संक्रिया है? अपने उत्तर का औचित्य भी बतलाइए।
View Solutionमाना कि N में `a **b = a ` तथा b का HCF , द्वारा परिभाषित एक द्विआधारी संक्रिया है। क्या `**` क्रमविनिमेय है ? क्या `**` साहचर्य है ? क्या N में इस द्विआधारी संक्रिया के तत्समक का आस्तित्व है ?
View Solutionमान लीजिए कि परिमेय संख्याओं के समुच्चय Q में निम्नलिखित प्रकार से परिभाषित * एक द्विआधारी संक्रिया है:
.
ज्ञात कीजिए कि इनमें से कौन सी संक्रियाएँ क्रमविनिमेय हैं और कौन सी साहचर्य हैं।
(i) a*b = a-b (ii) a*b `= a^(2) + b^(2)`
(iii) a*b = a+ ab (iv) a*b `= (a-b)^(2)`
(v) a*b `= (a^(b))/(4)` (vi) a*b `= ab^(2)`
View Solutionप्रश्न 9 में दी गयी संक्रियाओं में किसी का तत्समक हैं , वह बतलाइये
`i) a**b=a-b`
`ii) a**b=a^2+b^2`
`iii) a**b=a+ab`
`iv) a**b=(a-b)^2`
`v) a**b=a^b/4`
`i) a**b=ab^2`
View Solutionमाना कि `A = N xx N ` है तथा A में `(a , b ) ** (c , d ) = (a +c , b +d )` द्वारा परिभाषित एक द्विआधारी संक्रिया `**` है। सिद्ध कीजिए कि `**` क्रमविनिमेय तथा साहचर्य है। A में `**` का तत्समक अवयव यदि कोई है, तो ज्ञात कीजिए।
View Solutionबतलाइए कि क्या निम्नलिखित कथन सत्य हैं या असत्य है। औचित्य भी बतलाइए।
(i) समुच्चय N में किसी भी स्वेच्छ द्विआधारी संक्रिया * के लिए , `a**a=a, AA a in N`
(ii )यदि N में * एक क्रमविनिमेय द्विआधारी संक्रिया है, तो `a** (b**c) = (c**b) **a`
View Solution`a**b = a^(3) + b^(3)`प्रकार से परिभाषित N में एक द्विआधारी संक्रिया * पर विचार कीजिए। अब निम्नलिखित में से सही उत्तर का चयन कीजिए
(A) * साहचर्य तथा क्रमविनिमेय दोनों है
(B) * क्रमविनिमेय है किंतु साहचर्य नहीं है।
(C) * साहचर्य है किंतु क्रमविनिमेय नहीं है।
(D) * न तो क्रमविनिमेय है और न साहचर्य है
View Solution
प्रश्नावली 1.4 questions and complete solutions for chapter संबंध एवं फलन of NCERT गणित(HINDI) of Class 12