Complete Solutions to EXERCISE 5.8 of chapter CONTINUITY AND DIFFERENTIABILITY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | CONTINUITY AND DIFFERENTIABILITY |
| Mathematics | EXERCISE 5.8 |
| Number Of Questions | 6 |
| Academic Year | 2023-24 |
Examine the applicability of Mean Value Theorem for all three functions given in the above exercise 2.
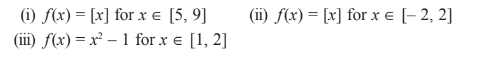
View SolutionVerify Mean Value Theorem, if `f(x)=x^2-4x-3` in the interval [a, b], where `a = 1 and b = 4`.
View SolutionVerify Mean Value Theorem, if `f(x)=x^3-5x^2-3x` in the interval [a, b], where `a = 1 and b = 3`. Find all `c in (1, 3)` for which `f^(prime)(c)=0`.
View SolutionExamine if Rolle's theorem is applicable to any of the following functions. Can you say something about the converse of Rolle's theorem from these example?
(i) `f(x)=[x]` for `x in [5,9]`
(ii) `f(x) = [x]` for `x in [-2,2]`
(iii) `f(x)=x^2-1` for `x in [1,2]`
View SolutionVerify Rolle's theorem for the function `f(x)=x^2+2x-8,``x in [-4,2]`.
View SolutionIf `f : [-5, 5] to R` is a differentiable function and if `f^(prime)(x)` does not vanish anywhere, then prove that `f(-5) ne f(5)`.
View Solution
EXERCISE 5.8 questions and complete solutions for chapter CONTINUITY AND DIFFERENTIABILITY of NCERT MATHEMATICS(HINGLISH) of Class 12