Complete Solutions to Exercise of chapter MOTION IN ONE DIMENSION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOTION IN ONE DIMENSION |
| NEET PREVIOUS YEAR | Exercise |
| Number Of Questions | 46 |
| Academic Year | 2023-24 |
Preeti reached the metro station and found that the escalator was not working. She walked up the stationary escalator in time `t_1`. On other days, if the remains stationary on the moving escalator, then the escalator takes her up in time `t_2`. The time taken by her to walk up on the moving escalator will be :
View SolutionIf the velocity of a particle is `v = At + Bt^2`, where `A` and `B` are constant, then the distance travelled by it between `1 s` and `2 s` is :
View SolutionTwo cars `P` and `Q` start from a point at the same time in a straight line and their position are represented by `x_p(t) = at + bt^2` and `x_Q (t) = ft - t^2`. At what time do the cars have the same velocity ?
View SolutionA particle of unit mass undergoes one-dimensional motion such that its velocity varies according to
`v(x) = beta x^(-2 n)`
where `beta` and `n` are constant and `x` is the position of the particle. The acceleration of the particle as a function of `x` is given by.
View SolutionIf Vectors `vec(A)= cos omega hat(i)+ sin omega hat(j)` and `vec(B)=(cos)(omegat)/(2)hat(i)+(sin)(omegat)/(2)hat(j)`are functions of time. Then the value of `t` at which they are orthogonal to each other is
View SolutionThe range R of projectile is same when its maximum heights are `h_(1) and h_(2)`. What is the relation between R, `h_(1) and h_(2)`?
View SolutionThe motion of a particle along a straight line is described by equation : `x = 8 + 12 t - t^3` where `x` is in metre and `t` in second. The retardation of the particle when its velocity becomes zero is.
View SolutionA boy standing at the top of a tower of `20 m`. Height drops a stone. Assuming `g = 10 ms^-2` towards north. The average acceleration of the body is.
View SolutionA body is moving with velocity `30 m//s` towards east. After `10 s` its velocity becomes `40 m//s` towards north. The average acceleration of the body is.
View SolutionA ball is droped from a high rise platform `t = 0` starting from rest. After `6 s` another ball is thrown downwards from the same platform with a speed `v`. The two balls meet at `t = 18 s`. What is the value of `v` ?
View SolutionA particle move a distance `x` in time `t` according to equation `x = (t + 5)^-1`. The acceleration of particle is alphaortional to.
View SolutionA particle starts its motion from rest under the action of a constant force. If the distance covered in first `10 s` is `s_1` and the covered in the first `20 s` is `s_2`, then.
View SolutionA bus is moving with a speed of `10 ms^-1` on a straight road. A scooterist wishes to overtake the bus in `10 s`. If the bus is at a distance of `1 km` from the scooterist with what speed should the scooterist chase the bus ?
View SolutionA particle moves in a straight line with a constant acceleration. It changes its velocity from `10 ms^-1` to `20 ms^-1` while passing through a distance `135 m` in `t` seconds. The value of `t` is.
View SolutionA particle shows distance-time curve as given in this figure. The maximum instantaneous velocity of the particle is around the point.
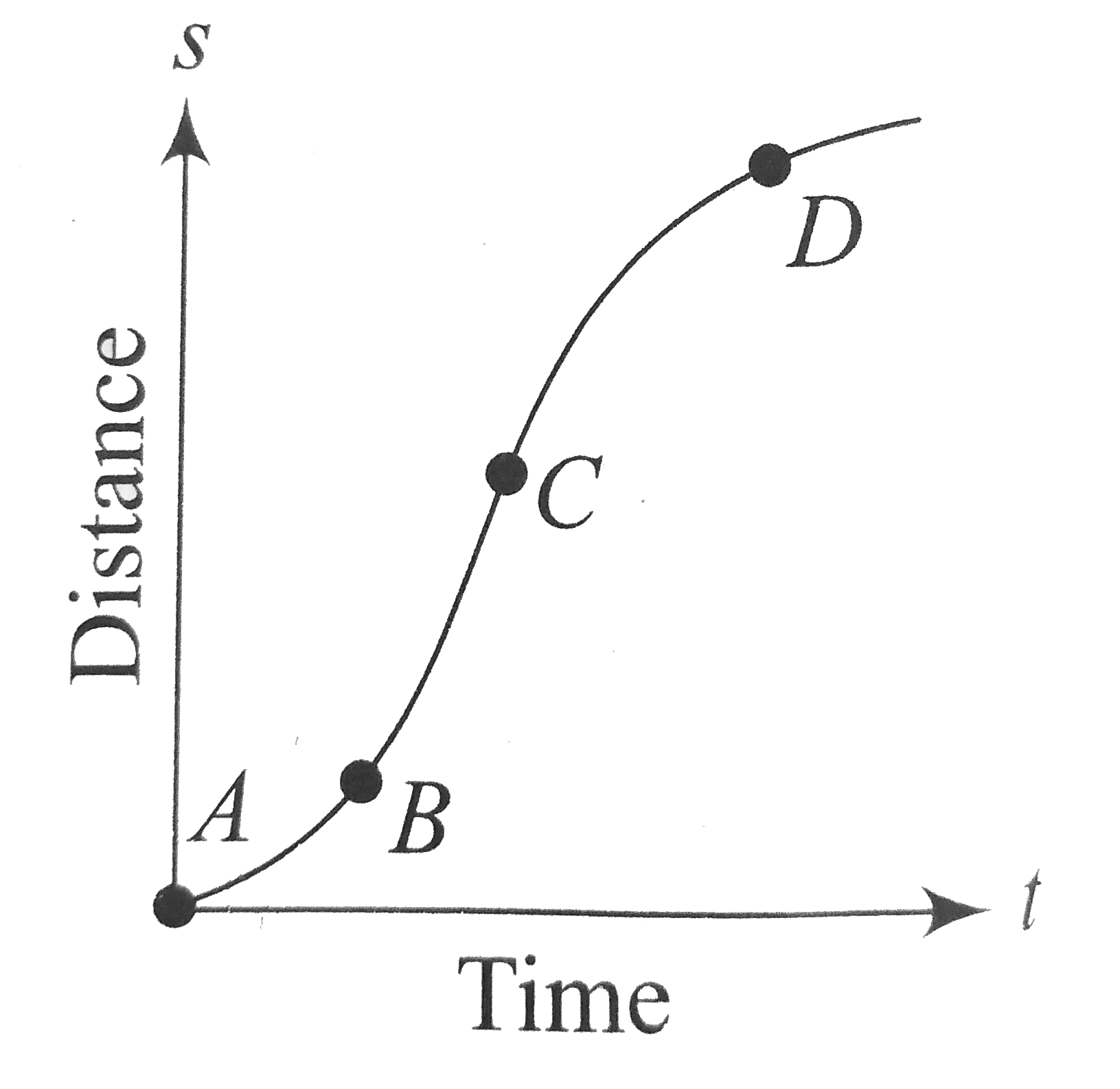 .
.
View SolutionThe distance travelled by a particle starting from rest and moving with an acceleration `(4)/(3) ms^-2`, in the third second is.
View SolutionA particle moving along x-axis has acceleration `f`, at time `t`, given by `f = f_0 (1 - (t)/(T))`, where `f_0` and `T` are constant.
The particle at `t = 0` has zero velocity. In the time interval between `t = 0` and the instant when `f = 0`, the particle's velocity `(v_x)` is :
View SolutionA car moves from `X` to `Y` with a uniform speed `v_u` and returns to `Y` with a uniform speed `v_d`. The average speed for this round trip is :
View SolutionThe position `x` of a particle with respect to time `t` along the x-axis is given by `x=9t^(2)-t^(3)` where `x` is in meter and `t` in second. What will be the position of this particle when it achieves maximum speed along the positive `x` direction
View SolutionTwo bodies `A` (of mass `1 kg`) and `B` (of mass `3 kg`) are dropped from heights of `16 m` and `25 m`. Respectively. The ratio of the time taken to reach the ground is :
View SolutionA particle moves along a straight line `OX`. At a time `t` (in seconds) the distance `x` (in metre) of the particle is given by `x = 40 +12 t - t^3`. How long would the particle travel before coming to rest ?
View SolutionThe displacement `x` of a particle varies with time `t` as `x = ae^(-alpha t) + be^(beta t)`. Where `a,b, alpha` and `beta` positive constant.
The velocity of the particle will.
View SolutionA man throws ball with the same speed vertically upwards one after the other at an interval of 2 seconds. What should be the speed of the throw so that more than two ball are in the sky at any time (Given `g=10(m)/(2^2)`)
View SolutionIf a ball is thrown vertically upwards with speed `u`, the distance covered during the last `t` second of its ascent is
View SolutionA stone is thrown vertically upwards. When stone is at a height half of its maximum height, its speed is `10 ms^-1` , then the maximum height attained by the stone is (`g= 10 ms^(-2)`)
View SolutionA particle moves along a straight line such that its displacement at any time t is given by `s = 3t^(3)+7t^(2)+14t + 5`. The acceleration of the particle at `t = 1s` is
View SolutionA car moving with a speed of `40 km//h` can be stopped by applying the brakes after at least 2 m. If the same car is moving with a speed of `80 km//h`, what is the minimum stopping distance?
View SolutionIf a car at rest, accelerates uniformly to a speed of `144 km//h` in `20s`, it covers a distance of
View SolutionThe position `x` of a particle varies with time `t` as `x=at^(2)-bt^(3)`. The acceleration at time `t` of the particle will be equal to zero, where (t) is equal to .`
View SolutionIf a ball is thrown vertically upwards with a velocity of `40m//s`, then velocity of the ball after `2s` will be `(g = 10m//s^(2))`
View SolutionThree different objects of masses `m_(1) , m_(2)` and `m_(2)` are allowed to fall from rest and from the same point `O` along three different frictionless paths. The speeds of three objects on reaching the ground will be:
View SolutionWater drops fall at regular intervals from a tap 5 m above the ground. The third drop is leaving the tap, the instant the first drop touches the ground. How far above the ground is the second drop at that instant. `(g = 10 ms^-2)`
View SolutionA body is thrown vertically upwards from the ground. It reaches a maximum height of `20 m` in `5s`. After what time it will reach the ground from its maximum height position ?
View SolutionA stone released with zero velocity from the top of a water, reaches the ground in 4s. The height of the tower is `(g = 10 m//s^(2))`
View SolutionA car accelerates from rest at a constant rate `alpha` for some time, after which it decelerates at a constant rate `beta,` to come to rest. If the total time elapsed is t seconds. Then evalute (a) the maximum velocity reached and (b) the total distance travelled.
View SolutionA particle moves along a staight line such that its displacement at any time t is given by `s=t^3-6t^2+3t+4m`. Find the velocity when the acceleration is 0.
View SolutionThe displacement-time graph of moving particle is shown below

The instantaneous velocity of the particle in negative at the point
View SolutionA body starts from rest, what is the ratio of the distance travelled by the body during the 4th and 3rd s?
View SolutionA train of `150 m` length is going toward north direction at a speed of `10 ms^-1`. A parrot flies at a speed of `5 ms^-1` toward south direction parallel to the railway track. The time taken by the parrot to cross the train is equal to.
View SolutionWhich of the following curves does not represent motion in one dimensions?
View SolutionA bus travelled the first one-third distance at a speed of `10 km//h`, the next one-third at `20 km//h` and the last one-third at `60 km//h`. The average speed of the bus is
View SolutionA car moves a distance of `200 m`. It covers the first-half of the distance at speed `40km//h` and the second-half of distance at speed `v km//h`. The average speed is `48km//h`. Find the value of v.
View SolutionA body dropped from top of a tower falls through ` 40 m` during the last two seconds of its fall. The height of tower in m is `( g= 10 m //s^2)`
View SolutionA car travels along a straight line for first half time with speed `40 km//h` and the second half time with speed `60 km//h`. Find the average speed of the car.
View SolutionFind the ratio of the distance moved by a free-falling body from rest in fourth and fifth seconds of its journey.
View SolutionA car is moving along a straight road with a uniform acceleration. It passes through two points P and Q separated by a distance with velocity `30km//h` and `40 km//h` respectively. The velocity of the car midway between P and Q is
View Solution
Exercise questions and complete solutions for chapter MOTION IN ONE DIMENSION of NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE) of Class 12