Complete Solutions to Exercise of chapter ROTATIONAL MOTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ROTATIONAL MOTION |
| NEET PREVIOUS YEAR | Exercise |
| Number Of Questions | 74 |
| Academic Year | 2023-24 |
Two discs of same moment of inertia rotating their regular axis passing through centre and perpendicular to the plane of disc with angular velocities `omega_(1)` and `omega_(2)`. They are brought into contact face to the face coinciding the axis of rotation. The expression for loss of enregy during this process is :
View SolutionFrom a disc of radius `R` and mass `M`, a circular hole of diameter `R`, whose rim passes through the centre is cut. What is the moment of inertia of remaining part of the disc about a perependicular axis, passing through the centre ?
View SolutionA disc and a solid sphere of same radius but different masses roll off on two inclined planes of the same altitude and length. Which one of the two objects gets to the bottom of the plane first ?
View SolutionTwo rotating bodies `A` and `B` of masses `m` and `2m` with moments of inertia `I_(A)` and `I_(B) (I_(B) gt I_(A))` have equal kinetic energy of rotation. If `L_(A)` and `L_(B)` be their angular momenta respectively, then
View SolutionA solid sphere of mass `m` and radius `R` is rotating about its diameter. A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic emergies of rotation `(E_("sphere")//E_("cylinder"))` will be.
View SolutionA light rod of length `l` has two masses `m_1` and `m_2` attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
View SolutionThree idential spherical shells each of mass `m` and radius `r` are placed as shown in Fig. Consider an axis XX' which is touching the two shells and passing through diameter of third shell. Moment of Inertia of the system consisting of these three spherical shells about XX' as axis is :
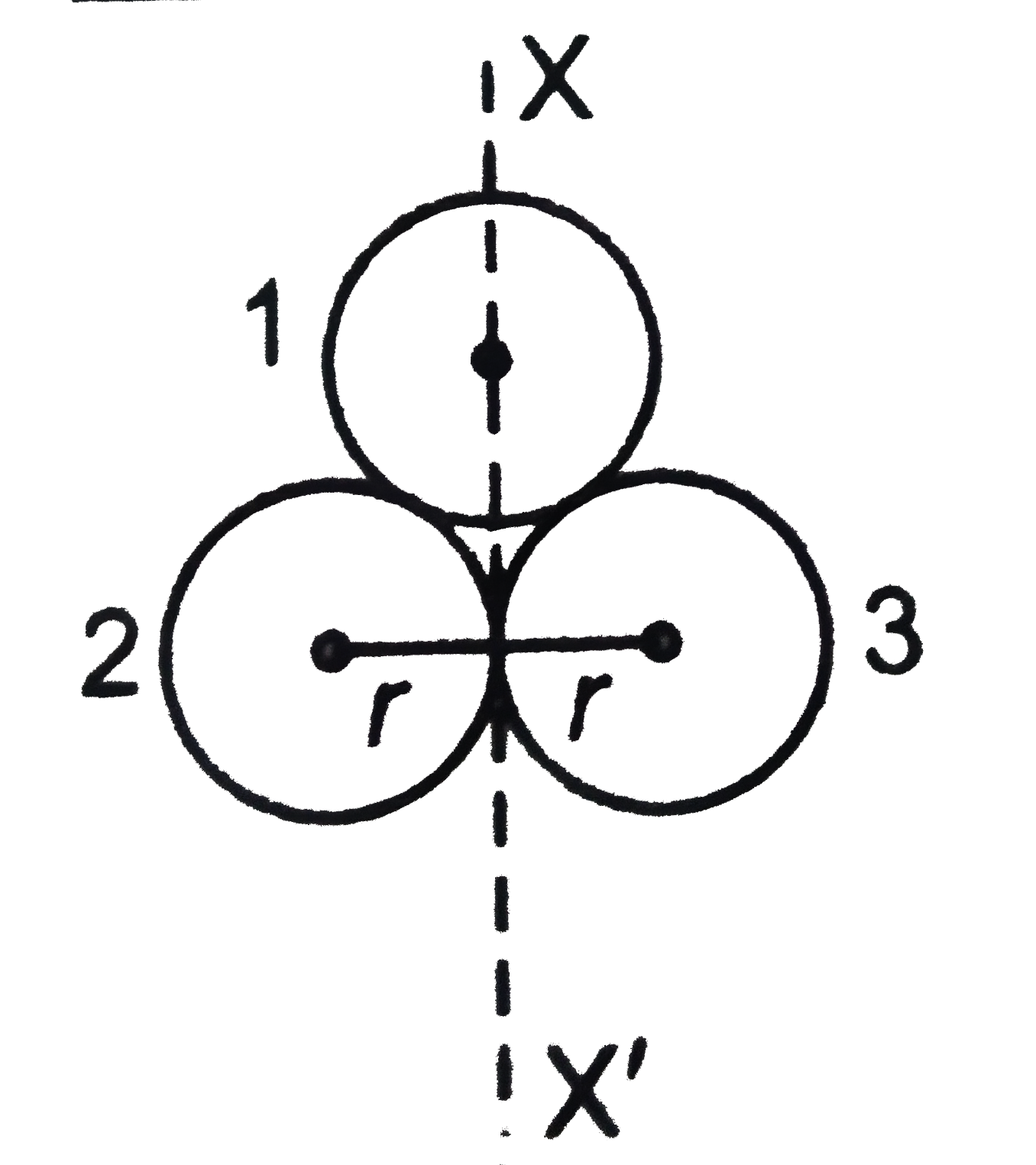
View SolutionPoint masses `m_(1) and m_(2)` are placed at the opposite ends of a rigid rod of length `L`, and negligible mass. The rod is to be set rotating about an axis perpendicualr to it. The position of point `P` on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity `omega_(0)` is minimum, is given by :
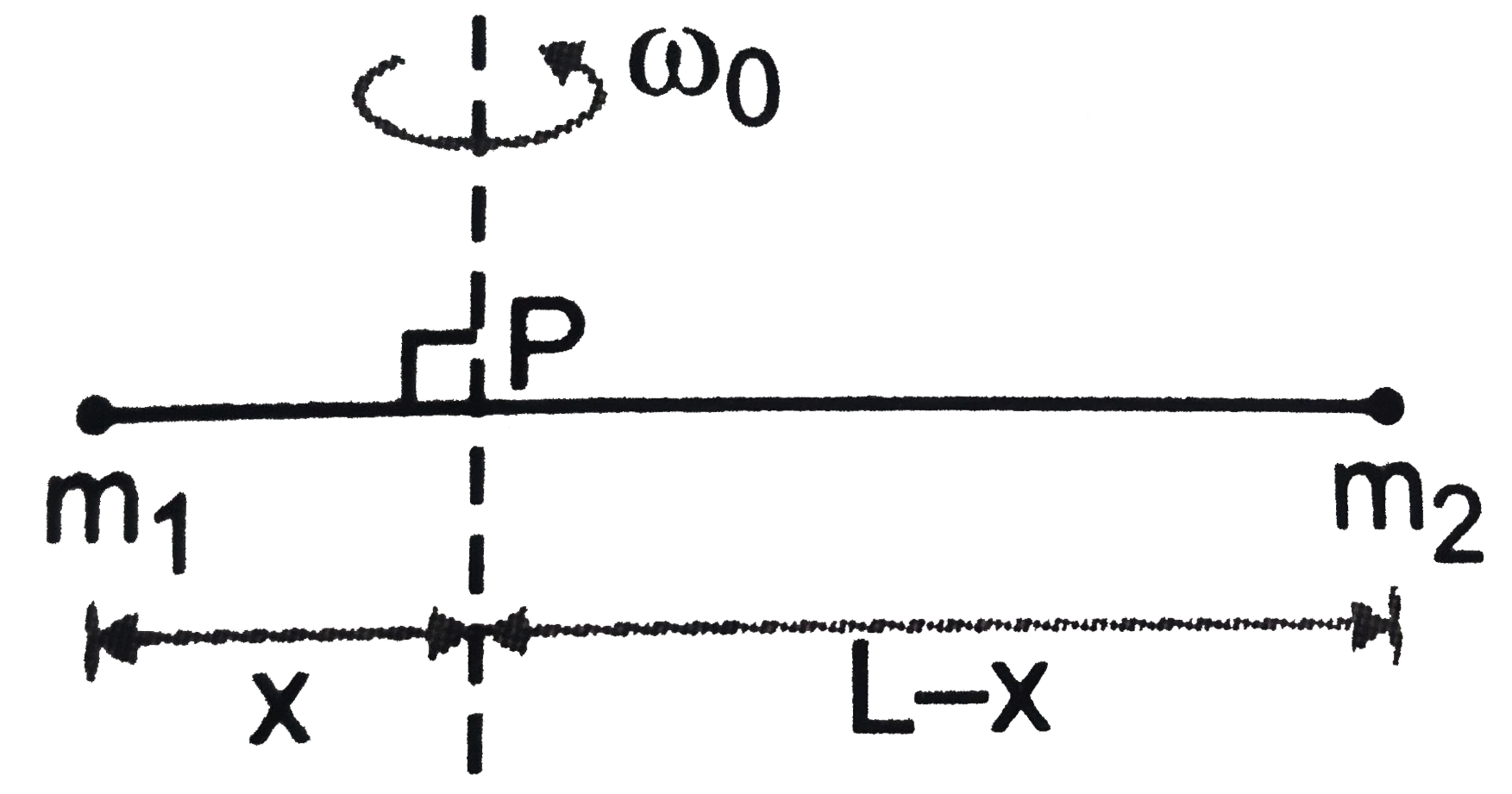
View SolutionAn autmobile moves on road with a speed of `54 km//h`. The radius of its wheel is `0.45 m` and the moment of inertia of the wheel about its axis of rotation is `3 kg m^(2)`. If the vehicle is brought to rest in `15 s`, the magnitude of average torque tansmitted by its brakes to the wheel is :
View SolutionA solid cylinder of mass `50 kg` and radius `0.5 m` is free to rotate about the horizontal axis. A massless string is wound round the cylinder with one end attached to it and other end hanging freely. Tension in the string required to produce an angular acceleration of `2` revolution `s^(-2)` is
View SolutionThe ratio of the accelerations for a solid sphere (mass `m, and radius R`) rolling down an incline of angle `theta` without slipping, and slipping down the incline without rolling is
View SolutionA rod `PQ` of mass `M` and length `L` is hinged at end `P`. The rod is kept horizontal by a massless string tied to point `Q` as shown in the figure. When string is cut, the initial angular accleration of the rod is.

View SolutionA small object of uniform density rolls up a curved surface with an initial velocity v. it reaches up to a maximum height of `(3v^2)/(4g)`
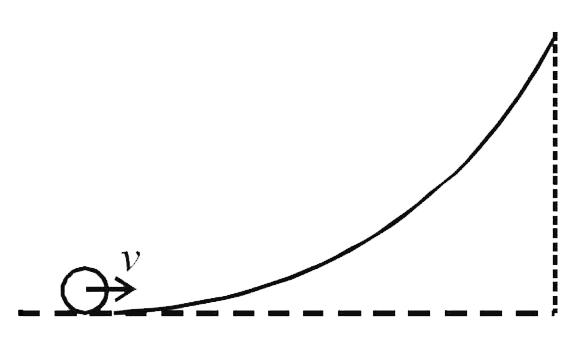
with respect to the initial position. The object is
View SolutionWhen a mass is rotating in a plane about a fixed point, its angular momentum is directed along.
View SolutionTwo persons of masses `55 kg` and `65 kg` respectively are at the opposite ends of a boat. The length of the boat is `3.0 m` and weights `100 kg`. The `55 kg` man walks up to the `65 kg` man and sits with him. If the boat is in still water the centre of mass of the system shifts by.
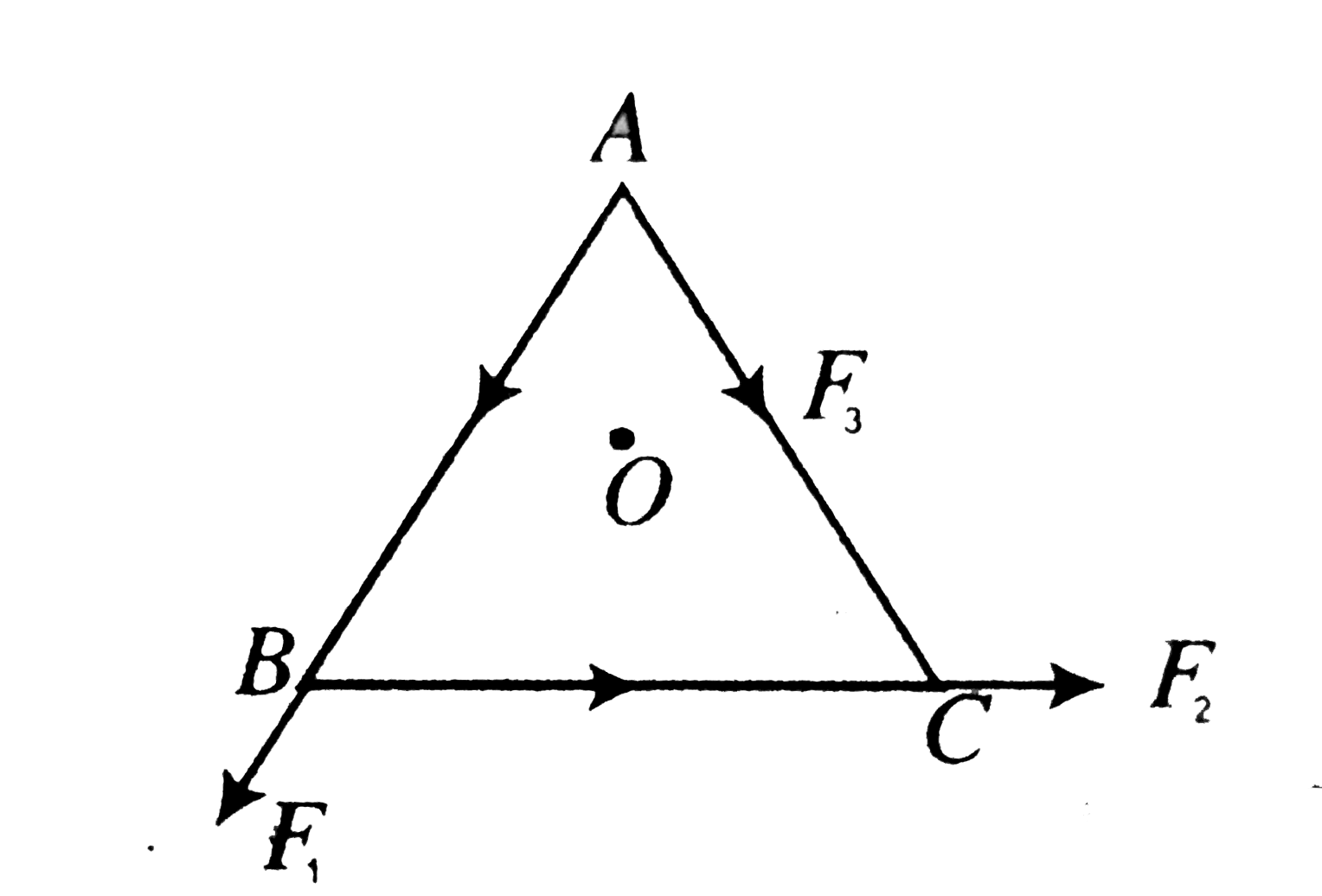
View Solution`O` is the centre of an equilateral triangle `ABC`. `F_(1), F_(2)` and `F_(3)` are the three forces acting along the sides `AB, BC` and `AC` respectively. What should be the value of `F_(3)` so that the total torque about `O` is zero?
View SolutionA particle moves in a circle of radius 5 cm with constant speed and time period `0.2pis`. The acceleration of the particle is
View SolutionThe instantaneous angular position of a point on a rotating wheel is given by the equation
`theta(t) = 2t^(3) - 6 t^(2)`
The torque on the wheel becomes zero at
View SolutionThe moment of inertia of a thin uniform rod of mass `M` and length `L` about an axis passing through its mid-point and perpendicular to its length is`I_0`. Its moment of inertia about an axis passing through one of its ends perpendicular to its length is.
View SolutionA circular disc of moment of inertia `I_(t)` is rotating in a horizontal plane about its symmetry axis with a constant angular velocity `omega_(i)`. Another disc of moment of inertia `I_(b)` is dropped co-axially onto the rotating disc. Initially, the second disc has zero angular speed. Eventually, both the discs rotate with a constant angular speed `omega_(f)`. Calculate the energy lost by the initially rotating disc due to friction.
View SolutionTwo particle which are initially at rest move towards each other under the action of their internal attraction. If their speeds are `v` and `2 v` at any instant, then the speed of centre of mass of the system will be
View SolutionA gramphone record is revolving with an angular velocity `omega`. A coin is placed at a distance `R` from the centre of the record. The static coefficient of friction is `mu`. The coin will revolve with the record if
View SolutionFour identical thin rods each of mass `M` and length `l`, from a square frame. Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is
View SolutionTwo bodies of mass `1 kg` and `3 kg` have position vectors `hat i+ 2 hat j + hat k` and `- 3 hat i- 2 hat j+ hat k`, respectively. The centre of mass of this system has a position vector.
View SolutionA thin circular ring of mass `M` and radius `R` is rotating in a horizontal plane about an axis vertical to its plane with a constant angular velocity `omega`. If two objects each of mass `m` be attached gently to the opposite ends of a diameter of the ring, the ring will then rotate with an angular velocity
View SolutionIf `vec F` is the force acting in a particle having position vector `vec r` and `vec tau` be the torque of this force about the origin, then
View SolutionA thin rod of length `L` and mass `M` is bent at its midpoint into two halves so that the angle between them is `90^@`. The moment of inertia of the bent rod about an axis passing through the bending point and perpendicular to the plane defined by the two halves of the rod is.
View SolutionThe ratio of the radii of gyration of a circular disc to that of a circular ring, each of same mass and radius, around their respective axes is.
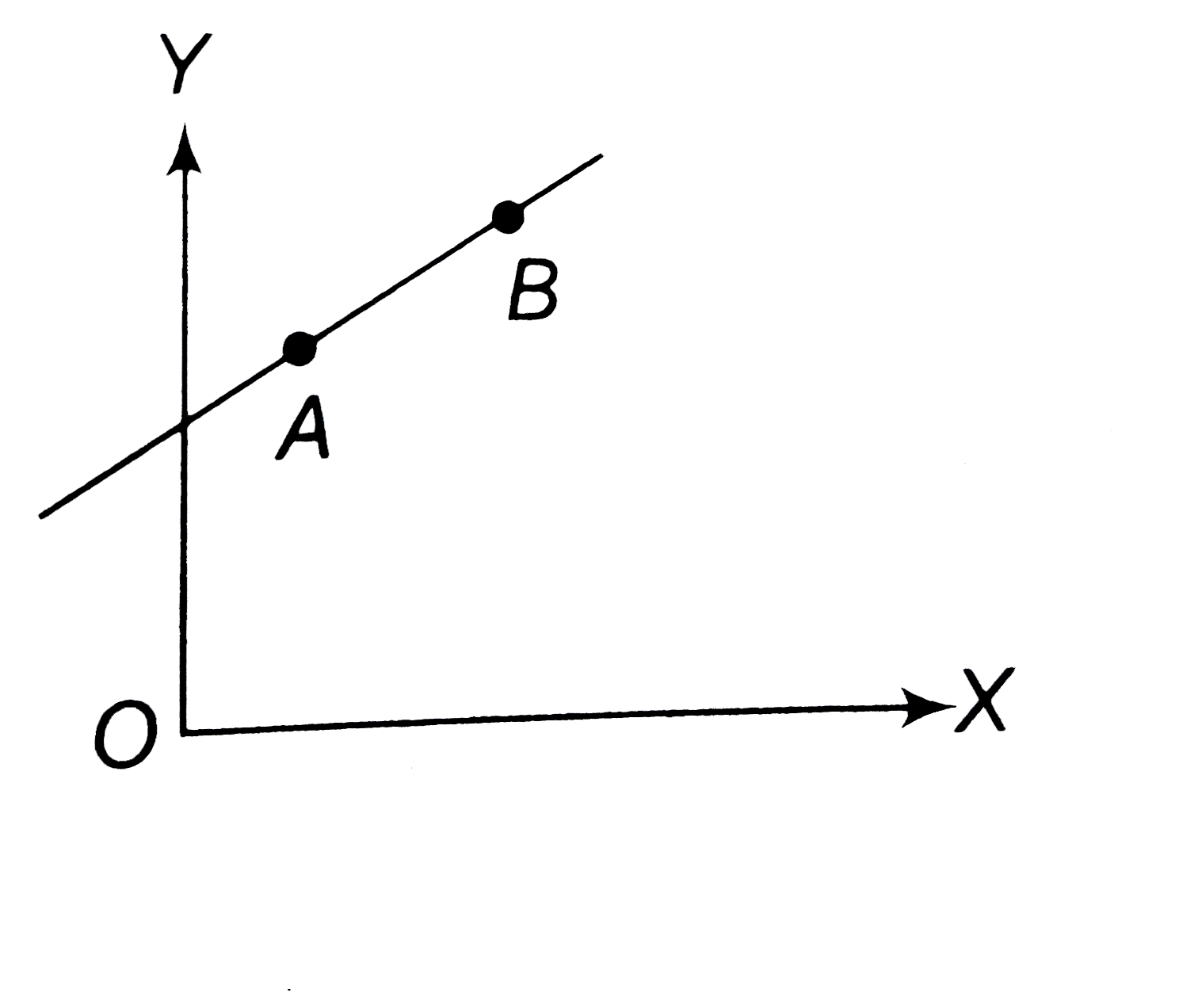
View SolutionA particle of mass `m` moves in the `XY` plane with a velocity `v` along the straight line `AB`. If the angular momentum of the particle with respect to origin `O` is `L_(A)` when it is at A and `L_(B)` when it is at B, then
View SolutionA wheel has angular acceleration of `3.0 rad//s^2` and an initial angular speed of `2.00 rad//s`. In a tine of `2 s` it has rotated through an angle (in radian) of
View SolutionA uniform rod of length `l` and mass `m` is free to rotate in a vertical plane about `A` as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

View SolutionA tube of length L is filled completely with an incomeressible liquid of mass M and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity `omega.` The force exerted by the liquid at the other end is
View SolutionThe moment of inertia of a uniform circular disc of radius `R` and mass `M` about an axis passing from the edge of the disc and normal to the disc is.
View SolutionTwo bodies have their moments of inertia `I` and `2 I` respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular momenta will be in the ratio.
View SolutionThree particles, each of mass `m` grams situated at the vertices of an equilateral triangle `AbC` of side `I` cm (as shown in the figure). The moment of inertia of the system about a line `AX` perpendicular to `AB` and in the plane of `ABC`, in gram-cm^2 units will be.
 .
.
View SolutionConsider a system of two particles having masses `m_(1)` and `m_(2)`. If the particle of mass `m_(1)` is pushed towards the centre of mass of particles through a distance `d`, by what distance would the particle of mass `m_(2)` move so as to keep the mass centre of particles at the original position?
View SolutionA round disc of moment of inertia `I_2` about its axis perpendicular to its plane and passing through its centre is placed over another disc of moment of inertia `I_1` rotating with an angular velocity `omega` about the same axis. The final angular velocity of the combination of discs is.
View SolutionThe ratio of the radii of gyration of a circular disc about a tangential axis in the plane of the disc and a circular ring of the same radius about a tengential axis in the plane of the ring is
View SolutionA ball rolls without slipping. The radius of gyration of the ball about an axis passing through its centre of mass is `k`. If radius of the ball be `R`, then the fraction of total energy associated with its rotation will be.
View SolutionA thin circular ring of mass M and radius R is rotating about its axis with a constant angular velocity omega. Four objects each of mass m, are kept gently to the opposite ends of two perpendicular diameters of the ring. The angular velocity of the ring will be
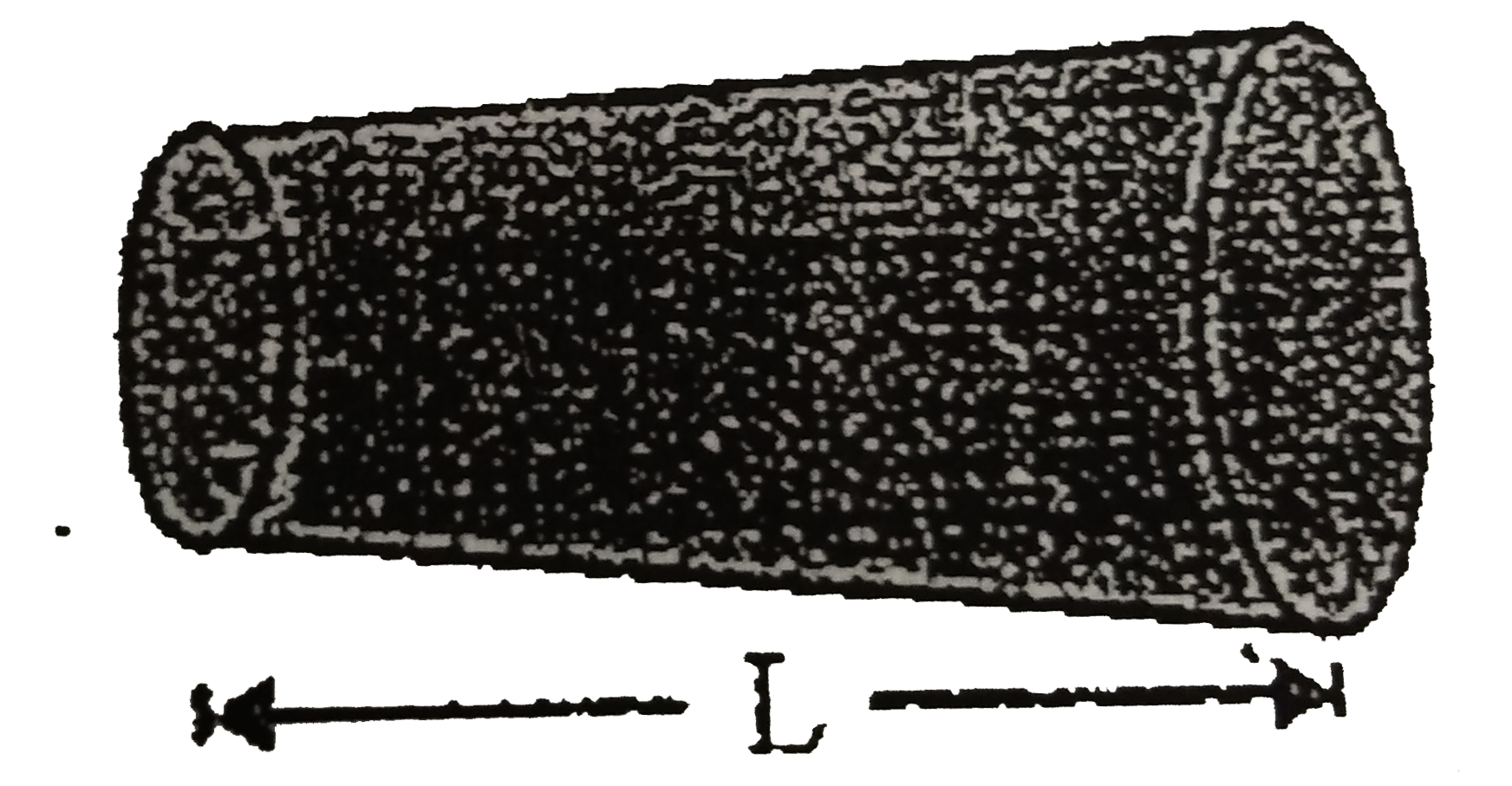
View SolutionA rod of length L is of non uniform cross-section. Its mass per unit length varies linearly with distance from left end. Then its centre of mass from left end is at a distance. (Take linear density at left end=0).
View SolutionA solid sphere of radius `R` is placed on a smooth horizontal surface. A horizontal force `F` is applied at height `h` from the lowest point. For the maximum acceleration of the centre of mass
View SolutionA circular disc is to be made by using iron and aluminium, so that it acquires maximum moment of inertia about its geometrical axis. It is possible with
View SolutionA disc is rotating with angular velocity `omega`. If a child sits on it, what is conserved?
View SolutionA wheel of bicycle is rolling without slipping on a level road. The velocity of the centre of mass is `v_(CM)`, then true statement is

View SolutionA particle of mass `M` is revolving along a circule of radius `R` and nother particle of mass `m` is recolving in a circle of radius `r`. If time periods of both particles are same, then the ratio of their angular velocities is
View SolutionABC is a right angled triangular plate of uniform thickness. The sides are such that `AB gt BC` as shown in figure. `I_(1), I_(2), I_(3)` are moments of inertia about `AB, BC` and `AC` respectively. Then which of the following relations is correct?

View SolutionThree identical metal balls each of radius `r` are placed touching each other on a horizontal surface such that an equilateral triangle is formed, when the center of three balls are joined. The center of mass of system is located at the
View SolutionThe moment of inertia of a disc of mass `M` and radius `R` about a tangent to its rim in its plane is
View Solution`O` is the centre of an equilateral triangle `ABC`. `F_(1), F_(2)` and `F_(3)` are the three forces acting along the sides `AB, BC` and `AC` respectively. What should be the value of `F_(3)` so that the total torque about `O` is zero?

View SolutionA ball of mass `0.25kg` attached to the end of a string of length `1.96m` moving in a horizontal circle. The string will break if the tension is more than `25N`. What is the maximum speed with which the ball can be moved.
View SolutionA couple produces.
View SolutionA cart of mass `M` is tied to one end of a massless rope of length `10 m`. The other end of the rope is in the hands of a man of mass `M`. The entire system is on a smooth horizontal surface. The man is at `x=0` and the cart at `x=10 m`. If the man pulls the cart by the rope, the man and the cart will meet at the point
View SolutionIn a carbon monoxide molecule, the carbon and the oxygen atoms are separated by a distance `1.2xx10^-10m`. The distance of the centre of mass from the carbon atom is
View SolutionIf a flywheel makes `120" rev"//"min"`, then its angular speed will be
View SolutionThe angular momentum of a body with mass (m) moment of inertia `(I)` and angular velocity `(omega)" rad"//s` is equal to
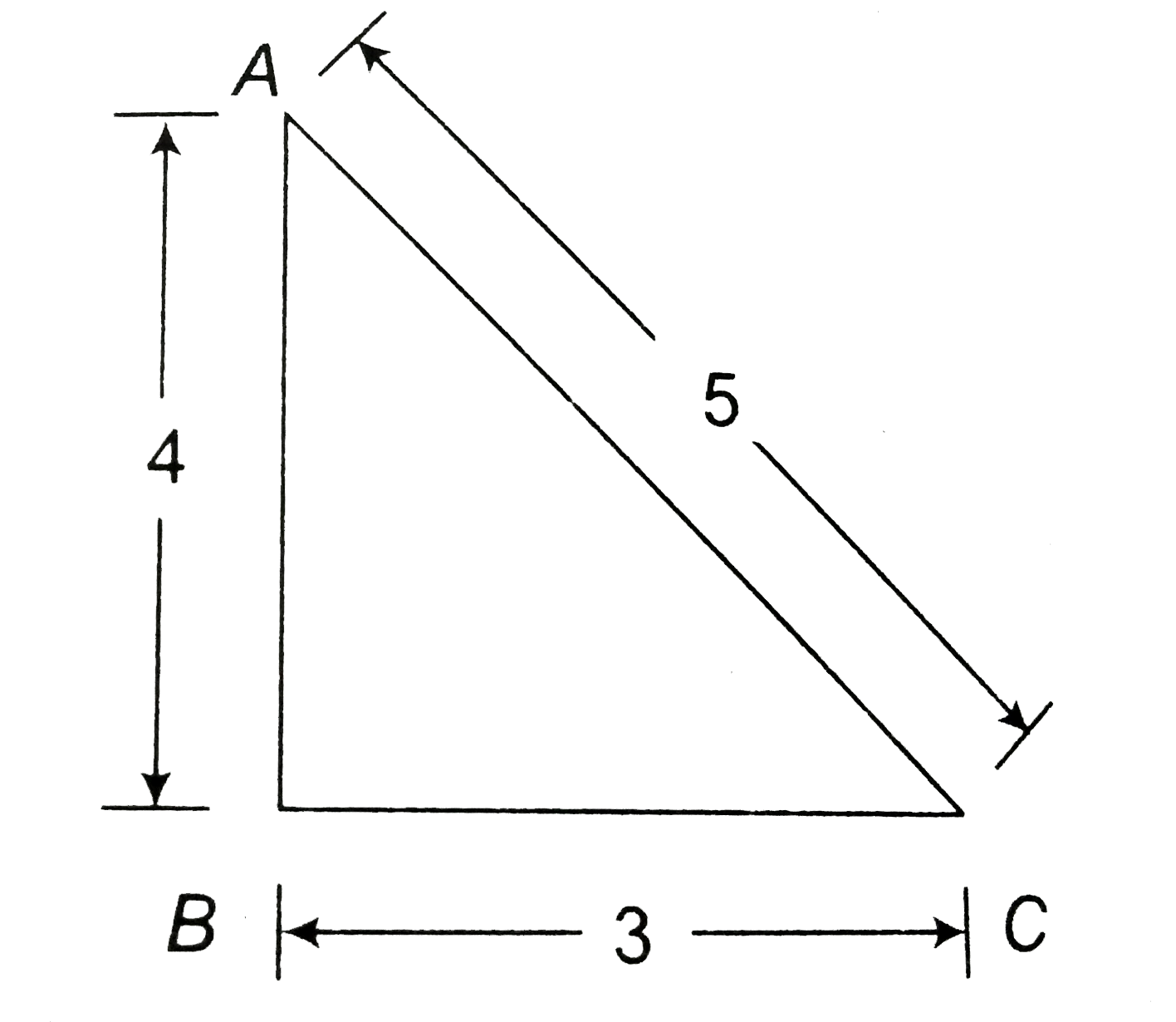
View Solution`ABC` is a traiangular plate of uniform thickness. The sides are in the ratio shown in the figure. `I_(AB)`, `I_(BC)` and `I_(CA)` are the moments of inertia of the plate about `AB`, `BC` and `CA` repectively. Which one of the following relations is correct?
View SolutionThe angular speed of an engine wheel making `90" rev"//"min"` is
View SolutionTwo racing cars of masses `m` and `4m` are moving in circles of radii `r` and `2r` respectively. If their speeds are such that each makes a complete circle in the same time, then the ratio of the angular speeds of the first to the second car is
View SolutionIf a spherical ball rolls on a table without slipping, the fraction of its total energy associated with rotation is
View SolutionA thin uniform circular ring is rolling down an inclined plane of inclination `30^(@)` without slipping. Its linear acceleration along the inclined plane will be
View SolutionAngular momentum is
View SolutionIn a rectangle `ABCD (BC=2AB)`. The moment of inertia is minimum along axis through

View SolutionA solid sphere, disc and solid cylinder, all of the same mass, are allowed to roll down (from rest) on inclined plane, them
View SolutionThe speed of a homogeneous solid sphere after rolling down an inclined plane of vertical height `h` from rest without slipping will be.
View SolutionA particle of mass `m=5 kg` is moving with a uniform speed `v=3 sqrt(2)` in the `XOY` plane along the line `Y=X+4`. The magnitude of the angular momentum of the particle about the origin is
View SolutionIf a sphere is rolling, the ratio of the translation energy to total kinetic energy is given by
View SolutionThe moment of inertia of a body about a given axis is `1.2 kg m^(2)`. Initially, the body is at rest. In order to produce a rotational `KE` of `1500 J`, for how much duration, an acceleration of `25 rad s^(-2)` must be applied about that axis ?
View SolutionMoment of inertia of a uniform circular disc about a diameter is `I`. Its moment of inertia about an axis perpendicular to its plane and passing through a point on its rim will be.
View SolutionA fly wheel rotating about a fixed axis has a kinetic energy of `360 J`. When its angular speed is `30 rad s^(-1)`. The moment of inertia of the wheel about the axis of rotation is
View SolutionAt any instant, a rolling body may be considered to be in pure rotation about an axis through the point of contact. This axis is translating forward with speed
View SolutionA solid cylinder of mass `M` and radius `R` rolls down an inclined plane of height `h` without slipping. The speed of its centre when it reaches the bottom is.
View SolutionA ring of mass `m` and radius `r` rotates about an axis passing through its centre and perpendicular to its plane with angular velocity `omega`. Its kinetic energy is
View SolutionA solid homogeneous sphere is moving on a rough horizontal surface, partly rolling and partly sliding. During the king of motion of the sphere.
View Solution
Exercise questions and complete solutions for chapter ROTATIONAL MOTION of NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE) of Class 12