Complete Solutions to Gravitation of chapter GRAVITATION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | GRAVITATION |
| NEET PREVIOUS YEAR | Gravitation |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
The acceleration due to gravity at a height `1km` above the earth is the same as at a depth `d` below the surface of earth. Then :
View SolutionTwo astronauts are floating in gravitational free space after having lost contanct with their spaceship. The two will:
View SolutionAt what height from the surface of earth the gravitation potential and the value of `g` are `- 5.4 xx 10^(7) J kg^(-2)` and `6.0 ms^(-2)` respectively ? Take the radius of earth as `6400 km`:
View SolutionThe ratio of escape velocity at earth `(v_(e))` to the escape velocity at a planet `(v_(y))` whose radius and density are twice
View SolutionThe dependence of acceleration due to gravity `g` on the distance `r` from the centre of the earth, assumed to be a sphere of radius `R` of uniform density is as shown in Fig. below:

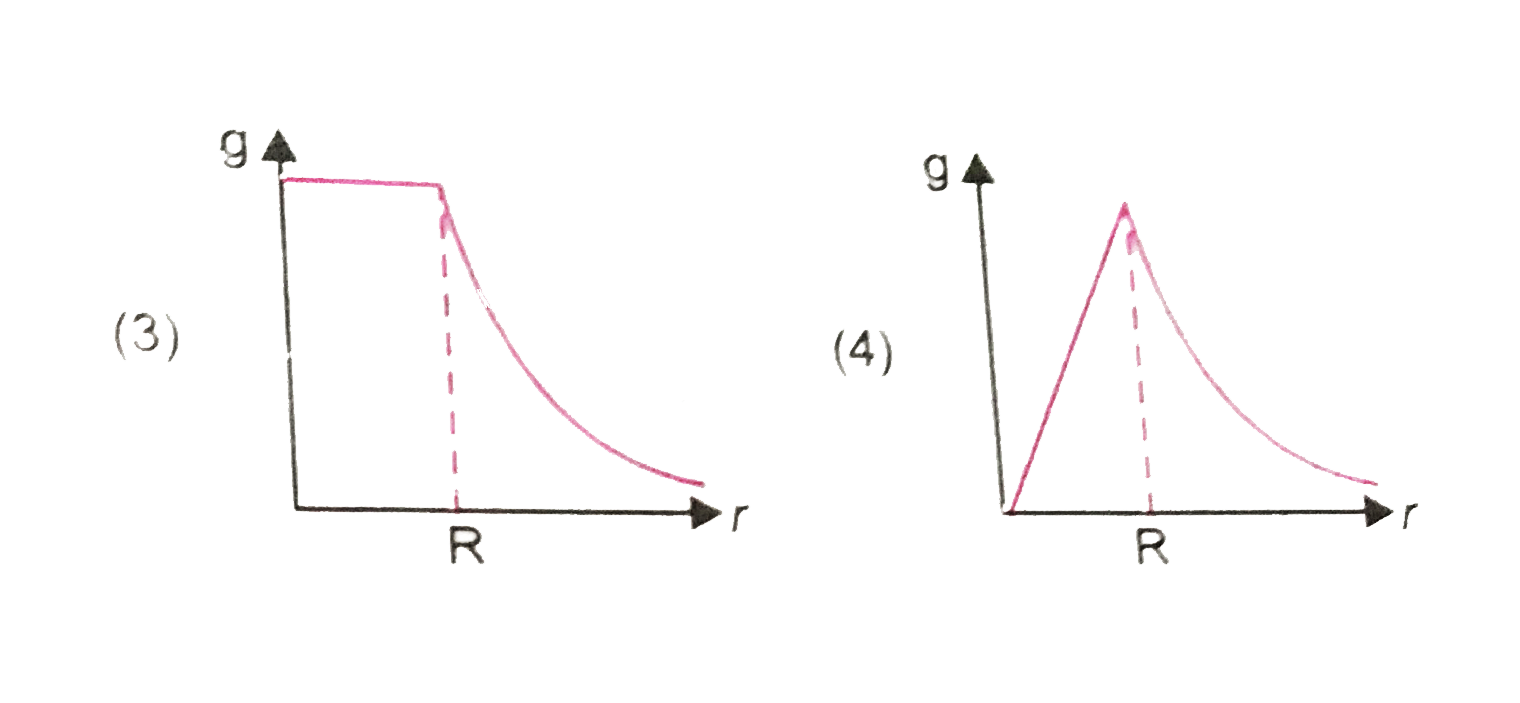
The correct figure is
View SolutionA satellite of mass `m` is orbiting the earth (of radius `R`) at a height `h` from its surface. The total energy of the satellite in terms of `g_(0)`, the value of acceleration due to gravity at the earth's surface,
View SolutionKepler's third law states that square of period revolution `(T)` of a planet around the sun is proportional to third power of average distance `i` between sun and planet i.e. `T^(2)=Kr^(3)`
here `K` is constant
if the mass of sun and planet are `M` and `m` respectively then as per Newton's law of gravitational the force of alteaction between them is `F=(GMm)/(r^(2))`, here `G` is gravitational constant. The relation between `G` and `K` is described as
View SolutionTwo spherical bodies of mass M and 5M & radii R & 2R respectively are released in free space with initial separation between their centres equal to 12R. If they attract each other due to gravitational force only, then the distance covered by the smallar body just before collision is
View SolutionA remote-sensing satellite of earth revolves in a circular orbit at a hight of `0.25xx10^(6)m` above the surface of earth. If earth's radius is `6.38xx10^(6)m` and `g=9.8ms^(-2)`, then the orbital speed of the satellite is
View SolutionA satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
View SolutionA black hole is an object whose gravitational field is so strong that even light cannot escape from it. To what approximate radius would earth (mass `=5.98xx10^(24)kg`) have to be compresed to be a black hole?
View SolutionDependence of intensity of gravitational field `(E)` of earth with distance `(r)` from centre of earth is correctly represented by
View SolutionInfinite number of bodies, each of mass `2kg`, are situated on `x`-axis at distance `1m,2m,4m,8m.........` respectively, from the origin. The resulting gravitational potential the to this system at the origing will be
View SolutionThe height a which the weight of a body becomes `1//16th` its weight on the surface of earth (radius `R`) is
View SolutionA compose needle which is allowed to move in a horizontal plane is taken to a geomagnetic pole. It
View SolutionA spherical planet far out in space has a mass `M_(0)` and diameter `D_(0)`. A particle of mass m falling freely near the surface of this planet will experience an accelertion due to gravity which is equal to
View SolutionA geostationary satellite is orbiting the earth at a height of `5R` above the surface of the earth, `2R` being the radius of the earth. The time period of another satellite in hours at a height of `2R` form the surface of the earth is
View SolutionA plenet moving along an elliptical orbit is closest to the sun at a distance `r_(1)` and farthest away at a distance of `r_(2)`. If `v_(1)` and `v_(2)` are the linear velocities at these points respectively, then the ratio `(v_(1))/(v_(2))` is
View SolutionA body projected vertically from the earth reaches a height equal to earth's radius before returning to the earth. The power exerted by the gravitational force is greatest.
View SolutionThe radii of circular orbits of two satellite `A` and `B` of the earth are `4R` and `R`, respectively. If the speed of satellite `A` is `3v`, then the speed of satellite `B` will be
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance `a/2` from the centre.
View Solution_S01_025_Q01.png)
The figure shows elliptical orbit of a planet m about the sun S. the shaded area SCD is twice the shaded area SAB. If `t_(1)` be the time for the planet to move from C to D and `t_(2)` is the time to move from A to B, then:
View SolutionA roller coaster is designed such that riders experience "weightlessness" as they go round the top of a hill whose radius of curvature is `20m`. The speed of the car at the top of the hill is between
View SolutionTwo satellites of earth `S_(1)` and `S_(2)` are moving in the same orbit. The mass of `S_(1)` is four times the mass of `S_(2)`. Which one of the following statements is true?
View SolutionThe earth is assumed to be a sphere of raduis `R`. A plateform is arranged at a height `R` from the surface of the `fv_(e)`, where `v_(e)` is its escape velocity form the surface of the earth. The value of `f` is
View SolutionFor a satellite moving in an orbit around the earth, ratio of kinetic energy to potential energy is
View SolutionImagine a new planet having the same density as that of earth but `3` times bigger than the earth in size. If the acceleration due to gravity on the surface of earth is `g` and that on the new plane is `g` , then :
View SolutionThe density of a newly discovered planet is twice that of earth. The acceleration due to gravity at the surface of the planet is equal to that at the surface of the earth. If the radius of the earth is `R`, the radius of the planet would be
View SolutionTwo sphere of masses `m` and `M` are situated in air and the gravitational force between them is `F`. The space around the masses in now filled with a liquid of specific gravity `3`. The gravitational force will now be
View SolutionThe acceleration due to gravity on the planet `A` is `9` times the acceleration due to gravity on planet `B`. A man jumps to a height of `2m` on the surface of `A`. What is the height of jump by the same person on the planet `B`?
View SolutionA body of mass `m` is placed on the earth surface is taken to a height of `h=3R`, then, change in gravitational potential energy is
View SolutionA body attains a height equal to the radius of the earth when projected from earth's surface the velocity of body with which it was projected is
View SolutionThe mass of a planet is six times that of the earth. The radius of the planet is twice that of the earth. It's the escape velocity from the earth is `v`, then the escape velocity from the planet is:
View SolutionThe escape velocity of a sphere of mass m is given by (G= univesal gravitational constant, `M_(e) =` mass of the earth and `R_(e) =` radius of the earth)
View SolutionA rubber ball is dropped from a height of `5m `on a plane, where the acceleration due to gravity is not shown. On bouncing it rises to `1.8 m.` The ball loses its velocity on bouncing by a factor of
View SolutionThe time of revolution of planet `A` round the sun is `8` times that of another planet `B`. The distance of planet `A` from the sun is how many `B` from the sun
View SolutionEscape velocity of a body from the surface of earth is 11.2km/sec. from the earth surface. If the mass of earth becomes double of its present mass and radius becomes half of its present radius then escape velocity will become
View SolutionA ball is dropped from a spacecraft revolving around the earth at a height of `1200km`. What will happen to the ball ? .
View SolutionWhat will be the formula of the mass in terms of `g`, `R` and `G` ? (`R` = radius of the earth)
View SolutionThe escape velocity from the surface of the earth is `V_(e)`. The escape velcotiy from the surface of a planet whose mass and radius are three times those of the earth, will be
View SolutionA satellite A of mass m is at a distance of r from the centre of the earth. Another satellite B of mass 2m is at distance of 2r from the earth's centre. Their time periode are in the ratio of
View SolutionThe escape velocity for a body projected vertically upwards from the surface of the earth is `11.2 km s^(-1)`. If the body is projected in a direction making an angle `45^@` with the vertical, the escape velocity will be
View SolutionThe mean radius of earth is R, its angular speed on its own axis is w and the acceleration due to gravity at earth's surface is g. What will be the radius of the orbit of a geostationary satellite
View SolutionA satellite moves around the earth in a circular orbit with speed `v`. If `m` is the mass of the satellite, its total energy is
View SolutionA seconds pendulum is mounted in a rocket. Its period of oscillation decreases when the rocket
View SolutionA planet is moving in an elliptic orbit. If `T,V,E` and `L` stand, respectively, for its kinetic energy, gravitational potential energy, total energy and angular momentum about the centre of force, then
View SolutionThe gravitational force between two objects is proportional to `1//R` (and not as `1//R^(2)`) where `R` is separation between them, then a particle in circular orbit under such a force would have its orbital speed `v` proportional to
View SolutionFor a satellite, escape speed is `11 km s^(-1)`. If the satellite is launched at an angle of `60^(@)` with the vertical, what will be the escape speed?
View SolutionThe distance of the two planets from the Sun are `10^(13)m` and `10^(12) m`, respectively. Find the ratio of time periods and speeds of the two planets.
View SolutionThe largest and the shortest distance of the earth from the sun are `r_(1)` and `r_(2)`, its distance from the sun when it is at the perpendicular to the major axis of the orbit drawn from the sun
View Solution
Gravitation questions and complete solutions for chapter GRAVITATION of NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE) of Class 12