Complete Solutions to Atomic Physics of chapter ATOMIC PHYSICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ATOMIC PHYSICS |
| NEET PREVIOUS YEAR | Atomic Physics |
| Number Of Questions | 39 |
| Academic Year | 2023-24 |
Radioactive material `A` has decay constant `8 lamda` and material `B` has decay constant `lamda`. Initial they have same number of nuclei. After what time, the ratio of number of nuclei of material `B` to that `A` will be `(1)/( e)` ?
View SolutionThe ratio of wavelength of the lest line of Balmer series and the last line Lyman series is:
View SolutionIf an electron in a hydrogen atom jumps from the `3rd` orbit to the `2nd` orbit, it emits a photon of wavelength `lambda`. When it jumps form the `4th` orbit to the `3dr` orbit, the corresponding wavelength of the photon will be
View SolutionA proton and an alpha particle both enters a region of uniform magnetic field `B`, moving at right angles to the field `B`. If the radius of circular orbits for both the particles is equal and the kinetic energy acquired by proton is `1 MeV`, the energy acquired by the alpha particles will be :
View SolutionIn the spectrum of hydrogen atom, the ratio of the longest wavelength in Lyman series to the longest wavelangth in the Balmer series is:
View SolutionConsider `3rd` orbit of `He^(+)` (Helium) using nonrelativistic approach the speed of electron in this orbit will be (given `K = 9 xx 10^(9)` constant `Z = 2` and `h` (Planck's constant) `= 6.6 xx 10^(-34)Js`.)
View SolutionHydrogen atom in ground state is excited by a monochromatic radiation of `lambda = 975 Å`. Number of spectral lines in the resulting spectrum emitted will be
View SolutionIn the spectrum of hydrogen atom, the ratio of the longest wavelength in Lyman series to the longest wavelangth in the Balmer series is:
View SolutionElectron in hydrogen atom first jumps from third excited state to second excited state and then form second excited state to first excited state. The ratio of wavelength `lambda_(1): lambda_(2)` emitted in two cases is
View SolutionAn electrons of a stationary hydrogen aton passes form the fifth enegry level to the ground level. The velocity that the atom acquired as a result of photon emission will be
`(m` is the mass of the electron, `R`, Rydberg constanrt and `h`, Planck's constant)
View SolutionThe wavelength of the first line of Lyman series for hydrogen atom is equal to that of the second line of Balmer series for a hydrogen-like ion. The atomic number `Z` of hydrogen-like ion is
View SolutionThe energy of a hydrogen atom in the ground state is `-13.6 eV`. The eneergy of a `He^(+)` ion in the first excited state will be
View SolutionThe ionization enegry of the electron in the hydrogen atom in its ground state is `13.6 eV`. The atoms are excited to higher energy levels to emit radiations of `6` wavelengths. Maximum wavelength of emitted radiation corresponds to the transition between
View SolutionIn a Rutherford scattering experiment when a projectile of change `Z_(1)` and mass `M_(1)` approaches s target nucleus of change `Z_(2)` and mass `M_(2)`, te distance of closed approach is `r_(0)`. The energy of the projectile is
View SolutionThe groud state energy of hydrogen atom is `-13.6 eV`. When its electron is in first excited state, its exciation energy is
View SolutionThe total energy of eletcron in the ground state of hydrogen atom is `-13.6 eV`. The kinetic enegry of an electron in the first excited state is
View SolutionIonization potential of hydrogen atom is `13.6 V`. Hydrogen atoms in the ground state are excited by monochromatic radiation of photon energy `12.1 eV`. The spectral lines emitted by hydrogen atoms according to Bohr's theory will be
View SolutionThe total energy of the electron in the first excited state of hydrogen is `-3.4 eV`. What is the kinetic energy of the electron in this state?
View SolutionEnergy `E` of a hydrogen atom with principle quantum number `n` is given by `E = (-13.6)/(n^(2)) eV`. The energy of a photon ejected when the electron jumps from `n = 3` state to `n = 2` state of hydrogen is approximately
View SolutionThe Bohr model of atoms
View SolutionWhich of the following transitions in a hydrogen atom emits photon of the highest frequency ?
View SolutionWhen electron jumps from n = 4 to n = 1 orbit, we get
View SolutionIn the Bohr model of a hydrogen atom, the centripetal force is furnished by the Coulomb attraction between the proton and the electrons. If `a_(0)` is the radius of the ground state orbit, `m` is the mass and `e` is the charge on the electron and `e_(0)` is the vacuum permittivity, the speed of the electron is
View SolutionThe groud state energy of hydrogen atom is `-13.6 eV`. When its electron is in first excited state, its exciation energy is
View SolutionWhen hydrogen atom is in first excited level, its radius is….its ground state radius
View Solutionwhen a hydrogen atom is raised from the ground state to an excited state
View SolutionThe spectrum obtained from a sodium vapour lamp is an example of
View SolutionThe radius of hydrogen atom in its ground state is `5.3 xx 10^(-11)m`. After collision with an electron it is found to have a radius of `21.2 xx 10^(-11)m`. What is the principle quantum number of `n` of the final state of the atom ?
View SolutionIn Rutherford scattering experiment, what will b ethe correct angle for `alpha` scattering for an impact parameter `b = 0` ?
View SolutionHydrogen atoms are excited from ground state of the principle quantum number `4`. Then the number of spectral lines observed will be
View SolutionWhich source is associated with a line emission spectrum?
View SolutionThe ionisation energy of hydrogen atom is `13.6 eV`. Following Bohr's theory, the energy corresponding to a transition between the `3`rd and the `4`th orbit is
View SolutionIn terms of Bohr radius `a_(0)`, the radius of the second Bohr orbit of a hydrogen atom is given by
View SolutionGround state energy of H-atom is -13.6 eV. The energy needed to ionise H-atom from its second excited state is
View SolutionConsider an eelctron in the nth orbit of a hydrogen atom in the Bohr model. The circumference of the orbit can be expressed in terms of the de Broglie wavelength `lambda` o fthat electron as
View SolutionThe valence electron in alkali metal is a
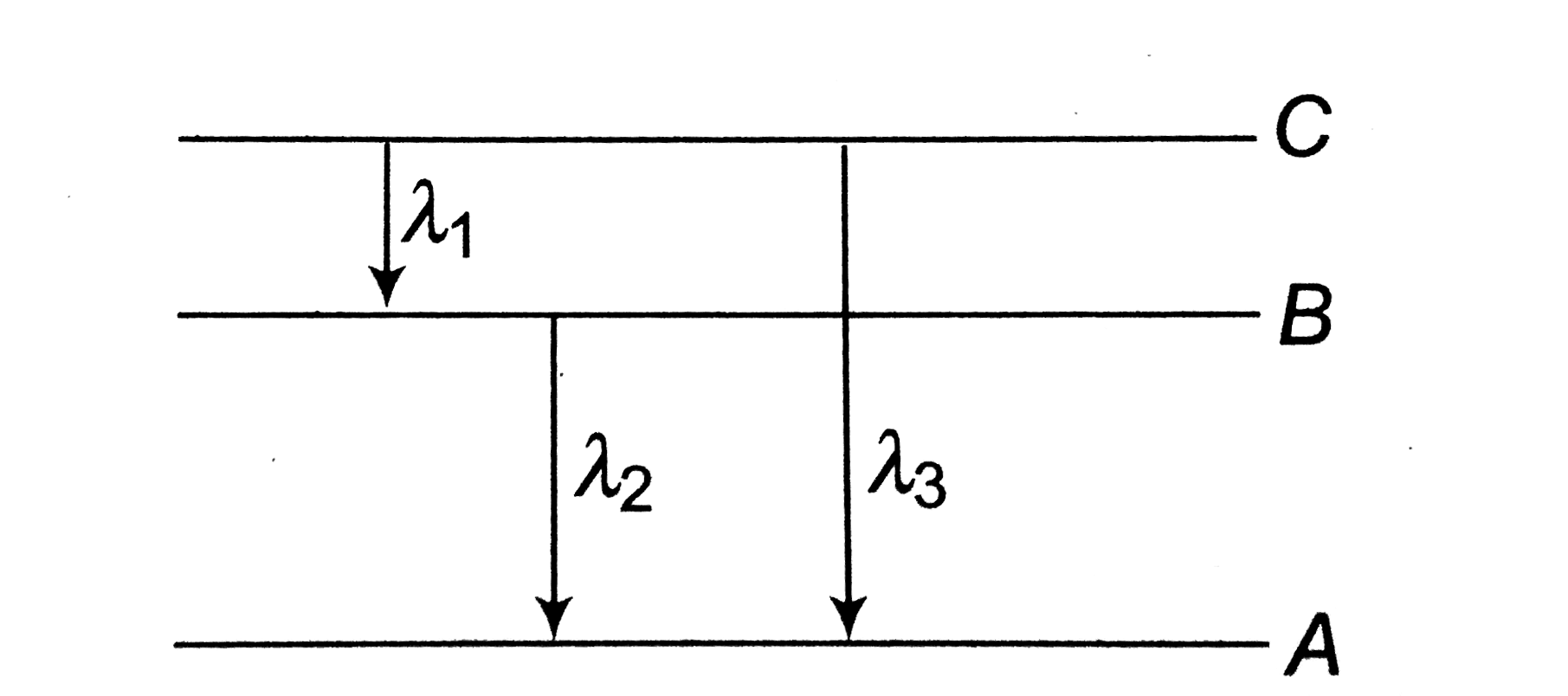
View SolutionEnergy levels `A, B, C` of a certain atom corresponding to increasing values of energy i.e., `E_(A) lt E_(B) lt E_(C)`. If `lambda_(1), lambda_(2), lambda_(3)` are the wavelengths of radiations correspnding to the transitions `C` to `B, B` to `A` and `C` to `A` respectively, which o fthe following statements is correct?
View SolutionTo explain his theory, Bohr used
View SolutionThe ionization energy of hydrogen atom is 13.6 eV. Calculate Rydberg's constant for hydrogen.
View Solution
Atomic Physics questions and complete solutions for chapter ATOMIC PHYSICS of NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE) of Class 12