Complete Solutions to MCQs of chapter कणों के निकाय तथा घूर्णन गति of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | कणों के निकाय तथा घूर्णन गति |
| NEET PREVIOUS YEAR | MCQs |
| Number Of Questions | 70 |
| Academic Year | 2023-24 |
तीन पिण्ड a : ( एक ठोस गोला ), b : ( एक पतली वृत्ताकार चकती ) तथा c : ( एक वृत्ताकार छल्ला ), जिनमें प्रत्येक का द्रव्यमान m तथा त्रिज्या r हैं, समान कोणीय चाल से अपनी सममिति अक्षों के परितः चक्रण कर रहे हैं | इन्हें विरामावस्था में लाने के लिए किए जाने वाले आवश्यक कार्यों ( w ) के लिए कौन - सा सम्बन्ध सही है ?
View Solutionकोई ठोस गोला मुक्त आकाश में अपनी सममिति अक्ष के पारित : मुक्त रूप से घूर्णन कर रहा है | इस गोले का द्रव्यमान समान रखते हुए इसकी त्रिज्या में वृद्धि की जाती है | गोले के लिए निम्नलिखित में से कौन - सी भौतिक राशि स्थिर रहेगी ?
View Solutionएक ठोस गोला लोटनी गति कर रहा है | लोटनी गति में वस्तु की स्थानांतरीय गतिज ऊर्जा `(K_(T))` के साथ - साथ घूर्णी गतिज ऊर्जा `(K_(r))` भी होती है | गोले के लिए `K_(t):(K_(t)+K_(r))` का अनुपात होगा
View Solutionदो डिस्कों ( चक्रिकाओं ) के बल - आघूर्ण आपस में बराबर हैं | ये अपनी - अपनी नियमित अक्ष, जो इनके समतल के लम्बवत हैं और चक्रिका के केंद्र से होकर गुजरती हैं, के परितः `omega_(1)` क्रमश: `omega_(2)` तथा कोणीय वेग से घूर्णन कर रही हैं | इनको एक - दूसरे के सम्मुख इस प्रकार संपर्क में लाया जाता है, कि इनकी घूर्णन अक्ष सम्पाती हो जाती है, तो इस प्रक्रम में ऊर्जा - क्षय के लिए व्यंजक होगा
View Solutionएक खोखले बेलन का द्रव्यमान 3 किग्रा तथा त्रिज्या 40 सेमी है | इस पर एक डोरी लपेट दी गई है | यदि इस डोरी को 30 न्यूटन के बल द्वारा खींचा जाए, तो बेलन का कोणीय त्वरण कितना होगा ?
View Solutionघूर्णन करते हुए दो पिंडों a तथा b के द्रव्यमान क्रमश : m तथा 2m और जड़त्व आघूर्ण क्रमश : `I_(A)` तथा `I_(B)(I_(B) gt I_(A))` इन दोनों की घूर्णन गतिज ऊर्जाएँ आपस में बराबर हैं व इनके कोणीय संवेग क्रमश : `L_(A)` तथा `L_(B)` हो , तो
View Solutionद्रव्यमान m तथा त्रिज्या r का एक ठोस गोला अपने व्यास के पारित : घूर्णन कर रहा है | उसी द्रव्यमान तथा उसी त्रिज्या का एक ठोस बेलन ( सिलेण्डर ) भी अपने ज्यामितीय अक्ष के पारित : घूर्णन कर रहा है | यदि बेलन के घूर्णन की कोणीय चाल गोले से दोगुनी है, तो इन दोनों की घूर्णन गतिज ऊर्जाओं का अनुपात `E_("गोला")//E_("बेलन")` होगा
View Solutionएक हल्की छड़ की लम्बाई l है | इसके दो सिरों से क्रमश : `m_(1)` तथा `m_(2)` द्रव्यमान के पिण्ड संलग्न हैं | इस छड़ के लम्बवत तथा इसके द्रव्यमान केंद्र से गुजरते हुए अक्ष के पारित : इस निकाय का जड़त्व आघूर्ण होगा
View Solutionद्रव्यमान `M` तथा त्रिज्या `R` की किसी डिस्क से `R` व्यास का कोई वृत्ताकार छिद्र इस प्रकार काटा जाता है कि उसकी रिम डिस्क के केंद्र के गुजरे। डिस्क के शेष भाग का डिस्क के लम्बवत उसके केंद्र से गुजरने वाली अक्ष के परितः जड़त्व आघूर्ण है।
View Solutionएक डिस्क और एक गोला, जिनकी त्रिज्याएँ समान परन्तु द्रव्यमान भिन्न है, समान उन्नतांश ( झुकाव ) और लम्बाई के दो आनत समतलों पर लुढ़कते हैं | इन दोनों पिंडों में से तली तक पहले कौन पहुँचेगा ?
View Solutionकिसी दृढ़ छड़ की लम्बाई L है और इसका द्रव्यमान नगण्य है | इसके दो विपरीत सिरों पर क्रमश : तथा द्रव्यमान के दो बिंदु - पिण्ड रखे गए हैं | इस छड़ को उसके स्वयं के लम्बवत अक्ष के परितः घूर्णन कराना है, यदि यह अक्ष छड़ पर स्थित किसी बिंदु P से होकर गुजरती है ( आरेख देखिए), तो बिंदु P की वह स्थिति जिसके लिए छड़ को कोणीय वेग `omega_(0)` से घूर्णन कराने के लिए आवश्यक कार्य न्यूनतम होगा, है

View Solutionकिसी बिंदु `r=2hati-6hatj-12hatk` पर एक बल, `F=alphahati+3hatj+6hatk` लग रहा है, तो `alpha` के किस मान के लिए मूल बिंदु के परितः कोणीय संवेग संरक्षित रहेगा ?
View Solutionएक मोटर वाहन किसी सड़क पर `"54 km h"^(-1)` की चाल से चल रहा है | इसके पहियों की त्रिज्या 0.45 m है और घूर्णन अक्ष के परितः पहिए का जड़त्व आघूर्ण 3 kg m है | यदि ब्रेक लगाने के बाद, वाहन को रुकने में 15 s का समय लगता है, तो ब्रेक द्वारा पहिए पर लगा औसत बल - आघूर्ण का मान होगा
View Solutionएक छड़ का भार w है | यह दो समान्तर क्षुरधारों ( नाइफ एजों ) A तथा B पर टिकी है और क्षैतिज अवस्था में संतुलन में है | यदि A तथा B के बीच की दूरी 'd' है तथा छड़ का द्रव्यमान केंद्र A से x दूरी पर है तो , A पर अभिलम्ब प्रतिक्रिया का मान होगा
View Solutionm द्रव्यमान का एक पिण्ड ( वस्तु ), `R_(0)` त्रिज्या के पथ में किसी चिकने क्षैतिज समतल के ऊपर `v_(0)` वेग से गति कर रहा है | यह पिण्ड एक डोरी ( रस्सी ) से जुड़ा है | यह डोरी समतल पर बने एक चिकने छिद्र से होकर गुजरती है जैसा कि आरेख में दर्शाया गया है | इस डोरी पर तनाव को धीरे - धीरे बढ़ाया जाता है, जिससे अंत में यह पिण्ड `(R_(0))/(2)` त्रिज्या के वृत्ताकार पथ पर गति करने लगता है , तो गतिज ऊर्जा का अंतिम मान है
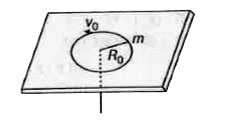
View Solutionतीन सर्वसम गोलीय कोशों ( खोखले गोलों ) में प्रत्येक का द्रव्यमान m तथा त्रिज्या r है | इन्हें आरेख में दर्शाए गए अनुसार रखा गया है | XX' एक अक्ष है, जो दो गोलीय कोशों को स्पर्श करती है और तीसरे के व्यास से होकर गुजरती है, तो XX' अक्ष के परितः इन तीन कोणीय कोशों के निकाय का जड़त्व आघूर्ण होगा
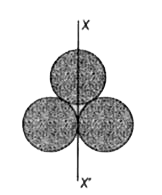
View Solution50 किग्रा द्रव्यमान तथा 0.5 मी त्रिज्या का एक ठोस सिलेण्डर ( बेलन ) अपनी क्षैतिज अक्ष के परितः स्वतन्त्र रूप से पोर्शन कर सकता है | इस पर एक भारहीन रस्सी लपेटी गई है, जिसका एक सिरा एक सिलेण्डर से जुड़ा है और दूसरा सिरा मुक्त रूप से लटक रहा है | रस्सी में कितना तनाव लगाया जाए कि कोणीय त्वरण `"2 परिक्रमण से"^(-2)` हो ?
View Solutionकिसी नत समतल का आनत कोण `theta` है | इस पर m द्रव्यमान तथा r त्रिज्या का एक ठोस गोला ऊपर से नीचे की ओर इस प्रकार गति करता है कि प्रथम दशा में गति पूर्णत : लोटनिक है और फिसलन नहीं है, तथा दूसरी दशा में गति केवल फिसलन है, और लोटनिक नहीं है, तो इन दोनों दशाओं में गोले के त्वरणों का अनुपात होगा
View Solutionद्रव्यमान M तथा लम्बाई L की एक छड़ PQ, P सिरे से लटकी हुई है | छड़ को क्षैतिज रखने के लिए इसे Q बिंदु पर द्रव्यमान रहित डोरी से बाँध दिया जाता है | जब डोरी को काट दिया जाता है, तब प्रारम्भ में छड़ का कोणीय त्वरण है

View Solutionएक छोटा कण, जो एकसमान घनत्व रखता है, प्रारम्भिक वेग v' से वक्र सतह पर ऊपर की ओर लुढ़कता है | यदि वह उच्चतम ऊँचाई `3v^(2)//4g` तक पहुँचता है, तब वस्तु है
View Solutionएक वृत्ताकार मंच एक घर्षणरहित ऊर्ध्वाधर धुरी पर टिका है | इस मंच की त्रिज्या `R = 2` मी और इसका जड़त्व आघूर्ण `"200 किग्रा - मी"^(2)` है | प्रारम्भ में यह विरामावस्था में है | 50 किग्रा द्रव्यमान का एक व्यक्ति इस मंच के किनारे पर खड़ा होता है और किनारे - किनारे ( अनुदिश ) भू - तल के सापेक्ष 1 मी/से के वेग से चलना प्रारम्भ करता है, तो इस व्यक्ति द्वारा एक चक्कर पूरा करने में लगा समय होगा
View Solutionकिसी एकसमान वृत्ताकार डिस्क ( चकती ) का जड़त्व आघूर्ण अधिकतम होगा, यदि घूर्णन अक्ष डिस्क के लम्बवत हो और वह गुजरती हो
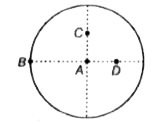
View Solutionविभिन्न द्रव्यमानों के तीन पिण्ड X- अक्ष पर इस प्रकार रखे हैं - 300 ग्राम का पिण्ड मूल बिंदु पर, 500 ग्राम का, x = 40 सेमी पर तथा 400 ग्राम का x = 70 सेमी पर हो, तो मूलबिंदु से द्रव्यमान केंद्र की दूरी होगी
View SolutionABC एक समबाहु त्रिभुज है, जिसका केंद्र O है | `F_(1),F_(2)` तथा `F_(3)` क्रमश : AB, BC तथा AC दिशा में लगे बल हैं | यदि O के पारित : कुल बल आघूर्ण शून्य हो, तो f`F_(3)` का मान होगा
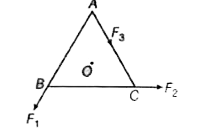
View Solutionचित्रानुसार एक कण डोरी से बाँधकर घर्षणरहित मेज पर घुमाते हैं | यदि डोरी को खींचकर डोरी के तनाव में वृद्धि कर दी जाए और डोरी को इतना खींचा जाए कि कण की चक्रीय घूर्णन त्रिज्या पहले से आधी हो जाए, तब कण की गतिज ऊर्जा
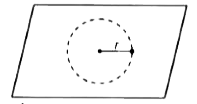
View SolutionM द्रव्यमान तथा L लम्बाई की एक पतली एकसमान छड़ का उसके अक्ष जो इसको लम्बाई के लम्बवत तथा इसकी लम्बाई के मध्य बिंदु से होकर गुजरती है, के पारित : बल आघूर्ण `I_(0)` है | इसके एक सिरे से गुजरने वाली तथा लम्बाई के लम्बवत अक्ष के पारित : जड़त्व आघूर्ण होगा
View Solutionएक घूर्णन करते पहिए पर एक तात्कालिक बिंदु की स्थिति `theta(t)=2t^(3)-6t^(2)` समीकरण से दी गई है | कितने समय पश्चात पहिए का बल - आघूर्ण शून्य होगा ?
View Solutionएक चकती की त्रिज्या R तथा द्रव्यमान 9M है, इससे द्रव्यमान M तथा त्रिज्या `R/3` की एक छोटी संकेन्द्रीय चकती पृथक कर दी जाती है शेष चकती का इसके केन्द्र से गुजरने वाले तथा तल के लम्बवत् अक्ष के परितः जड़त्व आघूर्ण है
View Solutionद्रव्यमान M तथा त्रिज्या r का पतला वृत्तीय वलय कोणीय वेग `omega` के साथ अपनी अक्ष : के पारित : घूर्णन करता है | यदि वलय के व्यास के विपरीत सिरों के बीच द्रव्यमान m के दो पिंडों को जोड़ दिया जाता है, तो वलय के घूर्णन करने पर कोणीय वेग होगा
View Solutionदो कण जो प्रारम्भ में विरामावस्था में हैं, आतंरिक आकर्षण के अंतर्गत एक - दूसरे की ओर गति करते हैं | यदि उन कणों की चाल किसी समय पर v तथा 2v हो, तब निकाय के द्रव्यमान केंद्र की चाल होगी
View Solutionएक कण का स्थिति वेक्टर `vecr` है और उसपर एक बल `vecF` लग रहा है। मूलबिंदु के परितः इस बल का आघूर्ण `vectau` है, तब
View Solution1 किग्रा तथा 3 किग्रा द्रव्यमान की दो वस्तुओं के स्थिति सदिश क्रमश : `hati+2hatj+hatk` तथा `-3hati-2hatj+hatk` हैं | इस निकाय के द्रव्यमान केंद्र का स्थिति सदिश है
View Solutionप्रत्येक द्रव्यमान M तथा लम्बाई L की चार समरूप पतली छड़ों से एक वर्गाकार फ्रेम बनाया जाता है | वर्ग के तल के लम्बवत तथा इसके केंद्र से गुजरने वाली अक्ष के पारित : इस फ्रेम का जड़त्व आघूर्ण
View Solutionएक वृत्तीय डिस्क और वृत्तीय रिंग, जिनका द्रव्यमान और त्रिज्या समान हैं, के अपने - अपने अक्ष के परितः परिभ्रमण त्रिज्याओं का अनुपात होगा
View Solutionलम्बाई L और द्रव्यमान M की एक पतली छड़ को अपने मध्य बिंदु पर `90^(@)` के कोण पर मोड़ा गया है | छड़ के मोड़ बिंदु से एक अक्ष इस तरह जाता है कि मुड़ी छड़ के दो भागों से बने तल से अक्ष लम्ब दिशा में है | इस अक्ष के परितः मुड़ी छड़ का जड़त्व आघूर्ण होगा
View Solutionl लम्बाई और m द्रव्यमान की एक अचर छड़ AB बिंदु A पर घूर्णन के लिए स्वतन्त्र है | क्षैतिज अवस्था में स्थित छड़ को स्वतन्त्र किया जाता है | A के सापेक्ष छड़ का जड़त्व आघूर्ण `(ml^(2))/(3)`है | छड़ का प्रारम्भिक कोणीय त्वरण होगा

View Solutionm द्रव्यमान का एक कण, XY तल में सीधी रेखा AB पर v वेग से गतिशील है | मूल बिंदु O के सापेक्ष कण का कोणीय संवेग बिंदु A पर `L_(A)`, हो तथा बिंदु B पर `L_(B)` हो, तो
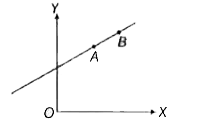
View Solutionएक एकसमान वृत्तीय चक्रिका की त्रिज्या R है और इसका द्रव्यमान M है | इस चक्रिका के व्यास के सिरे पर चक्रिका को छूती हुई चक्रिका तल से लम्ब दिशा के रेखा रूपी अक्ष के परितः चक्रिका का जड़त्व आघूर्ण होगा
View SolutionL लम्बाई की एक नली को एक असंपीड्य द्रव से पूरा भर कर इसे दोनों सिरों से बंद कर दिया गया है | बंद द्रव का द्रव्यमान M है | इस नली को एक क्षैतिज तल में नली के एक सिरे के परितः अचर कोणीय वेग `omega` से घुमाया जा रहा है | द्रव द्वारा नली के दूसरे सिरे पर क्रियाकारी बल होगा
View Solutionदो वस्तुओं का उनके घूर्णन - अक्ष के पारित : बल आघूर्ण क्रमशः I और 2I हैं | यदि इनकी घूर्णन गतिज ऊर्जाएँ बराबर हों, तो इनके कोणीय संवेगों का अनुपात होगा
View Solutionतीन कण जिसमें प्रत्येक का द्रव्यमान m ग्राम है, l सेमी भुजा वाले एक समबाहु त्रिभुज ABC के तीन शीर्षों पर स्थित हैं ( जैसा कि चित्र में दर्शाया गया है ) | ABC समतल में AB की लम्बवत रेखा AX के पारित : निकाय का जड़त्व - आघूर्ण `"ग्राम - सेमी"^(2)` में होगा
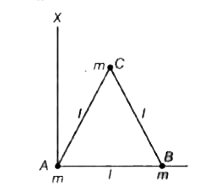
View Solutionसमतल के लम्बवत और केंद्र से निकलने वाले अक्ष के परित : एक गोल डिस्क का जड़त्व आघूर्ण `I_(2)` है | इसको एक दूसरी डिस्क के ऊपर रख गया है, जिसका जड़त्व आघूर्ण `I_(1)` है और यह `omega` कोणीय वेग से समान अक्ष के चारों ओर घूम रही है | डिस्कों के इस निकाय का अंतिम कोणीय वेग है
View Solutionकिसी वृत्ताकार डिस्क और समान त्रिज्या के वृत्ताकार रिंग के समतलों में स्पर्शज्या अक्षों के परितः घूर्णन त्रिज्याओं का अनुपात है
View Solutionएक निकाय में दो कण हैं , जिनका द्रव्यमान `m_(1)` और `m_(2)` हैं | यदि `m_(2)` द्रव्यमान वाले कण को द्रव्यमान केंद्र की ओर d दूरी तक धकेला जाता है, तो द्रव्यमान केंद्र को अपनी जगह पर ही रखने के लिए द्रव्यमान `m_(2)` वाले कण को कितनी दूर धकेला जाना चाहिए ?
View SolutionM द्रव्यमान और r त्रिज्या वाला एक पतला वृत्ताकार रिंग अपने अक्ष पर अचर कोणीय वेग `omega` से घूम रहा है | चार वस्तुओं जिनमें प्रत्येक का द्रव्यमान m है, को दोनों व्यासों के छोरों पर रखा गया है | रिंग का कोणीय वेग होगा
View Solutionद्रव्यमान M और R त्रिज्या वाला एक ठोस बेलन बिना फिसले नत समतल जिसकी लम्बाई L और ऊँचाई h है, पर लुढ़कता है | जब बेलन नीचे पहुँचता है, तो इसके द्रव्यमान केंद्र की चाल क्या है ?
View Solutionएक गेंद बिना फिसले लुढ़कती है | इसके द्रव्यमान केंद्र से गुजरने वाले अक्ष के परितः घूर्णन त्रिज्या k है | यदि गेंद की त्रिज्या R हो, तो इसकी घूर्णन ऊर्जा के साथ जुडी कुल ऊर्जा का अंश होगा
View Solutionएक लड़का अचानक एक वृत्तीय घूर्णी चकती पर आकर बैठ जाता है | क्या संरक्षित रहेगा ?
View SolutionR त्रिज्या का एक ठोस गोला एक क्षैतिज समतल पर रखा है | निम्न बिंदु से h ऊँचाई पर एक क्षैतिज बल F लगाया जाता है | द्रव्यमान केंद्र का त्वरण अधिकतम होगा, जब
View Solutionएक डिस्क दो समान द्रव्यमान की धातुओं ( एल्युमीनियम तथा लोहे ) से मिलकर इस प्रकार बनी है कि जिसका जड़त्व आघूर्ण अधिकतम है | यह तब संभव है जब
View Solutionयदि 3m लंबे छड़ का रेखीय घनत्व x के समानुपाती हो | जहाँ, x छड़ के एक सिरे से किसी बिंदु की दूरी है, इस सिरे से छड़ के गुरुत्व केंद्र की दूरी का मान होगा
View Solutionएक 1000 न्यूटन- मी का नियत बल - आघूर्ण किसी पिण्ड पर कार्य कर रहा है, जिसका उसके अक्ष के पारित: जड़त्व आघूर्ण `"200 किग्रा - मी"^(2)` है | 3 से बाद पिण्ड का कोणीय वेग होगा
View Solutionएक ठोस सिलेण्डर तथा खोखले सिलेण्डर समान द्रव्यमान तथा समान बाह्य व्यास के है | ये एक ही ऊँचाई से एक ही समय में नत समतल पर बिना फिसले नीचे गिराए जाते हैं | दोनों में से कौन पहले नीचे आता है ?
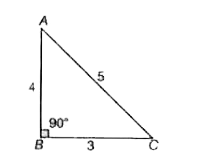
View Solutionएक त्रिभुजाकार पटल ABC है | AB = 4 सेमी , BC = 3 सेमी तथा `angleABC = 90^(@)` | यदि AB, BC तथा CA के परितः जड़त्व आघूर्ण `I_(1), I_(2)` तथा `I_(3)` है, तो निम्न में से कौन - सा कथन सत्य है ?
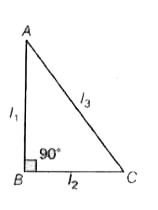
View Solutionएक M द्रव्यमान तथा R त्रिज्या वाली डिस्क का व्यास के समान्तर तथा परिधि के स्पर्शी अक्ष के परितः जड़त्व आघूर्ण होगा
View Solutionएक भारहीन 20 फुट लम्बी सीढ़ी एक दीवार पर ( क्षैतिज से ) `60^(@)` के कोण पर लगाई जाती है | 150 पाउण्ड का एक व्यक्ति सीढ़ी के उच्चतम बिंदु से 4 फुट पर खड़ा है | सीढ़ी को फिसलने के लिए कितने क्षैतिज बल की आवश्यकता होगी ?
View Solutionएक कार्बन मॉनोक्साइड अणु में कार्बन तथा ऑक्सीजन परमाणुओं के बीच की दूरी `1.12 xx 10^(-10)` मी है | कार्बन से द्रव्यमान केंद्र की दूरी है
View Solutionद्रव्यमान m, बल - आघूर्ण I तथा कोणीय चाल `(omega)` वाली वस्तु का कोणीय संवेग होगा
View Solutionएक फ्लाईवील 120 चक्कर/मिनट की दर से घूमता है | इसकी घूर्णन चाल होगी
View SolutionABC एक त्रिकोणीय प्लेट है | भुजाएँ चित्र में दी गई है | `I_(AB),I_(BC)` तथा `I_(CA)` क्रमश : `AB, BC` तथा CA अक्ष के परितः जड़त्व आघूर्ण है | निम्न में से कौन- सा सम्बन्ध सही है ?
View Solutionदो कारें द्रव्यमान m तथा 4m की हैं | ये r तथा 2r त्रिज्या के वृत्तीय पथ पर घूमती है | यदि ये एक ही समय में एक चक्कर पूरा लगा लेती हो, तो पहली कार तथा दूसरी कार की कोणीय चाल का अनुपात होगा
View Solutionएक इंजन का पहिया 90 चक्कर/मिनट से घूमता है | इसका कोणीय वेग होगा
View Solutionएक पहला छल्ला `30^(@)` के नत समतल पर नीचे आता है | इसमें रेखीय त्वरण का मान है
View Solutionएक बॉल, मेज पर बिना फिसले चलती है | कुल ऊर्जा का कितना भाग घूर्णन में लगेगा ?
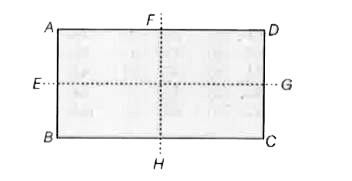
View Solutionएक आयत `ABCD(BC=2AB)` के किस अक्ष के परितः जड़त्व - आघूर्ण न्यूनतम होगा ?
View Solutionएक ठोस गोला h ऊँचाई के नत समतल पर बिना खिसके घूर्णन गति करता है | उसका रेखिक वेग होगा
View Solutionएक गोला घूर्णन गति करता है | रेखीय गतिज ऊर्जा तथा कुल गतिज ऊर्जा ( घूर्णन गतिज ऊर्जा सहित ) का अनुपात होगा
View Solutionएक फ्लाईवील अपने अक्ष के पारित : 360 J की घूर्णन गतिज ऊर्जा से घूमता है | कोणीय वेग 30 रेडियन/से है | इसका इसी अक्ष के परितः जड़त्व आघूर्ण होगा
View Solutionकिसी अक्ष के पारित : किसी पिण्ड का जड़त्व आघूर्ण `"1.2 किग्रा-मी"^(2)` है | आरम्भ में, पिण्ड स्थिर है | इसमें 1500 J की घूर्णन गतिज ऊर्जा बनाने के लिए 24 रेडियन/से का त्वरण लगाना पड़ता है | समय होगा
View Solutionएक ठोस सिलेण्डर का द्रव्यमान m तथा त्रिज्या r है | यह एक h ऊँचाई के नत समतल पर घूर्णन गति करते हुए नीचे आता है | इसके द्रव्यमान केंद्र की चाल क्या होगी, जब यह नीचे आ जाता है ?
View Solution
MCQs questions and complete solutions for chapter कणों के निकाय तथा घूर्णन गति of NEET PREVIOUS YEAR of Class 12