Complete Solutions to प्रश्न of chapter दोलन of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | दोलन |
| NEET PREVIOUS YEAR | प्रश्न |
| Number Of Questions | 54 |
| Academic Year | 2023-24 |
एक कण x अक्ष की दिशा में चलता हुआ सरल आवृत गति करता है तो बल होगा
View Solutionएक कण पर रेस्टोरिंग बल उसके विस्थापन के समानुपाती है तथा घर्षण बल उसके वेग के समानुपाती है जबकि उस पर F sin `omega` t का बल कार्य करता है। यदि कण का आयाम `omega=omega_(1)` पर अधिकतम हो तथा कण की ऊर्जा `omega=omega_(2)` पर अधिकतम हो तो
View Solutionएक m द्रव्यमान की वस्तु श्रेणीक्रम में जुड़ी हुई `K_(1)` और `K_(2)` बल नियतांको की स्प्रिंगो से लटकी हुई है। वस्तु कां दोलनकाल होगा
View Solutionसमान आवर्तकाल, एक दूसरे से `90^(@)` के कोण पर तथा `pi` कलान्तर की दो सरल आवर्तगतियों के संयोजन से कण का विस्थापन होता है
View Solutionएक सरल लोलक का आयाम तथा कोणीय वेग क्रमशः a तथा `omega` है। माध्य स्थिति सेx दूरी पर इसकी गतिज ऊर्जा T तथा स्थितिज ऊर्जा V है तो T तथा V का अनुपात होगा
View Solutionएक पिण्ड सरल आवर्तगति करता है। जब उसका विस्थापन माध्य स्थिति से 4 सेमी तथा 5 सेमी हो तो उसका वेग 10 सेमी / सेकंड तथा 8 सेमी / सेकंड है, तो इसका आवर्तकाल होगा
View Solutionएक सरल लोलक एक क्षैतिज दिशा में 'a' त्वरण से चलती हुई ट्राली की छत से लटका है। उसका आवर्तकाल `T=2pisqrt(l)/(g)` से दिया जाता है जहां g का मान होगा
View Solutionसरल आवर्त गति करते हुए पिण्ड का विस्थापन 0.02मीटर हो तो उसका त्वरण 2 मी/सेकंड`"^(2)` होता है। इसकी कोणीय आवृत्ति होगी
View Solutionएक सरल आवर्तगति करते हुए कण का आयाम A तथा आवर्तकाल T है। x-A से x A/2 तक चलने में लगा समय होगा
View Solutionएक कण आयाम A के साथ सरल आवर्तगति करता है। माध्य स्थिति से कितनी दूरी पर उसकी स्थितिज ऊर्जा कुल ऊर्जा की एक चौथाई है?
View Solutionनिम्न में से कौन-सी गति सरल आवर्तगति होगी
View Solutionएक कण दो परस्पर लम्बवत् सरल आवर्त गतियाँ इस प्रकार करते हैं कि इसके x तथा y अक्ष इस प्रकार दिये जाते है
`x=2 sin omegat , y = 2 sin A(omegat+(pi)/(4))`
कण का पथ होगा
View Solutionएक सरल आवृत्ति गति में जब विस्थापन आयाम का चौथाई होता है तो बताओ कुल ऊर्जा का कितना भाग गतिज ऊर्जा होगा?
View Solutionएक सरल आवृर्त दोलनचित्र में बल `2x× 10^(6)` न्यूटन/मीटर आयाम 0.01 मीटर तथा कुल ऊर्जा 160J हैं, तो
View Solutionएक कण अपनी माध्य स्थिति में सरल आवृत्त गति करता है। इसका A तथा आवर्तकाल T है। जब उसका वेग अधिकतम वेग का आधा हो तो उस समय विस्थापन ज्ञात करो
View Solutionयदि सरल लोलक की लम्बाई 2% बढ़ा दी जाए तो उसका आवर्तकाल
View Solutionदो सरल आवृत्तगति एक दूसरे के लम्बवत् है अर्थात् एक x- अक्ष में तथा दूसरा y- अक्ष में है। यदि दोनों का आयाम समान तथा कलान्तर ` pi//2` हो तो पथ होगा
View Solutionधातु से बने एक खोखले गोले में पानी भर कर एक लम्बे धागे से लटकाया गया है। उसमें एक सूक्ष्म छिद्र पेंदे में किया गया है जिससे पानी धीरे-धीरे रिसता है। यदि अब गोले को दोलन कराया जाये तो उसका आवर्तकाल
View Solutionदो सरल लोलकों की लम्बाई 5मीटर तथा 20 मीटर है। इनमें छोटा सरल रेखोग विस्थापन एक ही समय तथा एक ही दिशा में है। ये फिर एक ही कला में होंगे जब छोटी लम्बाई वाले लोलक ने ……..दोलन पूरे करे?
View Solutionएक सरल लोलक का आवर्तकाल 2सेकंड हैं। यदि इसका लम्बाई 4 गुणा कर दी जाए तो इसका आर्वतकाल होगा
View Solutionएक कण 0.01 मीटर आयाम तथा 60 हर्टज आवृत्ति की सरल आवर्तगति करता है। कण का अधिकतम त्वरण होगा:
View Solutionदो द्रव्यमान `M_(A)` तथा `M_(B)` को दो तारों, जिनकी लम्बाइयां `L_(A)` तथा `L_(B)` है, से लटकाने पर सरल आवर्तगतियां करते है। यदि इनको आवर्तियों में संबंध `f_(A)=2f_(B)` हो तो
View Solutionएक कण पर दो सरल आवर्तगतियां है। ये है- `x= A cos (omegat+delta),y=A cos (omegat+alpha)` जब `delta=alpha+(pi)/(2)` तो परिणामी गति होगी-
View Solutionएक सरल लोलक में एक धातु का लोलक इस्तेमाल किया गया है जो ऋणावेशित है। यह एक धनावेशित प्लेट के ऊपर दोलन करता है तो इसका आवर्तकाल
View Solutionएक कण m द्रव्यमान का है। वह 'a' आयाम की सरल आवृतगति करता है। उस पर Falkox का बल लगता है। कण की कुल ऊर्जा किस पर निर्भर करेगी ?
View Solutionएक m द्रव्यमान का पिण्ड ऊर्ध्वाधरत सरल आवर्तगति करता है। जब द्रव्यमान को स्प्रिंग A से लटकाया जाता है तो उसका आवर्तकाल `t_(1)` तथा B से लटकाने पर आवर्तकाल `t_(2)` है। यदि A तथा B को दिये गये चित्र की तरह जोड़ा जाए तो आवर्तकाल दिया जाता है
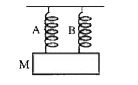
View Solutionएक सरल लोलक का आयाम वास्तविक आयाम का 1/3 भाग हो जाता है जब वह 100 दोलन पूरे कर लेता है। जब वह 200 दोलन पूरे कर लेता है तो उसका आयाम S भाग हो जाता है जहां S का मान होगा
View Solutionएक कण आयाम 'a' से सरल आवतंगति करता है। इसकी स्थिति ऊर्जा अधिकतम होगी जब यह माध्य स्थिति से दूर होगा
View Solutionद्रव्यमान m का एक कण दो बिन्दुओं `x_(1)` व `x_(2)` के बीच सरल आवर्त गति में कम्पन करता है, साम्य स्थिति O है, तो इसकी स्थितिज ऊर्जा का ग्राफ होगा:
View Solutionएक सरल आवर्त गतिक कम्पक की स्थितिज ऊर्जा कितनी होगी, जब कण अपने अंत्य बिंदु के आधे रास्ते पर है:
View Solutionएक स्प्रिंग से लटके द्रव्यमान का आवर्तकाल T है। यदि स्प्रिंग को चार बराबर भागों में बांट दिया जाए व समान द्रव्यमान को किसी एक भाग से लटकाये तो आवर्तकाल होगा:
View Solutionसरल आवर्त गति करते एक कण की चाल v तथा त्वरण a के लिए, तिम्नलिखित में से कौन-सा कथन सत्य है?
View Solutionबल नियतांक `k_(1)` व `k_(2)` वाली दो स्प्रिंगो को श्रेणी क्रम में जोड़ा गया है। संयोग का प्रभावी बल नियतांक है:
View Solution5 सेमी आयाम को सरल आवर्त गति करते एक कण की अधिकतम चाल 31.4 सेमी./से है। इसके कम्पन की आवृत्ति है
View Solutionजब एक लम्बे स्प्रिंग को 2 सेमी खींचा जाता है तो इसमें संचित स्थितिज ऊर्जा U होती है। यदि इसे 8 सेमी खोंचा जाए तो इसमें सोचत स्थितिज ऊर्जा होगी:
View Solutionएक कण सरल आवर्ती गति में है। इसके तात्क्षणिक वेग और त्वरण का कलान्तर होगा
View Solutionएक कण सरल आवर्त गति में है। इसकी गतिज ऊर्जा `K_(0) cos^(2) omega t` है। इसकी स्थितिज ऊर्जा और सम्पूर्ण ऊर्जा के क्रमानुसार अधिकतम मान होंगे
View Solutionएक ऊर्ध्व दिशा की कमानी को धरातल पर चित्र के अनुसार स्थायी किया गया है तथा इसके ऊपरी सिरे के पलड़े पर 20 किग्रा द्रव्यमान की वस्तु रखी है। कमानी और पलड़े के भार नगण्य हैं। थोड़ा दबाकर छोड़ देने पर द्रव्यमान सरल आवर्ती गति करता है। कमानी का बल नियतांक 200 न्यूटन/मी है। आवर्त गति का न्यूनतम आयाम कितना होना चाहिए, जिससे ऊपर रखी वस्तु पलड़े से अलग हो जाये ?
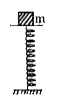
View Solutionएक कण आयाम के साथ सरल आवर्ती दोलन करता है। इसका दोलनकाल T है। इस कण को अपनी साम्य अवस्था से आयाम की आधी दूरी चलने में लगने वाला कम से कम समय होगा
View Solutionदो सरल आवर्त गतियाँ जिनकी कोणीय आवृत्तियाँ 100 और 1000 रैडियन प्रति सेकेण्ड हैं, समान विस्थापन आयाम रखती हैं। उनके अधिकतम त्वरणों का अनुपात होगा
View Solutionएक बिन्दु सरल आवर्त दोलन करता है जिसका आवर्तकाल T और चलन का समीकरण `x=asin (omegat+pi//6)` है। आवर्तकाल के किस अंश के पश्चात् बिन्दु का वेग उसके अधिकतम वेग का आधा होगा ?
View Solutionएक सरल लोलक x=0 के परितः सरल आवती चाल से चल रहा है जिसका आयाम और समय अन्तराल T है | `X=(a)/(2)` पर लोलक की चाल होगी :-
View Solutionनिम्न समीकरणों में से कौन सी सरल आवर्ती चाल को सूचक है:
View Solutionकिसी कण का x अक्ष के अनुदिश विस्थापन `x=a sin^(2) omegat` से दिया जाता है। इस कण की गति है।
View Solutionकिसी नगण्य द्रव्यमान के स्प्रिंग से लटकाये गये M द्रव्यमान का दोलनकाल T है। यदि इसके साथ ही एक अन्य M द्रव्यमान लटका दिया जाय तो दोलनकाल हो जायेगा
View Solutionकोई कण x-y समतल में `x=a sin omegat` तथा `y=a cos omegat` के अनुसार गति करता है। कण का पथ होगा
View Solutionदो तरंगों को क्रमशः `y_(1)=asin (omega t+kx + 0.57)` m तथा `y_(2) = a cos (omega t + kx)` m, से निरूपित किया जाता है, जहाँx मीटर में और सैकण्ड में है, तो दोनों तरंगों के बीच कलान्तर है:
View Solutionएक कण का द्रव्यमान है। इसे विराम अवस्था से मोचित किया गया है और यह आरेख में दिखाये गये अनुसार एक परवलीय मार्ग पर चलता है। यह मानते हुए कि कण का मूल स्थिति से विस्थापन कम है, कौन से ग्राफ कण की स्थिति को समय के फलन के रूप में सही दर्शाता है?
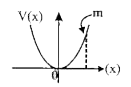
View Solutionकिसी कण को प्रदर्शित करने वाले निम्नलिखित फलनों में कौन से फलन सरल आवर्त गति को निरूपित करते है?
(a) `y=sin omega t- cos omega t`
(b) `y= sin^(3) omegat`
(c )`y=5 cos ((3pi)/(4)- 3 omegat)` (d) `y=1+omegat+omega^(2) t^(2)`
View Solutionदो कण, एक दूसरे के निकट स्थित दो समान्तर सरल रेखाओं के अनुदिश, समान आवृति और आयाम से दोलन कर रहे हैं। जब उनका विस्थापन उनके आयाम का आधा ( 1/2 ) होता है तो वे एक दूसरे से विपरीत दिशा में गति कर रहे होते हैं। दोनों कणों की माध्य स्थिति, उनके मार्गों की लम्बवत् एक सरल रेखा पर स्थित है। तो कलान्तर है
View Solutionकिसी दोलित्र पर अवमन्दन बल वेग के समानुपाती होता है तो समानुपाती नियतांक का मात्रक है
View Solutionकिसी सरल आर्वत तरंग का समीकरण `y=3 sin (pi)/(2) (50t-x)`
जहाँx तथा y मीटर में और सेकंड में है तो अधिकतम कण-वेग तथा तरंग वेग का अनुपात होगा
View Solutionकिसी पिण्ड (वस्तु) के चिकेने क्षैतिज पृष्ठ (सतह) पर दोलनों के समीकरण को `X - A cos (omega t)` द्वारा निरूपित किया जाता है, जहां
X=t समय पर विस्थापन `omega`= दोलनों की आवृत्ति
तो t के साथ a के विचलन (परिवर्तन) को कौन-सा ग्राफ (आलेख) सही रूप में दर्शाता है ?
View Solutionसरल आवर्त गति करते हुए किसी कण का अधिकतम त्वरण `alpha` तथा अधिकतम वेग `beta` है तो इसके कम्पन का आवर्तकाल होगा:
View Solution
प्रश्न questions and complete solutions for chapter दोलन of NEET PREVIOUS YEAR of Class 12