Complete Solutions to बहुविकल्पीय प्रश्न of chapter विद्युत आवेश तथा क्षेत्र of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | विद्युत आवेश तथा क्षेत्र |
| NEET PREVIOUS YEAR | बहुविकल्पीय प्रश्न |
| Number Of Questions | 38 |
| Academic Year | 2023-24 |
बिन्दु आवेश + 4q, -qतथा +4q,x-अक्ष के बिन्दु x =0,x=a,x= 2a पर रखे गये हैं।
View Solutionएक आवेश q दो आवेशों +Q को जोड़ने वाली रेखा के मध्य बिन्दु पर रखा गया है। ये तीनों आवेश संतुलन में होंगे यदि q का मान है:
View Solutionएक वैद्युत द्विध्रुव दो आवेशों `2 xx 10^(-6)` C से बना है। इनके बीच की दूरी 3 सेमी तथा वैद्युत क्षेत्र तीव्रता `2 xx 10^(5)` N/ c है। द्विध्रव पर बल आघूर्ण ज्ञात करोः
View Solutionएक वैद्युत क्षेत्र E, x- अक्ष की दिशा में है। 0.2C के आवेश को 2 मीटर चलाने में (जबकि Eसे `60^(@)` पर लाया गया हो) कार्य 4J करना पड़ता है तो E का मानः
View Solutionकिसी द्विध्रुवं के लिए वैद्युत क्षेत्र E तथा दूरी r एक दूसरे से निम्न किस प्रकार से संबंधित है?
View Solutionएक घन (L भुजा वाले) के मध्य बिन्दु पर एक आवेश q रखा गया है। घन से निकलने वाला वैद्युत फ्लक्स होगाः
View Solutionएक द्विध्रुव दो समान तथा विपरीत आवेशों कोः
View Solutionएक बिन्दु आवेश से किसी दूरी पर एक बिन्दु A है। A पर वैद्युत क्षेत्र 500 वोल्ट/मीटर तथा विभवांतर 3000 वोल्ट है। बिन्दु आवेश से A की दूरी होगी:
View Solutionएक खोखले चालक गोले (r=2मी) को +`10m mu` C आवेश दिया जाता है तो उसके केन्द्र पर वैद्युत क्षेत्र की तीव्रता होगी:
View Solutionएक m द्रव्यमान तथा qआवेश का कण समान वैद्युत क्षेत्र E में गति करना शुरु करता है। कण द्वारा अर्जित गतिज ऊर्जा का मान जबकि वह दूरी y चल चुका होः
View Solutionएक बिन्दु आवेश Q को वैद्युत द्विध्रुव. के लम्बार्धक पर रखा जाता है। यदि Q की दूरी द्विध्रुव से 7 हो `(r gtgta)` तो Q समानुपाती होगा (जबकि p द्विध्रुव आघूर्ण है)
View Solutionएक दो आवेशों के बीच K वैद्युतशीलता वाला माध्यम भर दिया जाए, तो उनके बीच लगने वाला अधिकतम बल
View Solutionएक अर्द्धवृत्तीय चाप जिसकी त्रिज्या a है को आवेशित किया गया। रेखीय आवेश घनत्व `lambda` है। तो चाप के केन्द्र पर वैद्युत क्षेत्र तीव्रता का मान होगा :
View Solutionएक आवेश Q को एक घन के किनारे पर रखा जाता है। इसकी प्रत्येक फलक से निकलने वाला वैद्युत फ्लक्स होगा :
View Solution`500 mu C` आवेश तथा 10 सेमी लम्बे द्विध्रुव के कारण इसकी अक्ष पर एक आवेश से 20 सेमी दूर बिंदु पर वायु में वैधुत क्षेत्र की तीव्रता होगी
View Solutionएक द्विध्रुव का द्विध्रुव-आघूर्ण `vecP` तथा `vecE` है तो लगने वाला आघूर्ण होगा
View Solutionयदि एक `vecp` द्विध्रुव-आघूर्ण वाला द्विध्रुव एक समान विद्युतक्षेत्र `vecE` में रख दिया जाए तो इस पर कार्य करने वाला आघूर्ण है:
View Solutionएक `Qmuc` का आवेश घन के केन्द्र पर रखा है किसी एक फलक से निकलने वाला वैद्युत फ्लक्स होगाः
View Solutionएक इलैक्ट्रॉन हाइड्रोजन अणु के चारों ओर r त्रिज्या के वृत्तीय पथ पर गति करता है। इनके बीच लगने वाला कूलॉम बल `vecF` होगा:
View Solutionएक धन के केन्द्र पर q आवेश रखा है। इसके किसी एक फलक से निकलने वाला वैद्युत फ्लक्स होगाः
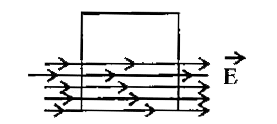
View Solutionएक वर्ग (भुजा=L मी) कागज के तल में है। एक वैद्युत क्षेत्र E कागज के तल में है तथा आधा वर्ग घेरता है। तो पृष्ठ से निकलने वाला वैद्युत फ्लक्स होगा :
View Solutionएक द्विध्रुव का आघूर्ण `vecp` को वैद्युत क्षेत्र `vecE` की दिशा में रखा गया है। द्विध्रुव को `90^(@)` घुमाने में किया गया कार्यः
View Solutionएक खोखले बेलन के भीतर कूलॉम का आवेश स्थित है। यदि चित्रानुसार वक्र तल B से सम्बद्ध वैद्युत अभिवाह वोल्ट मी मात्रकों में `phi` हो तो समतल तल A से सम्म वोल्ट-मी मात्रकों में अभिवाह होगा-

View Solutionतीन बिन्दुक आवेशों +q,-2q और +q को क्रमानुसार बिन्दुओं (x=0,y=a,z=0), (x=0,y=0, z=0) और (x=a,y= 0,z=0) पर रखा गया है। इस आवेश व्यवस्था के लिये वैद्युत द्विध्रुव आघूर्ण सदिश के मान और दिशा क्रमानुसार होंगे
View Solution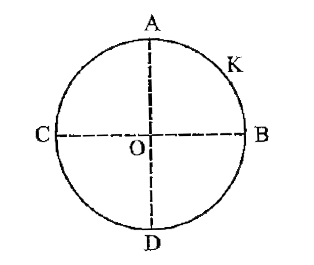
एक पतली विद्युत चालक R त्रिज्या की रिंग(छल्ले) को +Qआवेश दिया गया है। रिंग के केन्द्र 0 पर रिंग के भाग AKB के आवेश के कारण विद्युत फील्ड का मान E है। रिंग के शेष भाग ACDB के आवेश के कारण केन्द्र 0 पर विद्युत क्षेत्र का मान होगा :
View Solutionएक धातु में इलेक्ट्रानों का माध्य मुक्त पथ `4xx10^(-8)` m है। वह विद्युत-क्षेत्र जो धातु में किसी इलेक्ट्रॉन को औसत रूप में 2eV की ऊर्जा प्रदान कर सके, V/m की मात्रकों में होगा:-
View Solutionदो धन-आयनों के बीच की दूरी में है और प्रत्येक पर आवेश है। यदि इन दो आयनो के बीच का प्रत्याकर्षण बल F हो तो, प्रत्येक आयन में से कितने इलेक्ट्रॉन लुप्त (अविद्यमान) हैं। (e-एक इलेक्ट्रॉन का आवेश है)
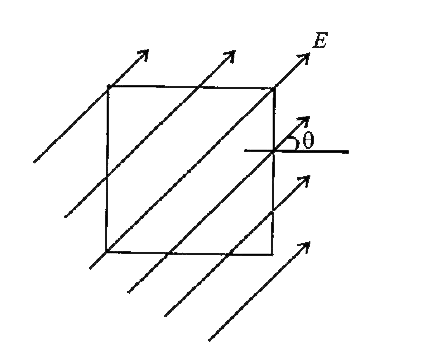
View SolutionL मीटर भुजा की एक वर्गाकार सतह, पेपर के समतल में, किसी एक समान विद्युत क्षेत्र में रखी है। विद्युत क्षेत्र की तीव्रता E (v/m) है और यह उसी समतल के अनुदिश, वर्ग की क्षैतिज भुजा से कोण पर कार्य करता है, जैसा की चित्र (आरेख) में दिखाया गया है। इस सतह से सम्बद्ध विद्युत फ्लक्स, volt. m में है
View SolutionR त्रिज्या के किसी आवेशित चालक गोलीय कोश (खोल) के केन्द्र से `(3R)/(2)` दूरी पर विद्युत क्षेत्र E है। इसके केन्द्र की `(R )/(2)` दूरी पर विद्युत क्षेत्र होगा
View Solutionदो समान्तर धातु की प्लेटें एक दूसरे के सामने कुछ दूरी पर रखी हैं। इन प्लेटों पर+Qऔर-Qआवेश हैं। यदि प्लेटों को केरोसीन के टैंक में डूबा दिया जाय तो उनके बीच विद्युत क्षेत्र
View Solutionएक आवेशQ, त्रिज्यार के किसी गाउसीय गोलीय पृष्ठ से परिबद्ध है। यदि त्रिज्या को दुगुना कर दिया जाए तो, बाहर की ओर विद्युत फ्लक्स:
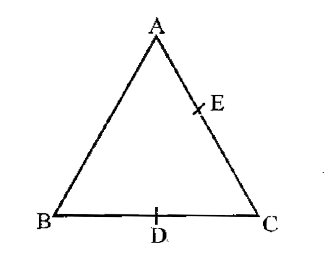
View Solutionएक समद्विबाहु त्रिभुज ABC की भुजा BC और AC,2aहै। इसके प्रत्येक कोने पर +qआवेश स्थित है। बिन्दु D और E क्रमशः भुजाओं BC और CA के मध्यबिन्दु है। तो Dसे E तक किसी आवेश को ले जाने में किया गया कार्य होगाः
View Solutionकिसी वर्ग के चार कोनों पर बिन्दु आवेश -Q,-q, 2q तथा 2Q क्रमशः रखे गये हैं। ए तथा q के बीच क्या संबंध होना चाहिये, ताकि वर्ग के केन्द्र पर विभव शून्य हो जाए.
View Solutionयदि 'a' भुजा के किसी घन के एक कोने पर एक बिन्दु आवेश व रखा जाए तो, इससे होकर जाने वाला फ्लक्स होगा :
View Solution1 cm तथा 3 cm त्रिज्या के धातु के दो गोलों को क्रमशः `-1xx10^(-2)` Cतथा `5xx10^(-2)` C, आवेश दिया गया है। यदि, इनको एक चालक तार से जोड़ दिया जाए तो, बड़े गोले पर अन्तिम आवेश होगा :
View Solutionसरकंडे (पिथ) की दो बॉलों (गोलियों) पर समान(बराबर) आवेश है। इन्हें समान लम्बाई की डोरियों (धागे) से एक बिन्दु से लटकाया गया है। संतुलन की अवस्था में इनके बीच की दूसरी 7 है। दोनों डोरियों को उनकी आधी लम्बाई पर कस कर बाँध दिया जाता है। अब संतुलन की स्थिति में दोनों बॉलों के बीच की दूरी होगाः

View Solutionयदि किसी क्षेत्र में विभव (वोल्ट में) V(x, y,z)=6xy y+2yz, से निर्दिष्ट किया जाये तो बिन्दु (1,1,0) पर विद्युत क्षेत्र (N/C में) है:
View Solutionकिसी उभयनिष्ठ बिन्दु से, लम्बाई । की दो द्रव्यमानहीन डोरियों से निलंबित, दो सर्वसम आवेशित गोले, अन्योन्य प्रतिकर्षण के कारण, आरम्भ में एक-दूसरे से d `(dltlt1)` दूरी पर हैं। दोनों ही गोलों से एक नियत दर से आवेशों का क्षरण आरम्भ होता है, और इसके परिणामस्वरूप गोले एक दूसरे की ओर वेग v से आते हैं। तब गोलों के बीच की दूरी, x के फलन के रूप में वेग v का विचरण किस रूप में होता है?
View Solution
बहुविकल्पीय प्रश्न questions and complete solutions for chapter विद्युत आवेश तथा क्षेत्र of NEET PREVIOUS YEAR of Class 12