Complete Solutions to Exercise of chapter INTRODUCTORY NOTES of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | INTRODUCTORY NOTES |
| NN GHOSH | Exercise |
| Number Of Questions | 27 |
| Academic Year | 2023-24 |
A current element of 2 milliampere meter is at the corner. A of a unit cube ABCDEFGH, the element being along AB. Calculate the field at the remaining seven corners of the cube (figure 1.5).
View SolutionTwo currrent elements `2 xx 10^(-4)` A m and `5 xx 10^(-4)` Am are placed at the vertices A and B of an equilateral triangle along AB in the same sense. Calculate the magnetic field at C. (Each side of the triangle measures 10 cm)
View SolutionFour corner elements of length 0.01 cm carrying `10^(-3)` A lie at the four corners of a square ABCD along AB, BC, CD and DA. Calculate the magneti field at the centre of the square. Each side of the square =10 cm.
View SolutionA current elemetns of 0.2 A m is fixed at the centre of a circle of radius 10 cm . Another element of strength 0.5 A m is placed along the circumference and moved round the circle. At which positions will they sent maximum force on each other? Calculate these forces.
View SolutionTwo current elements of strength 0.2 A m and 0.4 A m from a cross at the centre of a circle of radius 10 cm Calculate the magnetic field at a point on the circle `30^(@)` away (anticlockwise) from the first element.
View Solutioncalculate the force experinced by an electron when it enters a uniform magnetic field of strength 2 T with vleocity `0.2 xx 10^(8) m s^(-1)` at right angles to the field. What kind of motion will it have in the magnetic field ? (Charge of electron `1.6 xx 10^(-19)` coulomb.)
View SolutionAn electron of velocity `2 xx 10^(6) m s^(-1)` is moving in magneitc field of strength 1 T making an angle `45^(@)` with it. Find the magnitude and direction of the magnetic force experienced by it. Charge of electron`=1.6 xx 10^(-19)` C.
[ Hint : `vec F=q_(0)vec vxx vec B`.]
View SolutionA ball of mass `2 xx 10^(-3)` kg carries a charge of `2 xx 10^(-8)` C. This ball is given an initial horizontal velocity of `5 xx 10^(4) ms^(-1)` in the earth's gravitational field. What is the magnetic field required to keep the ball moving without deflection ?
[Hint : `F_(m)` (magnetic force) `=q_(0)vB "sin"theta=omegag`]
View SolutionThe plane of a rectangular coil of wire of dimensions `0.05 xx 0.10m` and carrying a current of 10 A ,is parallel to a magnetic field of 0.1 T . What is the torque on the coil? What will be the torque when the normal to the coil makes an angle of `30^(@)` with the direction of the field ?
View SolutionConsidering `theta=pi//2` as the zero-energy position of a current loop of magnetic moment m placed in a magnetic field of strength B,find the minimum potential energy. In what position is the potential energy minimum? Is this an equilibrium position ? What will be the work done in turning it through `alpha` from this position ? Examine whether you get the dame position for equilibrium and same value for work if `theta=0` is taken as the zero-energy position.
View SolutionA ring of dielectric material, with a total charge +q distributed uniformly over its surface, rotates with angular speed `omega.` Find the magnetic moment of the ring .Compare its magnetic moment with its angular momentum , assuming that its mass is m.
View SolutionA this disc of dielectric material, with a total charge +q distributed uniformly over its surface, rotates with angular speed `omega` about an axis perpendicular to the disc and passing through its centre .Find the magnetic moment with its angular momentum , assuming that its mass is m.
[Hint : Consider a ring of radius x and thickness dx. Calculate charge on it and then the current consituited by its rotation .Find its magnetic moment and integrate for the whole disc.]
View SolutionElectric charge +q is iniformaly distributed over the entire volume of a sphere of radius r. Calculate the magnetic moment of the sphere if it spins about its diameter with angular speed `omega` . Compare this moment with its angular momentum, assuming that its mass is m.
View SolutionAn insulated wire is wound so that it forms a flat coil with N=100 turns. The radius of the innermost turns is `R_(1)=4 cm` . What magnetic moment will this coil have when a current of I=10 mA flows in it ?
View SolutionApply Ampere's solenoid in terms of linear density of turns n and current I.
View SolutionApply Ampere's circuital law to determine the magnetic induction inside a thick wire of radius R and carrying I amperes of current.
View SolutionIn a device called electronmagnetic pump for transferring molten metals ,a rectangular pipe is placed in a uniform magneitc field B perpendicular to its axis and one of the sides of the section and a strong current I in then passed perpendicular to both B and the axes of the pipe . The molten metal is then passed through the pipe . What is the guage pressure produced by the pump ?
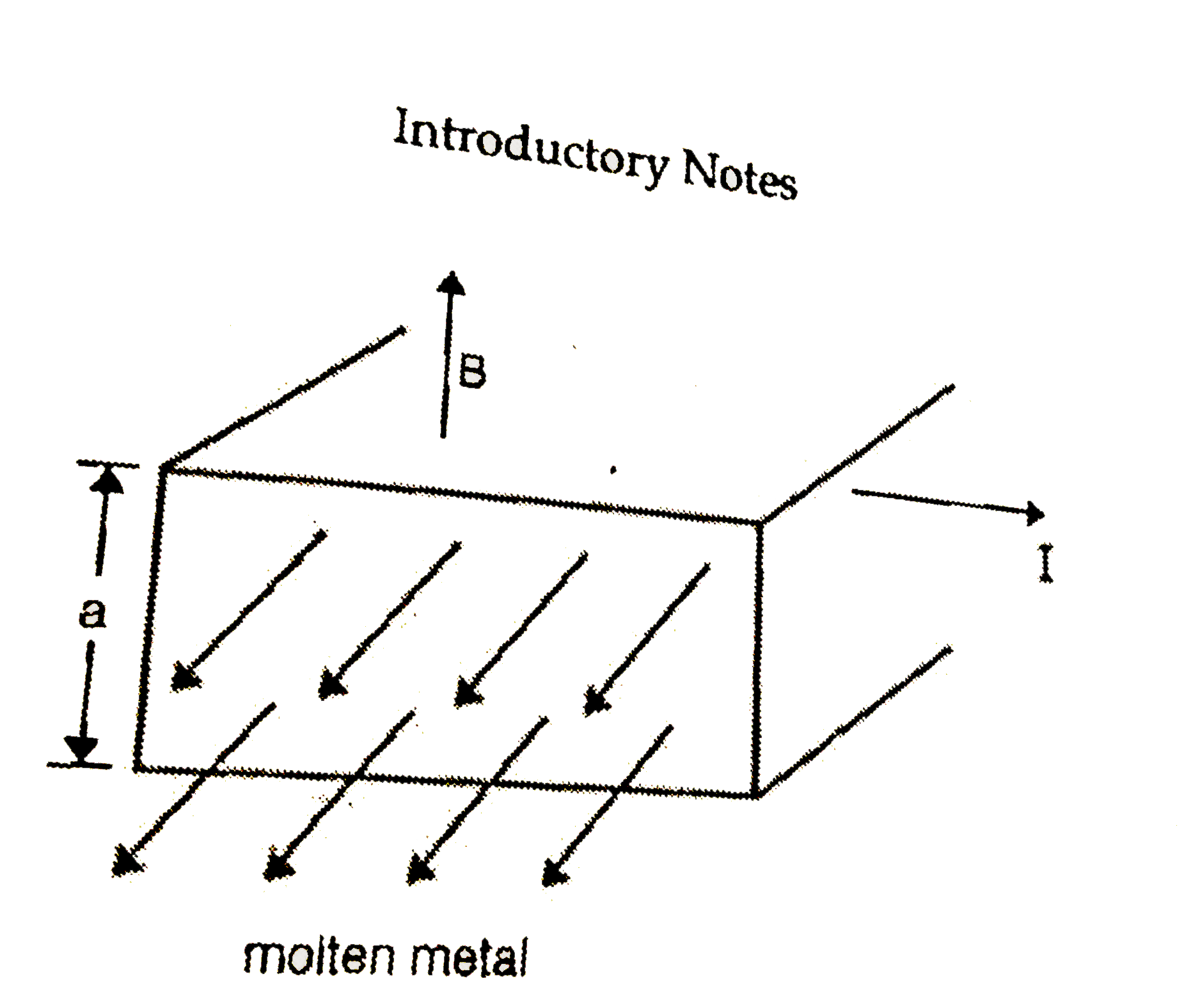
View SolutionA current `I` flows in a long thin walled cylinder of radius `R`. What pressure do the walls of the cylinder experience ?
View SolutionA current `I` flows in a long single layer solenoid with cross-sectional radius `R`. The number of turns per unit length of the solenoid equals `n`. Find the limiting current at which the winding may ruputure if the tensile strength of the wire is equal to `F_(l i m)`.
View SolutionWhat pressure does the lateral surface of a long straight solenoid with n turns per unit length experience when a current I flows through it.
View SolutionFind the magntiude and diraction of the magnitude induction vector `B`
(a) of an infinite palne carrying a current of linear density I, the vector `i` is the same at all points of the plane,
(b) of two parallel infinite planes carrying currents of linear densities a dn -1, the vectors `i` and `-i` are cohnstant at all points of the corresponding planes.
View SolutionA unifrom current of density `f` flows inside an infinite plate of thickness `2d` parallel to its surface . Find the magentic induction induced by this current as a funcition of the distance `x` from the median palane of the plate. The magnitude permeability is assumed to be equal to unity both inside and outside the plates.
View SolutionA long horizontal wire `AB`, which is free to move in a vertical plane and carries a steady current of `20 A`, is in equilibrium at a height of `0.01 m` over another parallel long wire `CD` which is fixed in a horizontal plane and carries a steady current of ` 30 A`, as shown in figure. Shown that when `AB` is slightly depressed, it executes simple harmonic motion. Find the period of oscillations.

View SolutionA wide copper strip of width l is bent into piece of slendder tubing of radius R with two plane extension as shown (Fig. 1.12). A current I flows through the strip, distributed uniformly over its width. Ib this way, one-turn solenoid has been formed (a) Derive an expression for the magnetic field in the tubular part.
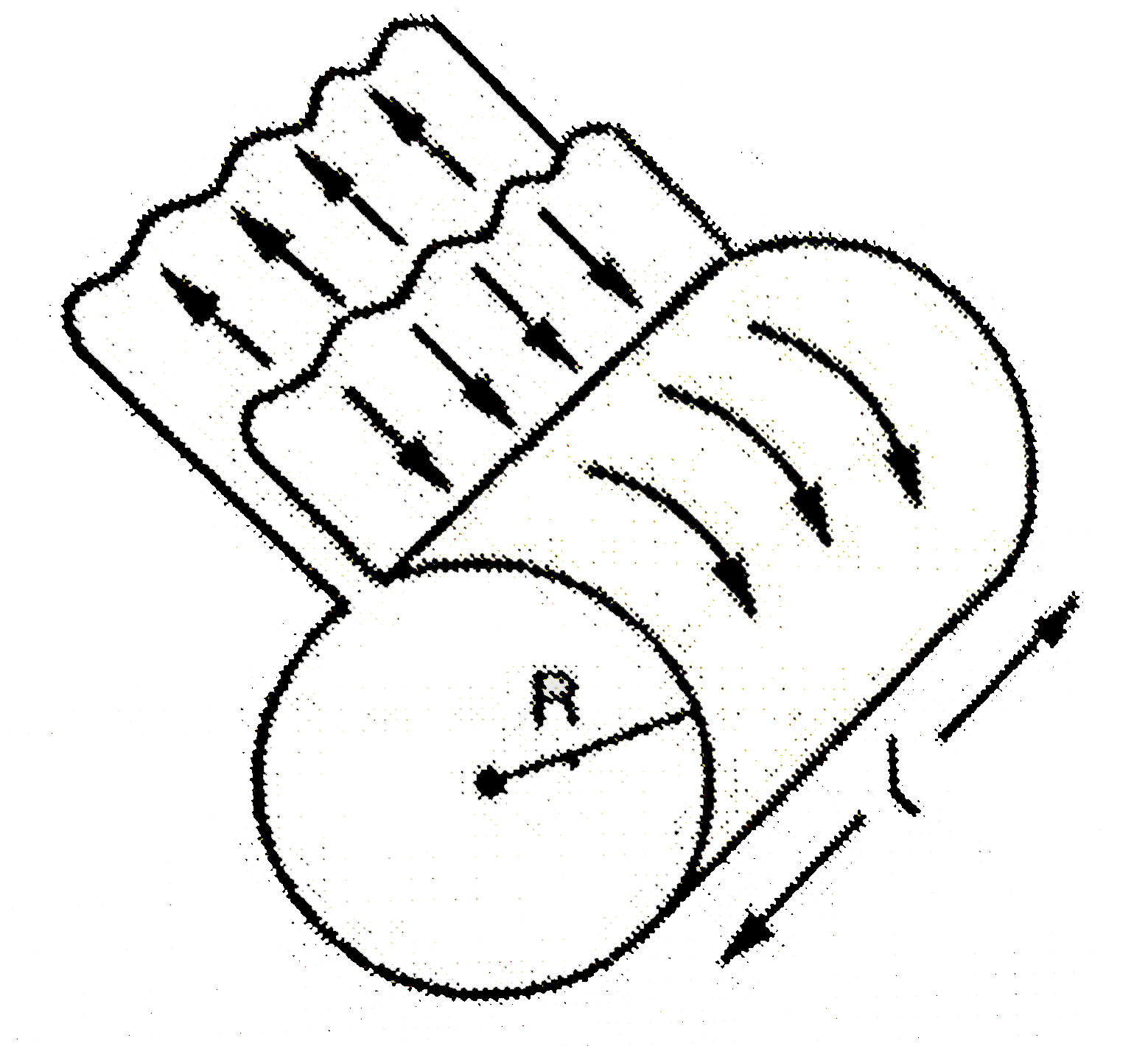
View SolutionFigure shows a cross-section of a long ribbon of width `omega` that is carrying a uniformly distributed total current i into the page. Calculate the magnitude and direction of the magnetic field `B` at a point `P` in the plane of the ribbon at a distance d from its edge. `

View SolutionThe current density `bar(J)` inside a long, solid cylindrical wire of radius `a = 12 mm` is in the direction of the central axis, and its magnitude varies linearly with radial distance r from the axis according to `J = (J_(0) r)/(a)`, where `J_(0) = (10^(5))/(4 pi) A//m^(2)`. Find the magnitude of the magnetic field at `r = (a)/(2)` in `mu T`
View SolutionA long cylindrical conductor of radius a contains a long cylindrical holr of radius l. The axes of the two cylinders are parallel and are at a distance d apart. A current I is uniformly distributed over the cross-section. Find the magnetic field at the centre of the hole.
[Hint: Apply the principle of superposition of magnetic field]
View Solution
Exercise questions and complete solutions for chapter INTRODUCTORY NOTES of NN GHOSH PHYSICS (HINGLISH) of Class 12