Complete Solutions to EXAMPLE B of chapter HEATING AND CHEMICAL EFFECT OF CURRENT of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | HEATING AND CHEMICAL EFFECT OF CURRENT |
| NN GHOSH | EXAMPLE B |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
A 2 m long wire of resistance `4 Omega` and diameter 0.64 mm is coated with plastic insulation of thickness 0.66 mm. A current of 5A flows through the wire. Find the temperature difference across the insulation in the steady state. Thermal conductivity of plastic is `0.16 xx (10^-2) cal//s cm.^@C`.
View SolutionA fuse made of lead wire has an area for cross-section `0.2mm^(2)`. On short circuiting will the fuse wire reaches 32 A. How long after the short circuiting will the fuse begin to melt? For lead, specific heat capacity `134J kg^(-1)K^(-1)`, melting point =`327^(@)C`, relative density =11.34, initial temperature =`20^(@)C` electricaL resistivity `=11xx10^(-8)Omegam`.
View SolutionAn electric kettle has two windings. When one of the n is switched on the kettle begins to boil in `t_(1)` minutes and when the other is switched on it begins to boil in `t_(2)` minutes. In what time will the kettle begin to boil if both windings are switched on simultaneously in series and a parallel?
View SolutionA shortage battey with an emf of 10V and an internal resistance `1Omega` is connected across an extenal resistance R and liberates of 9W power. Find the potential difference across the teminals of the battery and the value or values of R.
View SolutionA copper voltameter is connecterd in series with a battey and a `1Omega` coil. The current is passed for an hour and the increasae in weight of the cathode is 2.952g. The reading of the voltmeter connected across `1-ohm` coil is 2.5V. Calculate E.C.E. of copper.
View SolutionA metal plate with a total surface are of `300cm^(2)` is to be benickel plate. If a current of 1.5A is used for 3 hours, find the thickness of nickel deposited. (Density of nickel `=8800 kgm^(-3), "E.C.E. of a nickel" 30.4xx10^(_8) kg C^(-1)`.
View SolutionA copper voltameter is connected in series with a tangent galvanometer of 10 turns and 5cm in radius. Calculate the weight of copper is deposited in 30 minutes if the deflection of the galvanometer is `60^(@)`. (Horizontal component of earth's field `=28A m^(-1)and "E.C.E of copper" =32.8 xx 10^(-8)kgC^(-1)`.
View SolutionIn copper voltameter 20mg of copper is deposited on the cathode of the voltameter by `0.15-wedge` current in 6minutes 42sec. Calculate (i) amount of electricity required to liberate one gram equivalent of any substance, (ii) charge carried by an electron. (Atomic mass of copper =64l Avogardo constant=`=6.02xx10^(23)"mol"^(-1)` and copper is divalent.)
View SolutionA steady current is passed for 25minutes through a silver voltameter and ammeter in series and 0.059g of silver of deposited. The ammeter reads 0.3A. Find the errror, if any, in the ammeter reading, given that the E.C.E. of silver `=11.18xx10^(-7) kg C^(-1)`.
View SolutionA current of 5A is passed fir 5hours through three voltameters arranged in series, containing solution of copper sulphate. Silver nitrate and sulphuric acid. Calculate the masses of silver, copper and hydrogen liberated (E.C.E of silver `=11.18xx10^(-7) kg C^(-1)`m=, atomic weight of silver =107.88, atomic weight of copper =63.57 and atomic weight weight of hyrdrogen=1.008.)
View SolutionA current passes throgugh a copper voltameter and water voltameter I series. How much hydrogen at `27^(@)C` and pressure of 100cm of mercury wil be liberated during the time it takes for 17.5g of copper to be deposited? (Atomic weight of copper=63 and density of hydrogen at S.T.P.=`0.09 kg m^(-3)`.
View SolutionWhen a detonating gas explodes, 34.5kcal ar liberted per gram of hydrogen. Use this observation to ding the minimum emf of a battery at which the electrolysis of water is possible. (A faraday=96,500C.)
View SolutionA cell develops the same power across two resistances `R_(1)` and `R_(2)` separately. The internal resistance of the cell is
View SolutionA series battery by 6 lead accumulators each of emf 2.0V and intenal resistance `0.5Omega` is charged by a 20V d.c. supply, What series resistance should be used in the charging, circuit in order to limit the current to 1A. Calculate the power sullpied by the source and the fraction of energy stored in the battery.
View SolutionA dynamo of emf `varepsilon_(1)=120V` and internal resistance `r=0.5Omega`, and a storage battery of `varepsilon_(2)=110V` are connected to an extenal resistance R. At what maximum value of R will there be no current through the storage battery? How will be the battery operate when the resistance R is large or smaller than the calculated value?
View SolutionA Capacitor of capacitance `C=5muF` is connected to source of emf `varepsilon_(2)=200V` with the switch S in the position 1 (Figure 6.2). Subsequently the switch is pushed to the position2. Find the amount of heat generated in `R_(1)=500 Omega if R_(2)=300Omega`.
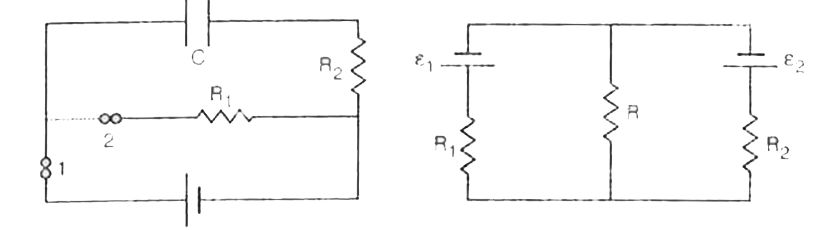
View SolutionIn the cirucit (figure6.3) resistance `R_(1) and R_(2)` are known and cells ar of emf `e_(1) and e_(2)` and negligible internal resistance. At what value of R will the thermal power generated in it be the highest? What is it equal to?
View SolutionA capacitor of capacitance C is charged to a voltage `V_(0)` and subsequently discharged through a combination of a resistor R and another identical capacitor C in series. Find the current at time t and heat generated in the same time.
View SolutionShow the Joule's law can be expressed as `Q=rhol^(2) or sigmaE^(2)` where Q is the heat generated per unit volume of the conductor, j=current density, `rho`=respectively of the material of the conductor, `sigma`=conductivity and E= electric field step up in the conductor.
View SolutionA coil of radius r=25cm is made of a thin copper wire of length l=500m and resistance R rotates with an angular velocity `omega=500m` and resistance R rotates with an angular velocity `omega=300 rad//sec` about its axis. Calculate the quantities of charges in the coil that will flow duie to the sudden stoppage of the coil
"["Hint: Loss in KE= Heat produced"]"
View SolutionWhat amount of heat will be generated in a coil of resistance `R` due to a charge q passing through it if the current in the coil
a. decreases down to zero uniformly during a time interval `t_0`?
b. decrases down to zero having its value every `t_0` seconds?
View SolutionA Perfect gas is enclosed in a vertical cylinder filled with a piston of mass m. The gas is heated by passing constant current I through a heating coil of resistance R placed inside the cylinder. At what speed v must the piston move upward in order that temperature of the gas may remain unchanges? Assume ideal insulating walls and piston and there is no fusion.
View SolutionA straight conductor of area of cross-section S and resistivity `rho` is connected to a ballistic galvometer. The conductor is moved with speed v and stoped suddenly. The ballistic gal=vom=nometer registors flow of q couloumbs of electricity Show that this observation can be used to measure `(e)/(m)` of electrons.
"["Hint: Orderly motion of elcctrons is throuwn into randon motion within relaxation time `tau`"]"
View Solution
EXAMPLE B questions and complete solutions for chapter HEATING AND CHEMICAL EFFECT OF CURRENT of NN GHOSH PHYSICS (HINGLISH) of Class 12