Complete Solutions to वस्तुनिष्ठ प्रकार प्रश्न of chapter कॉलम का नियम तथा वैद्युत क्षेत्र of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | कॉलम का नियम तथा वैद्युत क्षेत्र |
| KUMAR MITTAL | वस्तुनिष्ठ प्रकार प्रश्न |
| Number Of Questions | 16 |
| Academic Year | 2023-24 |
कल्पना कीजिए कि एक प्रोटॉन और एक इलेक्ट्रॉन के आवेश में अल्प अंतर होता है। इनमे से एक `-e` है और दूसरा`(e xx Delta e)` है। यदि एक दूसरे से 'd' दूरी पर रखे हाइड्रोजन के दो परमाणुओं के बीच (जहाँ d परमाणु के साइज से बहुत अधिक है) स्थिर वैद्युत बल और गुरुत्वीय बल का परिणामी (नैट) शून्य है तो `Delta e` कि कोटि होगी: (दिया है हाइड्रोजन का द्रव्यमान `m_(h) = 1.67 xx 10^(-27) kg`)
View Solution`[epsi_(0)]` निर्वात की वैद्युशीलता का विमीय सूत्र है। यदि M = द्रव्यमन, L = लम्बाई, T = समय तथा A = वैद्युत धारा, तब :
View Solutionदो बड़ी ऊर्ध्वाधर व समांतर धातु की प्लेटो के बीच 1 सेमी की दूरी है। वे X विभवांतर के D.C स्त्रोत से जुडी है। दोनों प्लेटो के बीच एक प्रोटॉन स्थिर अवस्था में छोड़ा जाता है। छोड़े जाने के तुरंत बाद प्रोटॉन ऊर्ध्वाधर से `45^(@)` कोण बनता हुआ गति करता है। तब X का मान लगभग है:
View Solutionकिसी उभयनिष्ठ बिंदु से, लम्बाई l की दो द्रव्यमानहीन डोरियों से निलंबित, दो सर्वसम आवेशित गोले, अन्योन्या प्रतिकर्षण के कारण, आरम्भ में एक-दूसरे से `d (d lt lt l)` दूरी पर है। दोनों ही गोलों से एक नियत दर से आवेशों का क्षरण आरम्भ होता हैऔर इसके परिणामस्वरूप गोले एक-दूसरे की ओर वेग v से आते है तब गोलों की बीच की दूरी x के फलन के रूप में वेग से v विचरण किस रूप में होता है?
View Solutionत्रिज्या r की एक पतली अर्ध्दवृत्ताकार वलय पर q धन-आवेश एकसमान रूप से वितरित है। केंद्र O पर नैट क्षेत्र E है:
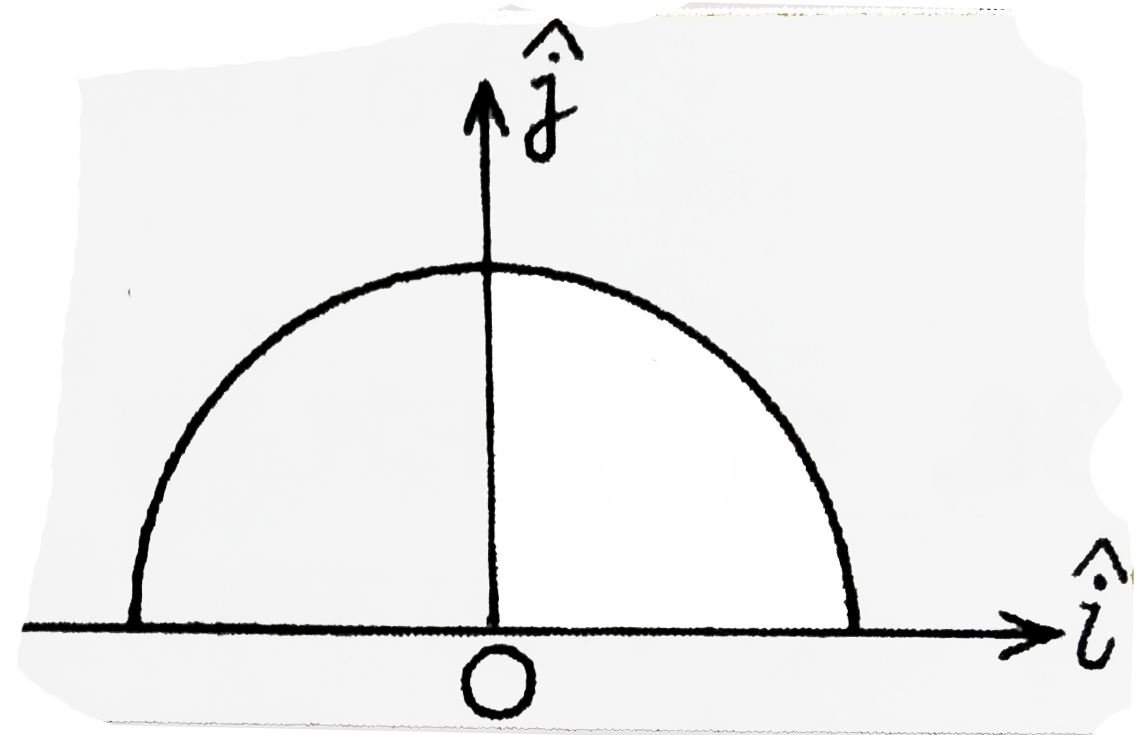
View Solutionदो आवेश जिनमे प्रत्येक q है X -अक्ष पर `x = - a` तथा `x = a` पर रखे गये है। एक कण जिसका द्रव्यमान m आवेश `q_(0) = (q)/(2)` है, मूल-बिंदु पर रखा गया है। यदि आवेश `q_(0)` को y -अक्ष के अनुदिश थोड़ा-सा विस्थापित `(y lt lt a)` कर दिया जाये तो कण पर कार्यरत नैट बल अनुक्रमानुपाती है:
View Solutionदो समान प्रकार के स्थिर आवेश जिनके परिमाण Q है परस्पर 2d दूरी पर रखे गये है। इनके बीच मध्य बिंदु पर एक कण जिसका द्रव्यमान M तथा आवेश q है, विरामावस्था में रखा है। निकाय चित्रानुसार समरेख है। कण को अब दोनों आवेशों को मिलाने वाली रेखा के अनुदिश थोड़ा-सा `x (x lt lt d)` विस्थापित कर छोड़ दिया जाता है। यह अब मध्य स्थिति के पारित: दोलन करता है, जिसका दोलन काल है:

View Solutionसमान परिमाण के तीन धन-आवेश एक समबाहु त्रिभुज के कोनो पर रखे गये है। परिणामी बल -रेखएं निम्नांकित रेखा-चित्रों में कौन-सी है?
View Solutionकिसी लम्बे बेलनाकार कोश के ऊपरी भाग में धनात्मक आवेश `sigma` तथा निचले भाग में ऋणात्मक पृष्ठ आवेश `-simga` है। इस बेलन (सिलिंडर) के चारो ओर वैद्युत क्षेत्र-रेखाये, यहाँ दर्शाये गये आरेखों में से किस आरेख के समान होगी। (यह आरेख केवल व्यवस्था आरेख है और स्केल के अनुसार नहीं है)
View Solutionसमान परिमाण के छ: आवेश जिनके तीन धनात्मक है तथा तीन ऋणात्मक है, एक षट्भुज के P, Q, R, S, T, U कोनो पर इस प्रकार रखे गये है की केंद्र O पर क्षेत्र उस क्षेत्र का दो गुना है जो बिंदु R पर केवल एक धन-आवेश रखने पर उत्पन्न होता। तब P, Q, R, S, T व U पर रखे आवेशों का क्रमश: क्रम होगा।
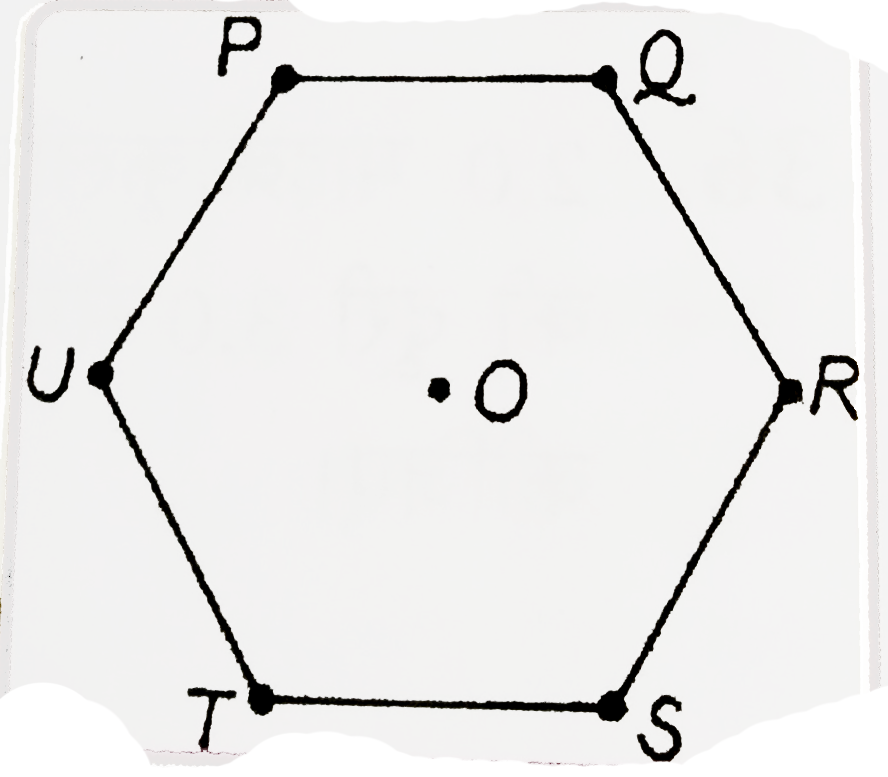
View Solutionद्रव्यमान `m_(e)` का एक इलेक्ट्रॉन एकसमान वैद्युत क्षेत्र E में विरामावस्था से चलकर `t_(1)` समय में एक निश्चित दूरी तय करता है। द्रव्यमान `m_(p)` का एक प्रोटॉन भी इसी एकसमान वैद्युत क्षेत्र में विरामावस्था से चलकर `t_(2)` समय में उतनी ही दूरी तय करता है। गुरुत्वीय प्रभाव को नगण्य मानते हुए, `t_(2)//t_(1)` का अनुपात लगभग है:
View Solutionदिये गये चित्रों में दो स्थितियाँ दर्शायी गई है जिनमे दो अनंत लम्बाई के एकसमान रैखिक आवेश घनत्व `lamda` (धनात्मक) के सीधे तार परस्पर समांतर रखे गये है। चित्रानुसार q तथा `-q` मान के दो बिंदु आवेश तारो से समान दूरी पर उनके वैद्युत क्षेत्र में साम्यावस्था में रखे हुये है। ये आवेश केवल X -दिशा में चल सकते है। यदि आवेशों को उनकी साम्यावस्था से थोड़ा-सा विस्थापित कराया जाये, तो सही विकल्प है:
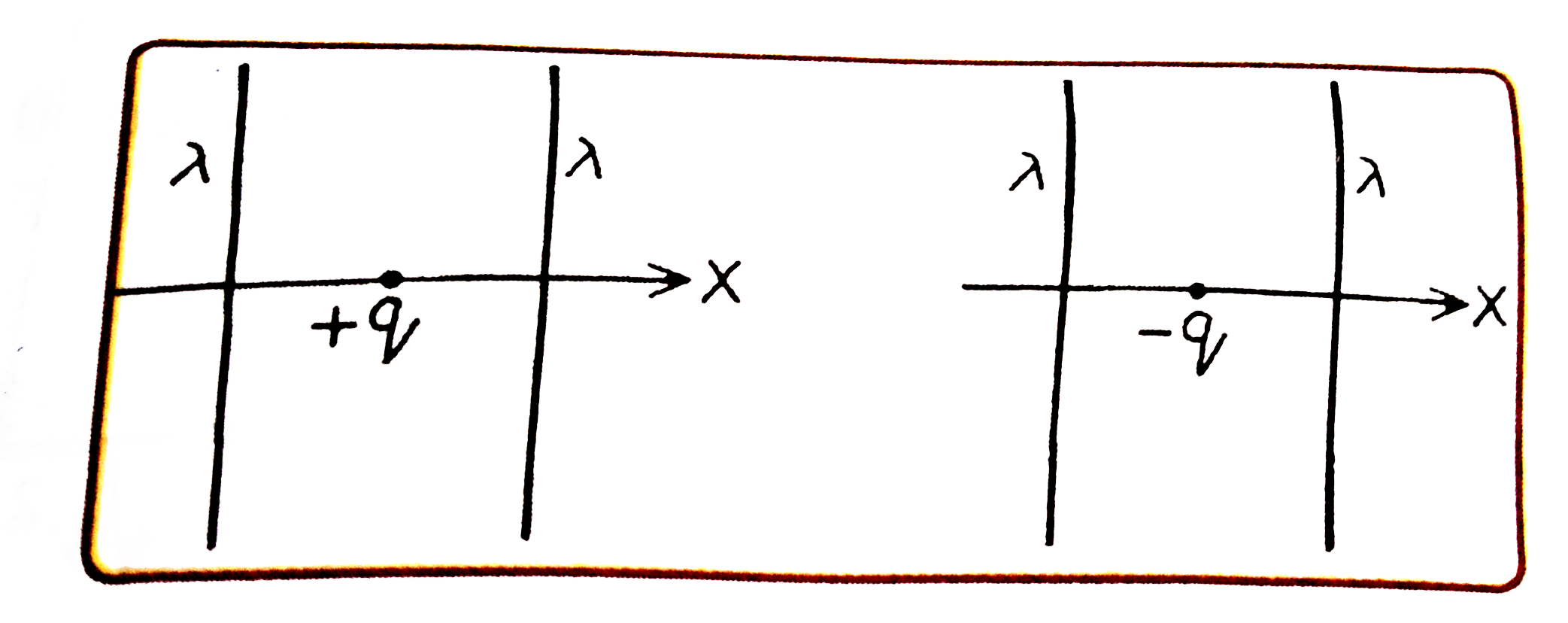
View Solutionतेल की एक लघु गोलीय बूँद जिस पर नेट आवेश q है, शांत वायु में `(81pi)/(7) xx 10^(5)` वाल्ट/मीटर तीव्रता वाले एक उध्र्वाधर एकसमान वैद्युत क्षेत्र में संतुलित है। जब क्षेत्र का स्विच बंद कर देते है तो बंद `2 xx 10^(-3)` क्रांतिक वेग मीटर/सेकंड से गिरती है। दिया है `g = 9.8` मीटर `"सेकंड"^(-2)` , वायु की श्यानता `= 1.8 xx 10^(-5)` न्यूटन-सेकंड `"मीटर"^(-2)` तथा तेल का घनत्व = 9000 किग्रा `"मीटर"^(-3)`, q का परिमाण है:
View Solutionएक वैद्युत द्विध्रुव को `2 xx 10^(5) N//C` तीव्रता के वैद्युत क्षेत्र से `30^(@)` कोण पर रखने के उस पर 4 N-m का बल-आघूर्ण लगता है। यदि द्विध्रुव की लम्बाई 2 सेमी हो, तो उस पर आवेश होगा:
View Solutionएक वैद्युत द्विध्रुव का स्थिर द्विध्रुव आघूर्ण `vec(P)` है जो कि X-अक्ष से `theta` कोण बनता है। वैद्युत क्षेत्र `vec(E)_(1) = E hat(i)` में रखने पर यह बल आघूर्ण `vec(tau)_(1) = tau hat(k)` का अनुभव करता है। वैद्युत क्षेत्र `vec(E)_(2) = sqrt3 E_(1) hat(j)` में रखने पर यह बल-आघूर्ण `vec(tau)_(2) = - vec(tau)_(1)` का अनुभव करता है। कोण `theta` का मान होगा:
View Solutionकोई इलेक्ट्रॉन विरामावस्था से किसी एकसमान तथा ऊपर को ऊर्ध्वाधर वैद्युत -क्षेत्र E में कोई दी गई दूरी, h गिरता है। अब वैद्युत-क्षेत्र का परिमाण अपरिवर्तित रखते हुए इसकी दिशा उत्क्रमित कर दी जाती है। किसी प्रोटॉन को विरामावस्था से इतनी ही ऊर्ध्वाधर दूरी h तक इसमें गिरने दिया जाता है। प्रोटॉन के गिरने में लिए गए समय की तुलना में इलेक्ट्रॉन द्वारा गिरने में लिया गया समय है:
View Solution
वस्तुनिष्ठ प्रकार प्रश्न questions and complete solutions for chapter कॉलम का नियम तथा वैद्युत क्षेत्र of NAGEEN PHYSICS (HINDI) of Class 12