Complete Solutions to विविध प्रतियोगी परीक्षाओ के लिए (वस्तुनिष्ठ प्रकार प्रश्न एकल उत्तर प्रकार) of chapter वैधुत विभव of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | वैधुत विभव |
| KUMAR MITTAL | विविध प्रतियोगी परीक्षाओ के लिए (वस्तुनिष्ठ प्रकार प्रश्न एकल उत्तर प्रकार) |
| Number Of Questions | 17 |
| Academic Year | 2023-24 |
एक आवेश Q लम्बाई L की छड़ AB के अनुदिश एकसमान रूप से वितरित है जैसा कि चित्र में दिखाया गया है । एक बिंदु O पर जो सिरे A से L दूरी पर है , वैधुत विभव है :

View Solutionबराबर परिमाण के धन तथा ऋण बिंदु-आवेश क्रमशः `(0,0,(a)/(2))` तथा `(0,0,-(a)/(2))` बिंदुओ पर रखे है । जब किसी अन्य बिंदु-आवेश को बिंदु (-a,0,0) से बिंदु (0,a,0) तक चलाया जाता है, तो वैधुत क्षेत्र द्वारा किया गया कार्य है :
View Solutionदो बिंदु P तथा Q क्रमशः 10 V तथा -4 V के विभवो पर पोषित (maintained )है । बिंदु P से Q की ओर 100 इलेक्ट्रॉन चलाने पर किया गया कार्य है :
View Solutionयहाँ आरेख में कुछ समविभव क्षेत्र दर्शाये गए है :
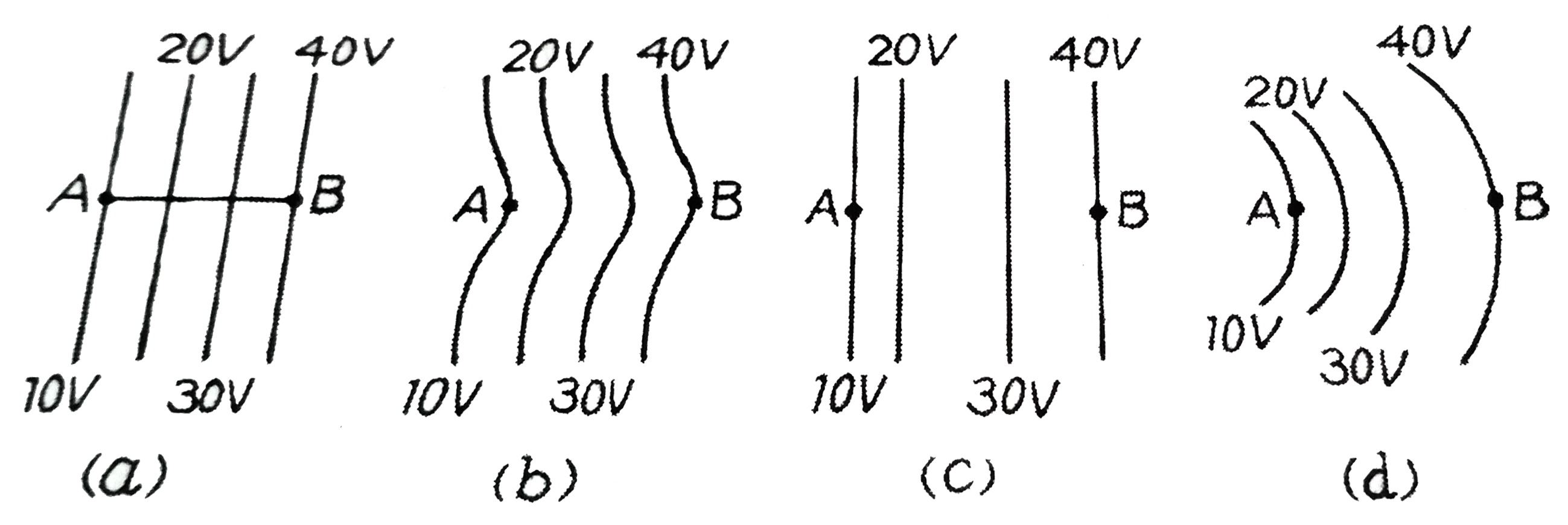
प्रत्येक आरेख एक धनात्मक आवेश को A से B तक ले जाते है । तो, इस प्रक्रम में , q को A से B तक ले जाने में :
View SolutionX-अक्ष पर `x=x_(0),x=3 x_(0), x=5 x_(0),..oo` के प्रत्येक बिंदु पर एक आवेश +q रखा है तथा `x=2 x_(0), x=4 x_(0), x=6 x_(0),..oo` के प्रत्येक बिंदु पर एक अन्य आवेश -q रखा है । `x_(0)` एक धन नियतांक है । माना कि आवेश Q के कारण r दूरी पर किसी बिंदु पर वैधुत विभव `Q//(4pi epsilon_(0) r)` है । तब, उपरोक्त आवेशों के निकाय के कारण मूल-बिंदु पर विभव है :
View Solutionकिसी क्षेत्र (region ) में धन X -दिशा में दिष्ट एकसमान वैधुत क्षेत्र लगा है । माना A मूल-बिंदु है । X -अक्ष पर x=+1 सेमी पर एक बिंदु B है तथा Y -अक्ष पर y=+1 सेमी पर एक बिंदु C है । तब बिंदुओ A , B तथा C पर विभव संतुष्ट करते है :
View Solutionमाना व्योम में एक वैधुत क्षेत्र `vec (E )=30 x^(2) hat(i) ` है तब विभवान्तर `V_(A)-V_(0)`, जहाँ `V_(0)` मूलबिंदु पर विभव एवं `V_(A),x=2` मीटर पर विभव है
View Solutionयदि किसी वैधुत क्षेत्र में विभव (वोल्ट में ) को, V(x,y,z)=6xy-y+2yz, से निर्दिष्ट किया जाये , तो बिंदु (1,1,0) पर, वैधुत क्षेत्र (न्यूटन/कूलॉम में) है :
View Solutionकिसी क्षेत्र में विभव को,V(x,y,z)=6x-8xy-8y+6yz से, निरूपित किया जाता है, जहाँ V, वोल्ट में तथा x,y तथा z मीटर में है । तो बिंदु (1,1,1) पर स्थित 2 कूलॉम आवेश पर लगने वाला वैधुत बल होगा :
View Solution0.5 मीटर त्रिज्या की एक अचालक वलय जिसकी परिधि पर असमान रूप से वितरित कुल आवेश `1.11xx10^(-10)` कूलॉम है, आकाश(space )में प्रत्येक स्थान पर वैधुत क्षेत्र `vec (E )` उत्पन्न करती है। वलय के केंद्र पर l=0 लेने पर, `int_(l=oo)^(l=0) - vec (E )* d vec (1)` रेखा-समाकल का वोल्ट में मान है
View Solutionदो समरूप पतली वलय जिनमे प्रत्येक की त्रिज्या R मीटर है, परस्पर समाक्ष रूप से (coaxially ) R मीटर की दूरी पर स्थित है । यदि दोनों वलयो पर क्रमशः `Q_(1)` कूलॉम व `Q_(2)` कूलॉम के आवेश समान रूप से वितरित है, तो q कूलॉम आवेश को एक वलय के केंद्र से दूसरी के केंद्र तक ले जाने में किया गया कार्य है :
View Solutionतीन संकेन्द्री धातु कोष A , B तथा C जिनकी त्रिज्याये क्रमशः a , b तथा `c(a lt b lt c)` है, पृष्ठ -आवेश-घनत्व क्रमशः `+sigma, -sigma` तथा `+sigma` है कोष B का विभव होगा :
View Solutionचित्र में प्रदर्शित `q_(1)= +2xx10^(-8)` कूलॉम तथा `q_(2)= -0.4xx10^(-8)` कूलॉम है । एक आवेश `q_(3)=0.2xx10^(-8)` कूलॉम को वृत्त की चाप के अनुदिश C से D तक चलाया जाता है । `q_(3)` की स्थितिज ऊर्जा
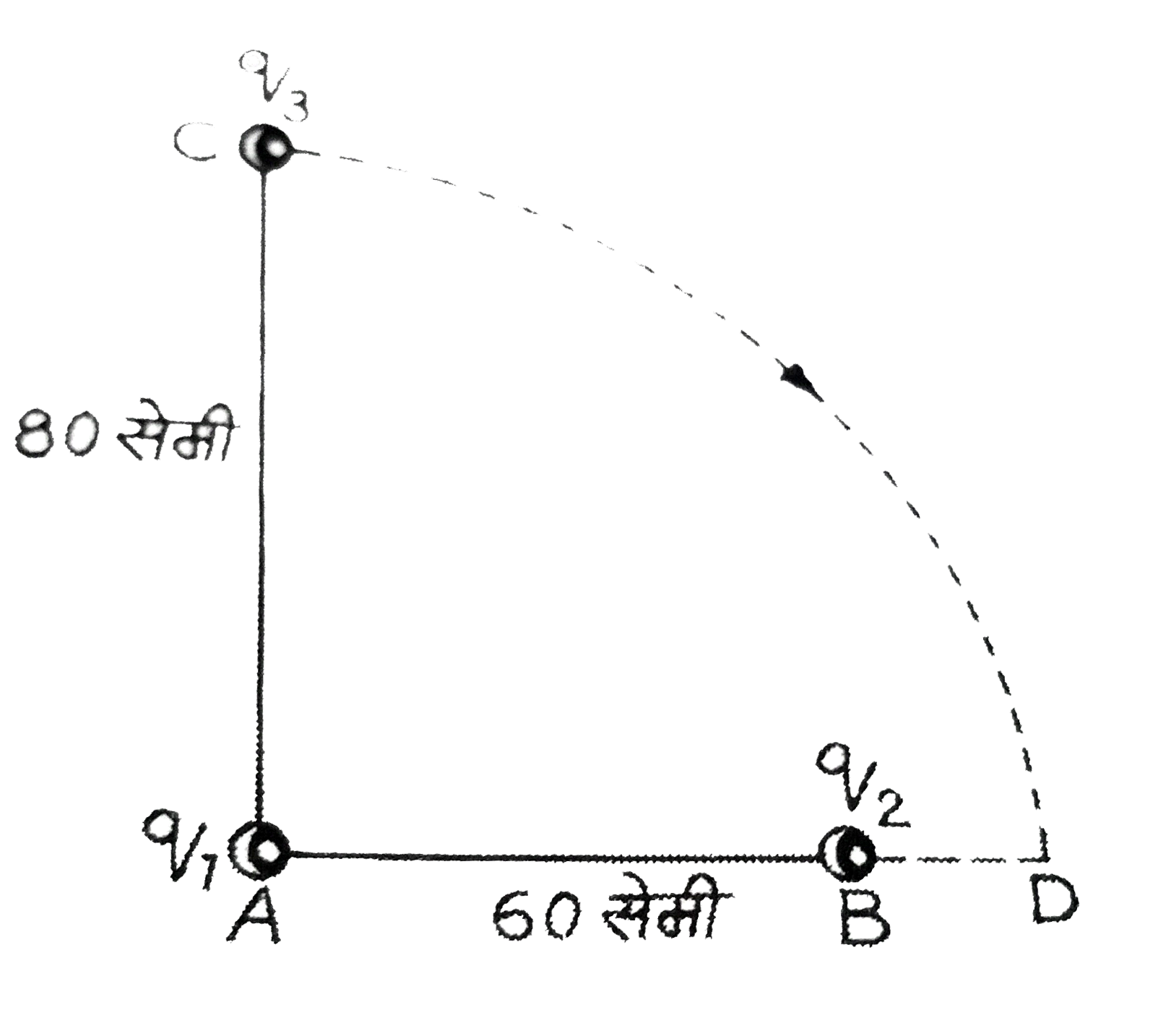
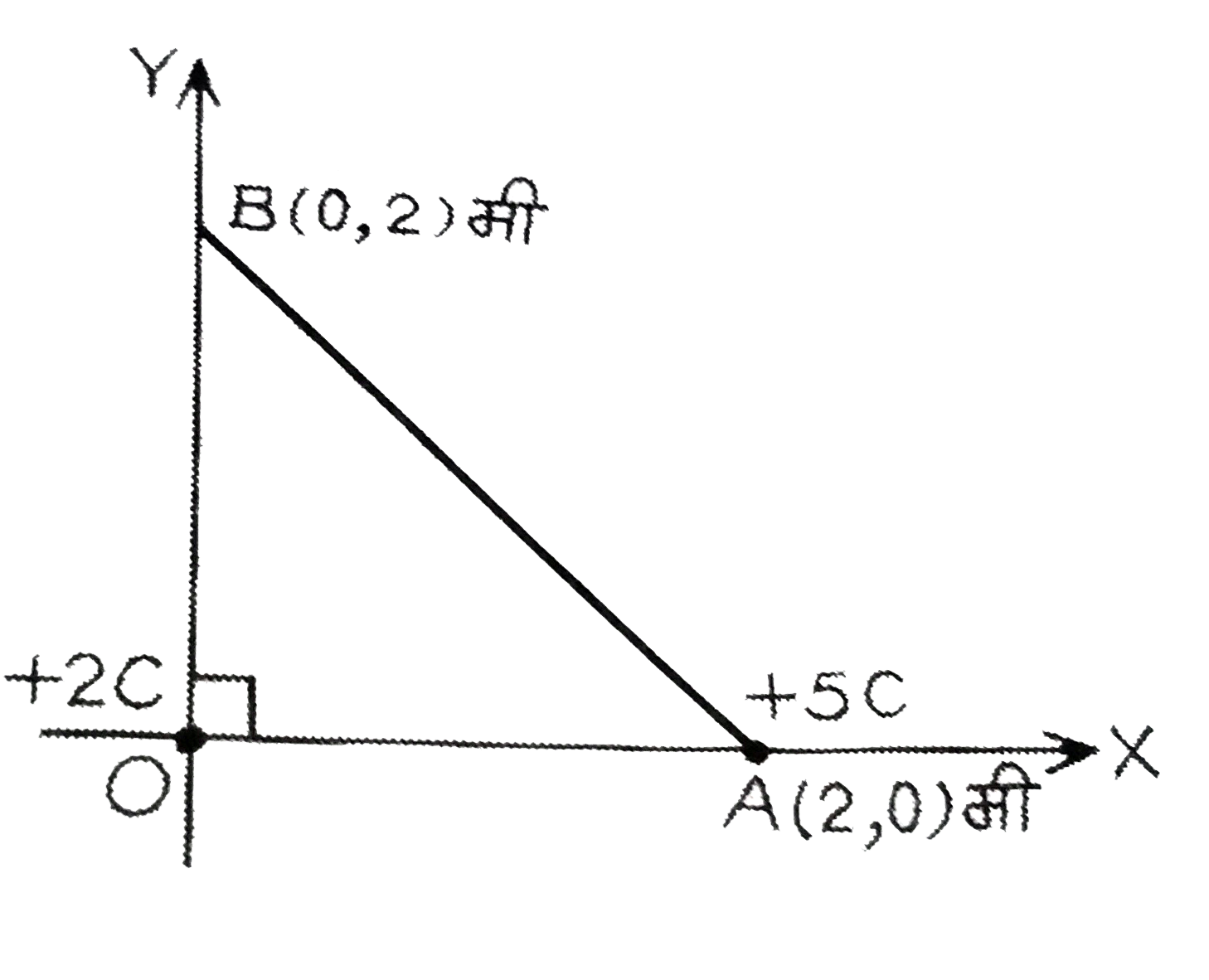
View Solutionचित्र में दिखाये गये अनुसार, एक आवेश +2C मूल बिंदु O पर स्थित है तथा एक अन्य आवेश +5C , X -अक्ष पर बिंदु A पर स्थित है । बाद का आवेश बिंदु A से Y -अक्ष पर बिंदु B पर लाया जाता है किया गया कार्य है
View Solutionदिये गए चित्र के अनुसार, एक समूह में रखे तीन आवेशों `(q)/(3),(q)/(3),-(2q)/(3)` के क्रमशः बिंदु A,B तथा C पर रखा गया है । त्रिज्या R वाले वृत्त का केंद्र-बिंदु O है तथा कोण `CAB =60^(@)`

View SolutionR त्रिज्या के एक पतले गोलीय कोश का केंद्र मूल-बिंदु पर है । इस पर धनावेश पृष्ठ -घनत्व एकसमान है । वैधुत क्षेत्र के मान E (r ) तथा वैधुत विभव V (r ) का केंद्र से दूरी r के साथ विचरण (variation )का सर्वोत्तम वर्णन किस ग्राफ में है ?
View Solutionएक चालक गोले की त्रिज्या R है । इस पर Q आवेश है । इस गोले के केंद्र पर वैधुत क्षेत्र क्रमशः होंगे :
View Solution
विविध प्रतियोगी परीक्षाओ के लिए (वस्तुनिष्ठ प्रकार प्रश्न एकल उत्तर प्रकार) questions and complete solutions for chapter वैधुत विभव of NAGEEN PHYSICS (HINDI) of Class 12