Complete Solutions to गणित of chapter JEE MAIN TEST-3 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | JEE MAIN TEST-3 |
| NTA MOCK TESTS | गणित |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
एक यादृच्छिक चर X का प्रायिकता बंटन निम्न रूप में दिया गया है:
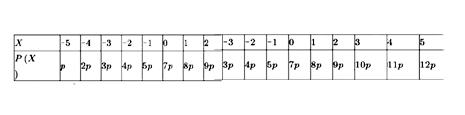
तब, p का मान है01:29View Solutionएक चक्रीय चतुर्भुज की दो आसन्न भुजाओं की लम्बाईयाँ 2 इकाई और 5 इकाई हैं और उनके बीच का कोण 60° है। यदि चतुर्भुज का क्षेत्रफल `4sqrt3` वर्ग इकाई है, तब चतुर्भुज का परिमाप है:
08:15View Solutionयदि f(x) = cos (log x), तब `f(x) f(y)-1/2 [f(x/y)+f(xy)]` का मान है
04:48View Solution`((sqrt(x))/(sqrt(3))+(sqrt(3))/(2x^(2)))^(10)` के प्रसार में x से स्वतन्त्र पद ज्ञात कीजिए।
03:18View Solution`y=xe^(|x|)` एवं रेखाओं |x|=1, y=0 द्वारा परिबद्ध क्षेत्रफल ज्ञात कीजिये।
03:42View Solutionवक्रों `y^(2) = x-1` और `x^2 =y-1` के मध्य की न्यूनतम दूरी है
05:43View Solutionसमाकलन `int_(-1/2)^(1/2)[[x]+ln((1+x)/(1-x))]dx` बराबर है
07:24View Solutionशब्द MONDAY के अक्षरों से बनाये जाने वाले अर्थ एवं बिना अर्थ के कितने शब्द बनाये जा सकते है, जबकि कोई अक्षर की पुनरावृत्ति नहीं हो, यदि
सभी अक्षरों का एक बार प्रयोग किया जाये02:25View Solutionयदि f(x + y,x - y) = xy, तब f(x, y) है
02:00View Solutionx तथा y के मान जो समीकरण `((1+i)x-2i)/(3+i)+((2-3i)y+i)/(3-i)=i` को संतुष्ट करते हैं होंगं:
08:49View Solutionएक वक्र की स्पर्श रेखा y-अक्ष को एक बिंदु P पर प्रतिच्छेद करती है। P से गुजरने वाली इस स्पर्श रेखा के लंबवत एक रेखा बिंदु (1,0) से गुजरती है। वक्र का अवकल समीकरण है:
View Solutionयदि m एक धनात्मक पूर्णांक है तथा `triangle_(r )=|(2r-1,(m) c_(r ),1),(m^(2)-1,2^(m),m+1),(sin^(2)(m^(2)),sin^(2)(m),sin^(2)(m+1))|` तब `underset(r=0)overset(m)Sigma triangle_(r )` का मान है
05:49View Solutionयदि `alpha=sin^(-1)((sqrt3)/2)+sin^(-1)(1/3)` और `beta=cos^(-1)((sqrt3)/2)+cos^(-1)(1/3)` तो,
04:43View Solution`phArrq` का तार्किक समतुल्य है
04:48View Solutionयदि `log_(10)((x^(3)-y^(3))/(x^(3)+y^(3)))=2` है, तब `(dy)/(dx)=`
04:15View Solutionयदि A,8 से छोटी सम प्राकृत संख्याओं का समुच्चय है और B.7 से छोटी अभाज्य संख्याओं का समुच्चय है, तब A से B में संबंधों की संख्या है
01:59View Solutionवास्तविक x के लिए, फलन `((x-a)(x-b))/((x-c))` के सभी वास्तिक मानों के लिए निम्न में से परिभाषित है
06:57View SolutionOPQR एक वर्ग है और M, N क्रमशः भुजाओं PQ और QR के मध्य बिंदु हैं, तब वर्ग और त्रिभुज OMN के क्षेत्रफलों का अनुपात है:
06:55View Solution`int(sin^(4)x)/(cos^(8)x)dx` बराबर है (जहां C एक स्वेच्छ अचर है)
04:02View Solutionयदि x = 3 वृत `x^2 + y^2 = 81` की स्पर्श जीवा है, तो इसके सापेक्ष स्पर्श रेखा युग्म का समीकरण है
02:59View Solutionअन्तराल `[0,2pi]` में `sin^(4) x + cos^(4) x = sin x . cos x` के हलों की संख्या है
04:36View Solutionएक मीनार, मीनार के पाद से गुजरने वाली एक क्षैतिज रेखा पर स्थित बिंदुओं A, B और C पर क्रमश: `alpha, 2alpha` और `3alpha` कोण बनाती है। यदि `(AB)/(BC) = 1+pcos(palpha)` है, तब p का मान है
08:15View Solutionमाना `y=sin^(-1)(sin 8) - tan^(-1)(tan 10) + cos^(-1)(cos 12) -sec^(-1)(sec 9)+`
` cot^(-1) (cot 6) - "cosec"^(-1) ("cosec"7)` यदि y सरल होकर `api + b` बनता है,
तो (a - b) का मान ज्ञात कीजिये।06:00View Solutionयदि `alpha ` और `beta` भिन्न सम्मिश्र संख्याएँ हैं जहाँ `|beta|=1`, तब `|(beta-alpha)/(1-bar(alpha)beta)|` का मान ज्ञात कीजिए ।
05:00View Solution`f(0)` का मान इस प्रकार है कि फलन `f(x)=(1-cos(1-cosx))/(x^(4))` प्रत्येक जगह सतत है तब f(0) का मान है
04:02View Solution
गणित questions and complete solutions for chapter JEE MAIN TEST-3 of NTA MOCK TESTS of Class 12
