Complete Solutions to MATHEMATICS of chapter JEE MOCK TEST 6 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | JEE MOCK TEST 6 |
| NTA MOCK TEST | MATHEMATICS |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
`sin alphax+cos alphax " and " abs(cosx)+abs(sinx)` are periodic functions of same fundamental period, if `alpha` equals
View SolutionDifferential coefficient of `log_10 x` w.r.t `log_x 10 ` is
View SolutionIf A,B and C are the angles of a triangle and
`|{:(1,1,1),(1+sinA,1+sinB,1+sinC),(sinA+sin^(2)A,sinB+sin^(2)B,sinCsin^(2)C):}|` =0
then `Delta` ABC must be .
View SolutionThe contrapositive of the statement ''If two triangles are identical, then they are similar'' is
View SolutionIf `f(x)=a-(x-3)^(8//9)`, then the maximum value of `f(x)` is
View SolutionWrite the value of `sin(cot^(-1)x)` .
View SolutionThe area bounded by the curves `y=x^2 and y=2/((1+x^2)` is
View SolutionEvaluate: `("Lim")_(x->0)(x^(6000)-(sinx)^(6000))/(x^2(sinx)^(6000))`
View SolutionIf [x] stands for the greatest integer function, the value of `overset(10)underset(4)int([x^(2)])/([x^(2)-28x+196]+[x^(2)])dx`, is
View SolutionThe shaded region in the give figure represents
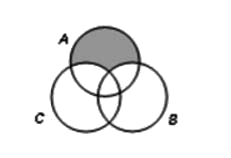 .
.
View SolutionIf `asin^2x+bcos^2x=c,bsin^2y+acos^2y=d` and `atanx=btany` then `a^2/b^2=........ (0ltx,yltpi/ 2)`
View SolutionNumber of points from where perpendicular tangents can be drawn to the curve `x^2/16-y^2/25=1` is
View SolutionThe sum of the first 20 terms common between the series 3 +7+11+15+... and 1+6+11 +16+... is
View SolutionLet 10 vertical poles standing at equal distances on a straight line , subtend the same angle of elevation `alpha` at a point O on this line and all the poles are on the same side of O. If the height of the longest pole is h and the distance of foot the smallest pole form O is `alpha` then the distance between two consecutive poles, is
View SolutionLet `vecu,vecv and vecw` be vectors such that `vecu+ vecv + vecw =0` if `|vecu|= 3, |vecv|=4 and |vecw|=5` then `vecu.vecv + vecv .vecw + vecw .vecu ` is
View SolutionThe total number of ways in which 5 balls of different colours can be distributed among 3 persons so that each person gets at least one ball is
View SolutionThe order of the differential equation whose general solution is given by `y=(C_1+C_2)cos(x+C_3)-C_4e^(x+C_5),` where `C_1,C_2,C_3,C_4,C_5` , are arbitrary constants, is
View SolutionIn a competitive examination, an examinee either guesses or copies or knows the answer to multiple choice question with four choices. The probability that he makes a guess is `1/3` and the probability that he copies the answer is 1/6. The probability that the answer is correct, given that he copies it, is `1/8`. Find the probability that he knows the answer to the question, given that he correctly answered
View SolutionThe number of values of `theta in [(-3pi)/(2), (4pi)/(3)]` which satisfies the system of equations.
`2 sin^(2) theta + sin ^(2) 2 theta = 2 and `
` sin 2 theta + cos 2 theta = tan theta ` is
View SolutionIf the three distinct lines
` x + 2ay + a = 0 , x+ 3by + b = 0` and
`x + 4ay + a = 0 ` are concurrent , then the point (a,b) lies on a .
View SolutionIf the line y - 2 =0 is the directrix of the parabola `x^(2) - ky + 32 =0, k ne 0` and the parabola intersects the circle `x^(2) + y^(2) = 8` at two real distinct points, then the absolute value of k is .
View SolutionIf `z_1, z_2 , z_3` are complex numbers such that `|z_1| = |z_2| = |z_3| = | 1/z_1 + 1/ z_2 + 1/ z_3| = 1,` Then find the value of `|z_1 + z_2 + z_3|` is :
View SolutionIf the `4^(th)` term of `{sqrt(x^((1)/(1+log_(10)x)))+root(12)(x)}^(6)` is equal to `200`, `x gt 1`and the logarithm is common logarithm, then `x` is not divisible by
View SolutionIf `int (dx)/(sqrt(x)+root(3)x)=asqrt(x) + b(root(3)x)+c(root(6)x)+d` In being an arbitary constant then the value of `20a + b+ c+d ` is
View SolutionGiven `f(x)={(x^2 xx e^(2(x-1)), 0 le x le 1), (a" "sgn(x+1)cos(2x-2)+bx^2, 1 lt x le2):}` is differentiable at `x=1`, then the value of `|a - b|` is
View Solution
MATHEMATICS questions and complete solutions for chapter JEE MOCK TEST 6 of NTA MOCK TESTS of Class 12