Complete Solutions to गणित of chapter JEE-MAIN TEST-25 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | JEE-MAIN TEST-25 |
| NTA MOCK TESTS | गणित |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
यदि `y=(1+x)^(y)+sin^(-1)(sin^(2)x)` है, तो `x=0` पर `(dy)/(dx)` है:
View Solution`f(x)=sin^(2)x` तथा `x-`अक्ष द्वारा `x=a` से `x=b` तक परिबद्ध क्षेत्रफल, जहाँ `f''(a)=f''(b)=0(AA a,bin(0,pi))` है:
View Solutionफलन `f(x)-(1)/(9-x^(2))+log_(20)(x^(3)-3x)` का प्रांत है :
View Solutionयदि 10 माप के एक नमूने के लिए, `sum_(i=1)^(10)(x_(i)-5)^(2)=350` और `sum_(i=1)^(10)(x_(i)-6)=20` है, तो प्रसरण है:
View Solutionयदि वास्तविक संख्यायें a तथा b,0 तथा 1 के मध्य इस प्रकार है कि बिंदु `z_(1)=a+i,z_(2)=1+bi` तथा `z_(3)=0` समबाहं त्रिभुज बनाते है तो a तथा b बराबर होंगे
View Solutionयदि दीर्घवृत्त `25x^(2)+9y^(2)=225` की कोई स्पर्श रेखा निर्देशांक अक्षो को A और B पर इस प्रकार मिलती है कि OA=OB तो, लम्बाई AB बराबर है (जहाँ, O मूल बिंदु है):
View Solutionयदि `(1)/(1!11!)+(1)/(3!9!)+(1)/(5!7!)=(2^(n))/(m!)` है, तो `m+n` का मान है :
View Solutionयहाँ दस सीट है जिनमे से चार अधिकृत है | इन चार सीटो पर चार व्यक्तियों को व्यवस्थित करने के तरीको की अंख्या, ताकि प्रत्येक व्यक्ति ठीक 1 पडोसी रखता है, है :
View Solutionमान लीजिए वक्र `y=f(x)`, समीकरण `(dy)/(dx)=1-(1)/(x^(2))` को संतुष्ट करता है और बिंदु `(2,(7)/(2))` से होकर गुजरता है, तो `f(1)` का मान है :
View Solutionयदि एक फलन `f:RtoR` को `f(x)=int(x^(8)+4)/(x^(4)-2x^(2)+2)dx` और `f(0)=1` के रूप में परिभाषित किया जाता है, तो निम्नलिखित में से कौन सा सही है ?
View Solutionछ: निष्पक्षपाती पासो को फेंका जाता है | शीर्ष फलको पर प्रकट होने वाली संख्याओ का गुणनफल अभाज्य होने कि प्रायिकता होगी :
View Solutionयदि x असमिका `(tan^(-1)x)^(2)+3(tan^(-1)x)-4gt0` को संतुष्ट करता है, तो x के मानो का पूर्ण समुच्चय है :
View Solutionमान लीजिए `2a+2b+c=0` हो, तो सरल रेखा `ax+by+c=0` का समीकरण, जो बिंदु (1,1) से सबसे अधिक दूर है, है:
View Solutionयदि x, `|x+1|` और `|x-1|` एक समांतर श्रेणी (A.P) के प्रथम तीन पद है, तो इसके 20 पदों तक इसका योगफल है :
View Solutionव्यंजक `3-cosx+sin^(2)x` के अधिकतम और न्यूनतम संभावित मान के लिए बीच का अंतर है :
View Solution`int_(0)^(12pi)([sint]+[-sint])dt` का मान बराबर है: (जहाँ, `[.]` महत्तम पूर्णांक फलन को दर्शाता है)
View Solutionफलन `f(x)=sinx+2cosx,vvx in[0,2pi]` के लिए, हम प्राप्त करते है :
View Solution`2x-y+z-3=0,3x+y+z=5` द्वारा निर्मित रेखा को रखने वाले और बिंदु `(2,1,-1)` से `(1)/(sqrt6)` इकाई पर स्थित एक समतल का समीकरण है :
View Solutionयदि `vecm_(a),vecm_(b)` और `vecm_(e),3` इकाई सदिश इस प्रकार है कि `vecm_(a)*vecm_(b)=0,vecm_(a)*vecm_(c)=0` और `vecm_(b)` और `vecm_(c)` के बीच का कोण `pi/3` है, तो `|vecm_(a)xxvecm_(b)-vecm_(a)xxvecm_(c)|` का मान बराबर है :
View Solutionमान लीजिए बिंदु A, `3x-4y+1=0` पर स्थित है, बिंदु B, `4x+3y-7=0` पर स्थित है और बिंदु C, `(-2,5)` है | यदि ABCD एक समचतुर्भुज है, तो D का बिंदुपथ है :
View Solutionमान लीजिए `A+2B=[[2,4,0],[6,-3,3],[-5,3,5]]` और `2A-B=[[6,-2,4],[6,1,5],[6,3,4]]` है, तो `tr(A)-tr(B)` बराबर है (जहाँ, `tr(A)=`आव्यूह A का ट्रेस अर्थात आव्यूह A के मुख्य विकर्ण अवयवो का योगफल)
View Solutionयदि `px^(4)+qx^(3)+rx^(2)+sx+f=`
`|(x^(2)+3x,x-1,x+3),(x+1,2-x,x-4),(x-3,x+4,3x)|` तो
दर्शाइए कि `f=18`.
View Solutionयदि `S=sum_(r=1)^(80)(r)/((r^(4)+r^(2)+1))` है, तो `(6481S)/(1000)` का मान है:
View Solutionयदि परवलय, जिसका अक्ष x-अक्ष है, के बिंदु `P(3,4)` पर स्पर्श रेखा का समीकरण, `3x-4y+7=0` है, तो परवलय की नाभि से स्पर्श की दुरी है :
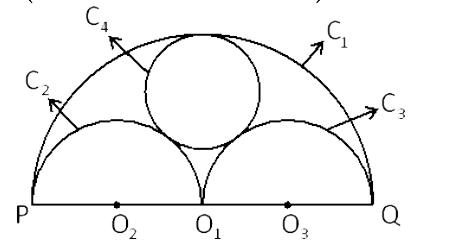
View Solutionआकृति में PQ, `PO_(1)` और `O_(1)Q` आर्धवृतो `C_(1),C_(2)` और `C_(3)` के व्यास है, जिनके केंद्र क्रमश: `O_(1),O_(2)` और `O_(3)` पर है और वृत्त `C_(4)`, अर्धवृतो `C_(1),C_(2)` और `C_(3)` को स्पर्श करता है | यदि `PQ=24` इकाई और वृत्त `C_(4)` का क्षेत्रफल A वर्ग इकाई है, तो `(8pi)/(A)` का मान बराबर है (यहाँ, `PO_(1)=O_(1)Q`):
View Solution
गणित questions and complete solutions for chapter JEE-MAIN TEST-25 of NTA MOCK TESTS of Class 12