Complete Solutions to MATHEMATICS of chapter NTA JEE MOCK TEST 25 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | NTA JEE MOCK TEST 25 |
| NTA MOCK TEST | MATHEMATICS |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
If `y=(1+x)^y+sin^-1(sin^2x)` , then `(dy)/(dx)` at x = 0 is
05:33View SolutionThe area bounded by `f(x)=sin^2x` and the x - axis from x = a to x = b , where `f''(a)=f''(b)=0(AAa,b,in(0,pi))` is
07:45View SolutionThe domain of the function `f(x)=1/(9-x^2)+log_(20)(x^3-3x)` is
04:35View SolutionIf for a sample size of `10`, `sum_(i=1)^(10)(x_i-5)^2=350 and sum_(i=1)^(10)(x_i-6)=20` , then the variance is
07:34View SolutionIf a and b are two real number lying between 0 and 1 such that `z_1=a+i, z_2=1+bi and z_3=0` form an equilateral triangle , then
05:32View SolutionIf any tangent to the ellipse `25x^(2)+9y^2=225` meets the coordinate axes at A and B such that OA = OB then , the length AB is equal to (where , O is the origin)
05:52View SolutionIf `1/(1!11!)+1/(3!9!)+1/(5!7!)=(2^n)/(m!)` then the value of m + n is
08:45View SolutionThere are 10 seats in the first row of a theatre of which 4 are to be occupied. The number of ways of arranging 4 persons so that no two persons sit side by side is:
03:56View SolutionLet the curve y = f (x) satisfies the equation `(dy)/(dx)=1-1/x^2` and passes through the point `(2,7/2)` then the value of f(1) is
01:20View SolutionIf a function `F: RrarrR` is defined as `f(x)=int(x^8+4)/(x^4-2x^2+2)dx` f (0) =1 , then which of the following is correct ?
03:07View SolutionSix fair dice are rolled . The probability that the product of the numbers appearing on top faces is prime is
03:43View SolutionIf x satisfies the inequality `(tan^-1x)^2+3(tan^-1x)-4gt0` , then the complete set of values of x is
05:06View SolutionLet `2a+2b+c=0` , then the equation of the straight line ax + by + c = 0 which is farthest the point (1,1) is
03:00View SolutionIf `x,|x+a|,|x-1|` are first three terms of an A.P., then the sum of its first 20 terms is
04:36View SolutionThe difference between the greatest and the least possible value of the expression `3-cosx +sin^2x` is
04:40View SolutionThe value of `int_0^(12pi) ([sint]+[-sint])dt` is equal to (where [.] denotes the greatest integer function )
07:43View SolutionFor the function `f(x)=sinx+2cosx,AA"x"in[0,2pi]` we obtain
04:25View SolutionFind the equation of the plane containing the lines 2x-y+z-3=0,3x+y+z=5 and at a distance of `1/sqrt6` from the point (2,1,-1).
08:31View SolutionIf `vecm_a,vecm_band vecm_c` are 3 units vectors such that `vecm_a.vecm_b= vecm_a.vecm_c=0` and the angle between `vecm_b.vecm_c " is " pi/3,` then then value of `|vecm_axxvecm_b -vecm_axxvecm_c |` is equal to
04:12View SolutionLet the points A lies on `3x-4y+1=0`, the point B lines on `4 x + 3 y - 7 = 0` and the point C is (-2,5) . If ABCD is a rhombus , then the locus of D is
04:38View SolutionLet `A+2B=[{:(2,4,0),(6,-3,3),(-5,3,5):}] and 2A-B=[{:(6,-2,4),(6,1,5),(6,3,4):}]` , then tr (A) - tr (B) is equal to (where , tr (A) =n trace of matrix x A i.e. . Sum of the principle diagonal elements of matrix A)
04:56View SolutionLet `px^4+qx^3+rx^2+sx+t=|{:(x^2+3x,x-1,x+3),(x+1,-2,x-4),(x-3,x+4,3x):}|` be an identity where p,q,r,s and t are constants, then the value of s is equal to
10:03View SolutionIf `S=sum_(r=1)^(80)(r)/((r^4+r^2+1))` , then the value of `(6481s)/(1000)` is
07:29View SolutionIf the equation of the tangent at the point P(3,4) on the parabola whose axis is the x - axis is 3x - 4y + 7 = 0 ,then distance of the tangent from the focus of the parabola is
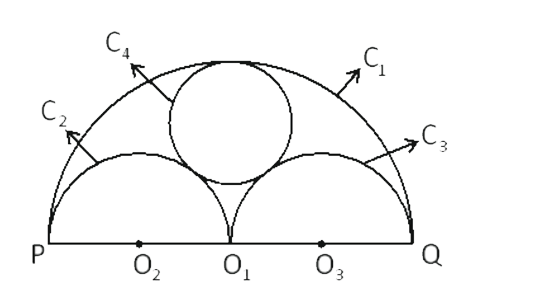
03:40View SolutionIn the figure PQ `PO_1 and O_1Q` are the diameters of semicircles `C_1,C_2 and C_3` with centres at `O_1 ,O_2 and O_3` respectively `C_1 C_2 and C_3` . If PQ = 24 units and the area of the circle `C_4` is A sq. units , then the value of `(8pi)/(4)` is equal ot (here, `PO_1 = O_1Q)`
 02:25View Solution
02:25View Solution
MATHEMATICS questions and complete solutions for chapter NTA JEE MOCK TEST 25 of NTA MOCK TESTS of Class 12
