Complete Solutions to गणित (एकल विकल्पी) of chapter JEE MAIN - 65 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | JEE MAIN - 65 |
| NTA MOCK TESTS | गणित (एकल विकल्पी) |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
`(1+x+x^(2)+x^(3))^(4)` के प्रसार में `x^(8)` का गुणांक है
View Solution7 असमान रिंग हैं। एक हाथ की चार अंगुलियों (अंगूठे को छोड़कर) पर पाँच रिंग को व्यवस्थित करने की संभव संख्या (प्रत्येक अंगुली पर रिंगों के क्रम की गणना की जानी है और यह आवश्यक नहीं है कि प्रत्येक अंगुली में एक रिंग है) बराबर है:
View Solutionयदि `tan^(2)(x+y) + cot^(2)(x+y) = 1-2x-x^(2)` है, तो (जहाँ, `n in Z`)
View Solutionदो समुच्चयों A और B के लिए, यदि n (A) = 7, n (B) = 13 और `n (A cap B) = 5` है, तब गलत कथन है
View Solution`lim_(x to (pi)/(2))([(x)/(3)])/(ln(sinx))` का मान है: (जहां, [.] महत्तम पूर्णांक फलन को दर्शाता है)
View Solutionमाना, g(x) = xf(x), जहाँ `f(x)={(x^(2)"sin"(1)/(x),:x ne 0),(0,:x=0):}` है। x = 0 पर,
View Solutionकथन "यदि `9 gt 10` तो `3^(2)=5`" का तुल्य कथन होगा:
View Solutionमाना A, समतल `x - 2y + 2z + 6 = 0` पर मूल बिंदु से डाले गये लंब का पाद है और B (0, – 1, – 4) समतल पर एक बिंदु है। तो, AB की लंबाई है:
View Solutionमाना एक समतल में तीन असंरेख सदिश , `veca, vecb` और `vecc` इस प्रकार हैं कि `|veca|=2, |vecb|=5` और `|vecc| =sqrt(29)` है। यदि `veca` और `vecc` के बीच का कोण `theta_(1)` है और `vecb` और `vecc` के बीच का कोण `theta_(2)` है, जहां `theta_(1), theta_(2) in [(pi)/(2), pi]` है, तो `theta_(1)+theta_(2)` का मान बराबर है:
View Solutionयदि समीकरणों का निकाय `2x-3y +5z =12, 3x +y+pz=q` और `x-7y+8z =17` संगत है, तब निम्न में से कौन सा सत्य नहीं है?
View Solutionयदि A एक सममित आव्यूह है और B एक विषम सममित आव्यूह है, तो निम्न में से कौन सा सही है?
View Solutionदिखाई गई आकृति में, OABC एक आयत है जहाँ OA = 3 इकाई, OC = 4 इकाई है। यदि BD = 2.5 इकाई है, तब विकर्ण OB की प्रवणता बराबर है
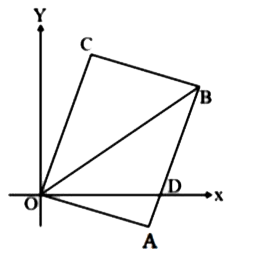
View Solutionरेखा `2x-y+1=0` वृत्त के बिन्दु (2, 5) पर स्पर्श रेखा है तथा वृत्त का केन्द्र रेखा `x+y=9` पर है। वृत्त का समीकरण निकाले।
View Solutionबिंदु (x, y) का बिंदुपथ, जिसकी रेखा y = 2x + 2 से दूरी (2,0) से दूरी के बराबर है, एक परवलय है जिसकी नाभिलम्ब जीवा की लंबाई परवलय `y = Kx^(2)` के समान है, तो K का मान बराबर है
View Solutionमाना `alpha` और `beta , x^(2)+x+1=0` के मूल हैं, तो वह समीकरण, जिसके मूल `alpha^(2020)` और `beta^(2020)` हैं, है:
View Solutionमाना समाकल `I= int((2020)^(x+sin^(-1)(2020)^(x)))/(sqrt(1-(2020)^(2x)))dx = K^(2)(2020)^(sin^(-1)(2020)^(x)) +lambda` (जहां, `lambda` समाकलन नियतांक है), तब `2020^(K)` का मान है:
View Solutionसमाकल `I= int_((pi)/(4))^((pi)/(2)) sin^(6) x dx` संतुष्ट करता है
View Solutionअवकल समीकरण `(dy)/(dx) =2y tan x +tan^(2)x, AA x in (0, (pi)/(2))` का व्यापक हल `yf (x) =(x)/(2)-(sin(2x))/(4) +C` (जहां, C एक स्वेच्छ अचर है) है। यदि `f((pi)/(4))=(1)/(2)` है, तो `f((pi)/(3))` का का मान बराबर है:
View Solutionयदि दीर्घवृत्त `(x^(2))/(25) +(y^(2))/(9) =1` के लघु अक्ष पर दो बिंदुओं को केंद्र से नाभियों के समान दूरी पर लिया जाता है, तो दीर्घवृत्त की किसी भी स्पर्शरेखा पर इन बिंदुओं से लंबवत दूरियों के वर्गों का योग है:
View Solutionयदि (-3, -1) सबसे बड़ा अंतराल है जिसमें फलन `f(x) =x^(3) +6x^(2) +ax +2` ह्रासमान है, तब [a] बराबर है: (जहां, [.] महत्तम पूर्णांक फलन को दर्शाता है)
View Solution
गणित (एकल विकल्पी) questions and complete solutions for chapter JEE MAIN - 65 of NTA MOCK TESTS of Class 12