Complete Solutions to गणित of chapter JEE MAIN TEST 71 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | JEE MAIN TEST 71 |
| NTA MOCK TESTS | गणित |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
समीकरण `sqrt(x + 14 - 8sqrt(x -2)) + sqrt(x + 23 - 10sqrt(x - 2)) = 3`के वास्तविक हलों की संख्या हैं
View Solutionयदि संख्याएँ `3^(2a - 1) , 14, 3^(4 - 2a) (0 lt a lt 1)` समांतर श्रेढ़ी के प्रथम तीन पद हैं, तब इसका पाँचवाँ पद बराबर है
View Solutionयदि `y = "sin"^(-1) (2x)/(1+x^(2))` हो, तो `(dy)/(dx)` ज्ञात कीजिए ।
View Solutionफलन `f (x) = log_3 [1 – log_6 (x^2 – 7x + 16)] `का प्रांत है
View Solution`lim_(x to - oo)(x^2 tan(2/x))/(sqrt(16x^2 - x + 1))` का मान बराबर है
View Solutionसंयुक्त कथन `(p to ~q) vv (p ^^ q)` से निम्न के तुल्य है
View Solutionमीनार CD का इसके दक्षिण की ओर स्थित बिंदु A पर उन्नयन कोण `60^@` है और A के पश्चिम की ओर स्थित बिंदु B पर उन्नयन कोण `30^@` है। यदि AB = 5 किमी है, तब मीनार की ऊंचाई है: (जहाँ, C, B और A एक ही धरातल पर है)
View Solutionयदि `x = sin (2 tan^(-1)2sqrt(3))` और `y = sin (1/2 tan^(-1) (12/5))` है, तब
View Solutionवक्र `f (x) = x/(1 - x^2)` पर बिंदु, जहां इसकी स्पर्शरेखा की ढाल इकाई के बराबर है, `(x_1,y_1), (x_2, y_2)` और `(x_3, y_3)` हैं, तो `x_1 + x_2 + x_3` बराबर है
View Solutionनिम्नलिखित कथनों में से कौनसा सही है?
View Solutionवक्रों `y = e^x cos x` और `y = e^x sin x` के बीच `x = pi/4` से `x = pi/2` तक परिबद्ध क्षेत्रफल (वर्ग इकाई में) है
View Solutionबिंदु `P (2,7/2)` से होकर गुजरने वाला और बिंदु `P (x, y)` पर `1 - 1/(x^2)` ढाल वाला वक्र निम्न बिंदु से भी गुजरता है
View Solutionएक थैले में 2 लाल, 3 सफ़ेद और 5 काली गेंदें हैं, एक गेंद को निकाला जाता है जिसका रंग लिखा जाता है और उसे प्रतिस्थापित कर दिया जाता है। यदि n परीक्षण में पहली बार लाल गेंद प्राप्त होने की कम से कम प्रायिकता `2/25` है, तब n का सबसे बड़ा मान बराबर है
View Solutionयदि a, b, c शून्येतर वास्तविक संख्याएं हैं, तब समीकरणों की निकाय
`y+z = a+2x, x +z = b+2y`,
`x+ y = c+ 2z `संगत है और `b = 4a + c/4`, तब समीकरण `at^2 + bt + c = 0` के मूलों का योगफल है
View Solutionमाना A कोटि 3 का आव्यूह इस प्रकार है कि `A^2 = 3A – 2I ` जहां, I कोटि 3 का एक तत्समक आव्यूह है। यदि `A^5 = alpha A + beta I` है, तब `alpha beta` बराबर है
View Solutionएक रेखा L समतल `2x - y – z = 4` में इस प्रकार स्थित है कि यह रेखा `(x - 2)/2 = (y - 3)/1 = (z - 4)/5`के लंबवत है। रेखा L दी गई रेखा और दिए गए समतल के प्रतिच्छेद बिंदु से गुजरती है। निम्नलिखित में से कौन सा बिंदु रेखा L को संतुष्ट करता है?
View Solutionएक रेखा `4x + y = 1` बिंदु A (2, -7) से होकर गुजरती है और रेखा BC को B पर मिलती है जिसका समीकरण `3x - 4y + 1 = 0` है। यदि रेखा AC का समीकरण जबकि `AB = AC ` है, `x/a + y/b = 1` है, तब a का मान बराबर है
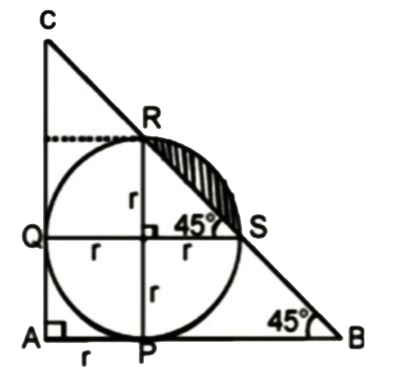
View SolutionABC एक समकोण त्रिभुज है, जो शीर्ष A पर समकोण है। एक वृत्त खींचा जाता है जो भुजा AB और AC को क्रमश: P और Q पर स्पर्श करता है जबकि P और Q से गुजरने वाले व्यासों के अन्य सिरे भुजा BC पर स्थित है। यदि AB = 6 इकाई है, तब त्रिभुज के बाहर स्थित वृत्तखंड का क्षेत्रफल (वर्ग इकाई में) है
View Solutionयदि `e_1` और `e_2` क्रमश: दीर्घवृत्त `(x^2)/(18) + (y^2)/4 = 1` और अतिपरवलय `(x^2)/9 - (y^2)/4 = 1` की उत्केन्द्रता हैं और `(e_1, e_2)` दीर्घवृत्त `15x^2 +3y^2 = k` पर एक बिंदु है, तब k का मान बराबर है
View Solutionदो बिंदु P और Q आर्गंड समतल में सम्मिश्र संख्याओं z और `3z + 2 + i` को निरूपित करते हैं। यदि `|z|= 2` हैं, तब Q वृत्त पर गतिमान है, जिसका केंद्र और त्रिज्या हैं
(यहाँ, `i^2 = -1`)
View Solutionमाना AB एक परवलय की नाभीय जीवा है और D और C क्रमश: A और B से इसकी नियता पर डाले गये लंबों के पाद हैं। यदि CD = 6 इकाई है और चतुर्भुज ABCD का क्षेत्रफल 36 वर्ग इकाई है, तब जीवा AB की लम्बाई (इकाई में) है
View Solutionकुल 6 लड़कों और 6 लड़कियों को एकान्तर क्रम मे एक पंक्ति और एक वृत्त में बैठना है। माना m पंक्ति में व्यवस्थाओं की संख्या है और n वृत्त में व्यवस्थाओं की संख्या है। यदि `k = m/(10 n)` है, तब k का मान है:
View Solutionमाना `veca = hati + 2 hatj + 3hatk , vecb = hati - hatj + 2hatk`और `vecc = (x - 2)hati - (x - 3)hatj - hatk` है। यदि `vecc, veca` और `vecb` के समतल में स्थित है, तब `1/x` बराबर है
View Solutionयदि `I = int (dx)/(x^2.sqrt(1 + x^2)) = (f(x))/(x) + C, (AA x gt 0)` (जहां, C समाकलन नियतांक है) और `f(1) = - sqrt(2)` तब `| f (sqrt3)|` का मान है
View Solution`(sqrt(5) + root(8)(7))^(1024)`के प्रसार में पूर्णांक पदों की संख्या है
View Solution
गणित questions and complete solutions for chapter JEE MAIN TEST 71 of NTA MOCK TESTS of Class 12