Complete Solutions to गणित of chapter JEE MAIN TEST 72 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | JEE MAIN TEST 72 |
| NTA MOCK TESTS | गणित |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
रेखा `x =(c)/(2)` शीर्ष (0,0), (1,1) और (9,1) वाले त्रिभुज को दो क्षेत्रों में विभाजित करती है। यदि दोनों क्षेत्रों का क्षेत्रफल बराबर है, तब C बराबर है
View Solutiony-अक्ष की वृत्त के केंद्र से दूरी, जो प्रथम चतुर्थांश में स्थित है (आकृति देखें) और रेखाओं `y=(1)/(2)x,y=4` और x- अक्ष को स्पर्श करता है,
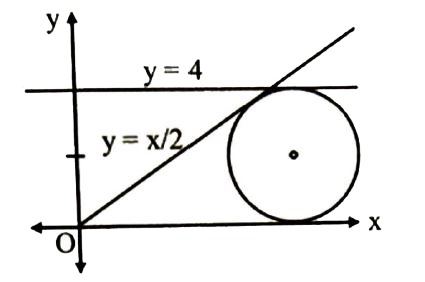
View Solutionपरवलय `y^(2)=8x` के बिंदु P (2,4) पर एक स्पर्शरेखा खींची जाती है जो x-अक्ष को Q पर प्रतिच्छेद करती है, इससे एक अन्य स्पर्शरेखा परवलय पर खींची जाती है जो इसे R पर स्पर्श करती है। यदि R पर अभिलंब परवलय को पुनः S पर प्रतिच्छेद करता है, तब S के निर्देशांक हैं
View Solutionदीर्घवृत्त `3x^(2) +4y^(2) = 12` की नाभिलंब जीवा के सिरों पर खींची गई स्पर्शरेखाएं एक समचतुर्भुज PQRS बनाती हैं। दीर्घवृत्त के बाहर समचतुर्भुज PQRS का क्षेत्रफल (वर्ग इकाई में) बराबर है
View Solutionफलन `f(x)=min{|x^(2)-4|,|x^(2)-1|}` पर विचार कीजिए, तब उन बिंदुओं की संख्या जहाँ f (x) अन-अवकलनीय है, है/ हैं
View Solutionयदि `f: A to Bf(x)=2sinx-2cosx+3 sqrt(2)` के रूप में परिभाषित एक प्रतिलोम फलन है, तो सही कथन हो सकता है
View Solution32 छात्रों की एक कक्षा का औसत भार 40 किग्रा है। यदि शिक्षक का भार शामिल किया जाता है, तब औसत भार में `(1)/(3)` किग्रा की वृद्धि होती है, तो शिक्षक का भार है
View Solutionएक प्रेक्षक को पता चलता है कि मीनार का उन्नयन कोण `theta` है। मीनार की ओर 3 मीटर आगे बढ़ने पर उन्नयन कोण `45^(@)` है, और मीनार की ओर 2 मीटर ओर आगे बढ़ाने पर उन्नयन कोण `90^(@) -theta` है। मीनार की ऊंचाई है (मान लें कि प्रेक्षक की ऊंचाई नगण्य है और प्रेक्षक मीनार के पाद के समान स्तर पर स्थित है)
View Solutionमाना `veca=2hati-hatj+3hatk,vecb=hati+hatj4hatk` और शून्येतर सदिश : इस प्रकार है कि `(vecaxx vecb)xx vec c=vecaxx( vecbxx vecc)` है तो सदिश `vecc` हो सकता है
View Solutionमाना a, b और c समीकरण `x^(3)-7x^(2)+9x-13=0` के मूल हैं और A और B,A `=[{:(a,b,c),(b,c,a),(c,a,b):}]` और
`B=[{:(bc-a^(2),ca-b^(2),ab-c^(2)),(ca-b^(2),ab-c^(2),bc-a^(2)),(ab-c^(2),bc-a^(2),ca-b^(2)):}]` दिए गए दो आव्यूह हैं, तब |A||B का मान बराबर हैं
View Solutionएक समतल `P_(1)` का समीकरण `4x-2y+2z=3` है और `P_(2)` का समीकरण `-x + ky-2z = 7` है। यदि `P_(1)` और `P_(2)` के बीच का कोण `(2pi)/3` है, तब k का मान हो सकता है
View Solutionमाना `A=[(0,i),(i,0):}]` जहाँ `i^(2)=-1` है। माना I कोटि 2 के तत्समक आव्यूह को दर्शाता है, तो `I+A+A^(2)+A^(3)......A^(110)` बराबर है
View Solutionकिस मान से अधिक सभी n के लिए असमिका `""^(n+1)C_(6)+""^(n)C_(4) gt ""^(n+2)C_(5)-""^(n)C_(5)` सत्य है?
View Solutionयदि समीकरण `x^(2) – mx +1 = 0` के दोनों मूल इकाई से छोटे हैं, तब
View Solutionअंतराल `[0,2pi]` में समीकरण `sin^(3)x cosx+sin^(2) cos^(2)x+cos^(3)x sin x=1` के हलों की संख्या बराबर है
View Solutionअवकल समीकरण `(dy)/(dx)+(xy)/(1-x^(2))=xsqrt(y),(|x| lt1)` का हल
`sqrt(y)=-(f(x))/(3)+C(1-x^(2))^((1)/(4))` है, जहां `f((1)/(2))=(3)/(4)` और C एक स्वेच्छ अचर है। तब, `f(-(1)/(2))` का मान है
View Solutionसिमा `L=lim_(n to oo) sum_(r=1)^(n) (n)/(n^(2)+r^(2))` संतुष्ट करती है
View Solutionयदि समाकल `I= int (x^(5))/( sqrt(1+x^(3)))dx=K sqrt(x^(3)+1)(x^(3)-2)+C` (जहां, C समाकलन नियतांक है), तब 9K का मान बराबर है
View Solutionr = a पर फलन `f(x)=2x^(3)-3(a+b)x^(2)+6abx` का एक स्थानीय उच्चिष्ठ है, यदि
View Solutionयदि `A={x:x=3^(n)-2n-1,n in N}` और `B={x:x=4(n-1), n in N}` है, तब
View Solutionयदि वक्रों `x^(2)+y^(2) le 4, x+y le2` और `y ge1` द्वारा परिबद्ध क्षेत्रफल `(2pi)/(K)-(sqrt(K))/(2)-(1)/(2)` वर्ग इकाई है, तब K का मान बराबर है
View Solutionएक अनंत गुणोत्तर श्रेढ़ी का दूसरा पद 2 है और इसके अनंत पदों का योगफल 8 है। पहला पद है
View Solutionएक बम के सेतु को भेदने की प्रायिकता `(2)/(3)` है। सेतु को नष्ट करने के लिए दो सीधे भेदन की आवश्यकता है। अभीष्ट बमों की न्यूनतम संख्या जबकि सेतु के नष्ट होने की प्रायिकता `(3)/(4)` से अधिक है, है:
View Solution`lim_(x to 0)(9 ln(2-cos 25x))/(ln^(2)(sin3x+1))` का मान बराबर है
View Solutionविभिन्न सम्मिश्र संख्याओं z की संख्या, जबकि `|z| = 1` और `z^(3)` पूर्णत: काल्पनिक है, निम्न के बराबर है। हैं:
View Solution
गणित questions and complete solutions for chapter JEE MAIN TEST 72 of NTA MOCK TESTS of Class 12