Complete Solutions to गणित of chapter JEE MAIN TEST 91 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | JEE MAIN TEST 91 |
| NTA MOCK TESTS | गणित |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
यदि `x,y` और : z समीकरण `2t^3-(tan[x+y+z]pi)t^2-111t+2020=0` के मूल हैं, तब `|(x,y,z),(y,z,x),(z,x,y)|` बराबर है: (जहां, [x],x से कम या बराबर महत्तम पूर्णांक मान को दर्शाता है)
View Solutionमाना सभी `"x"in= [–2, 2]` के लिए, `f(x)=min{sqrt(4-x^2),sqrt(1+x^2)}` है, तब बिंदुओं की संख्या, जहाँ `f (x)` अन-अवकलनीय है, है:
View Solutionएक समस्या को 3 छात्रों द्वारा स्वतंत्र रूप से हल करने की प्रायिकता क्रमश: `1/2,1/3` और a है। यदि समस्या के हल होने की प्रायिकता P(S) है, तब P(S) निम्न अंतराल में स्थित है (जहाँ, `ain(0,1))`
View Solutionएक आव्यूह `A=[(0,1,2),(0,-3,0),(1,1,1)]` पर विचार कीजिए। यदि`6A^(-1)=aA^2+bA+cI` जहाँ `a,b,cinZ` और I एक तत्समक आव्यूह है, तब a + 2b+3c बराबर है:
View Solutionयदि `29(""^(30)C_0) +28(""^(30)C_1)+27(""^(30)C_2)+.......+ 1(""^(30)C_(28))+0.(""^(30)C_(29))-(""^(30)C_(30))` के योगफल का मान `K. 2^(32)` के बराबर है, तब K का मान बराबर है:
View Solutionसमाकल `I=intunderset(1/sqrt(3))oversetsqrt(3)""(dx)/(1+x^2+x^3+x^5)` का मान बराबर है.
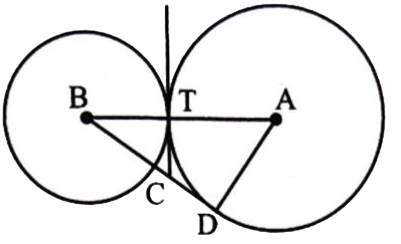
View SolutionA और B पर केंद्रित दो वृत्त एक दूसरे को T पर बाह्य स्पर्श करते हैं। माना BD, D पर स्पर्शरेखा है और TC एक उभयनिष्ठ स्पर्शरेखा है। यदि AT की लम्बाई 3 इकाई है और BT की लम्बाई 2 इकाई है, तब CB की लम्बाई (इकाई में) हैं
View Solutionमाना `a_n = 16, 4, 1,` ...... एक गुणोत्तर श्रेढ़ी है। `sum_(n=1)^(oo)rootn(P_n)` का मान, जहाँ `P_n` प्रथम n पदों का गुणनफल है, बराबर है:
View Solutionप्रथम चतुर्थांश में वक्र इस प्रकार है कि OP की प्रवणता वक्र के बिंदु P पर खींची गई स्पर्शरेखा की दोगुनी है, जहाँ O मूलबिंदु है और P वक्र पर कोई व्यापक बिंदु है। यदि वक्र (4, 2) से होकर गुजरता है, तब इसका समीकरण है:
View Solutionस्कूल के प्रत्येक कार्य दिवस में छह कालांश होते हैं। उन तरीकों की संख्या, जिसमें 5 विषयों को इस प्रकार व्यवस्थित किया जा सकता है कि प्रत्येक विषय के लिए कम से कम एक कालांश आवंटित किया जाए और कोई कालांश खाली ना रहे, है:
View Solutionयदि `y^2=4x` और रेखा `y = mx(AAm""in[1,3])` द्वारा परिबद्ध अधिकतम क्षेत्रफल k वर्ग इकाई है, तब 3k से बड़ी सबसे छोटी अभाज्य संख्या है:
View Solutionअनिश्चित समाकलन `inte^(e^x)((xe^(x).lnx+1)/x)dx` का सरलतम रूप निम्न है: (जहाँ, c समाकलन नियतांक है)
View Solutionबिंदुओं `(m, –9)` और `(7,m)` से होकर गुजरने वाली रेखा की प्रवणता m है। तब, इस रेखा का x- अंतःखंड है:
View Solutionc के पूर्णांक मानों की संख्या, जिसके लिए समीकरण `x^2-2cx+c^2=1` के दोनों मूल, ` -2` से अधिक परन्तु 4 से कम हैं, है
View Solutionअतिपरवलय `x^2/(25)-y^2/36=1` की जीवाओं के मध्य बिंदु का बिंदुपथ जो (2, 4) से होकर गुजरता है, एक अतिपरवलय है, जिसके अनुप्रस्थ अक्ष की लम्बाई (इकाई में) बराबर है:
View Solutionसम्मिश्र संख्या z का वास्तविक भाग, जो `|z-1-2i|le1` को संतुष्ट करता है और न्यूनतम धनात्मक कोणांक रखता है, है:
View Solution10 प्रेक्षणों के माध्य और प्रसरण क्रमश:10 और 5 पाए जाते हैं। पुनः जाँच करने पर पाया जाता है कि प्रेक्षण 5 गलत है। यदि गलत प्रेक्षण को 15 से बदल दिया जाता है, तब सही प्रसरण है:
View Solution`lim_(x to pi)(tan (picos^(2)x))/(sin^(2)x)` का मान बराबर है
View Solutionयदि `f (x) = (x ^(2) - [ x ^(2) ] )/( 1 + x ^(2) - [ x ^(2) ] ) ` (जहाँ [.], के महत्तम पूर्णांक भाग को दर्शाता है), तो f (r) का परिसर है
View Solutionयदि समतल `x-3y+2z=1` और रेखा `(x-1)/2=(y-1)/(-1)=(z-1)/(-3)` के बीच का कोण `theta` है, तब `sec2theta` बराबर है:
View Solutionयदि `veca, vecb` और `vecc` तीन सदिश इस प्रकार हैं कि `3veca+4vecb+6vecc=vec0,|veca|=3,|vecb|=3` और `|vecc|=4` है, तब `-864((veca.vecb+vecb.vecc.+vecc.veca)/6)` का मान बराबर
View Solutionयदि समीकरण `(7picosx)=cot(7pisinx)` के मुख्य हलों की संख्या k है, तब `k/5` बराबर है:
View Solutionx के वास्तविक मानों की संख्या जो समीकरण `x^4+4x^3+12x^4+7x-3=0` को संतुष्ट करती है, है:
View Solutionयदि परवलय `y^2=4x` की नाभिलम्ब जीवा के अंतिम सिरों पर खींचे गये अभिलम्ब, वृत्त `(x-3)^2+(y+2)^2=r^2` की स्पर्शरेखाएँ हैं, तब `r^4` का मान बराबर है:
View Solutionएक व्यक्ति एकसमान चाल से एक सीधे पथ पर एक ऊर्ध्वाधर खंभे की ओर चल रहा है। पथ पर एक निश्चित बिंदु A पर, वह देखता है कि खंभे के शीर्ष का उन्नयन कोण `30^@` है। A से `5(sqrt(3)+1)` मिनट उसी दिशा में चलने के बाद, एक बिंदु B पर, वह देखता है कि खंभे के शीर्ष का उन्नयन कोण `45^@` है, तब उसके द्वारा B से खंभे तक पहुंचने के लिए लिया गया समय (मिनट में) है:
View Solution
गणित questions and complete solutions for chapter JEE MAIN TEST 91 of NTA MOCK TESTS of Class 12