Complete Solutions to MATHEMATICS of chapter NTA JEE MOCK TEST 91 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | NTA JEE MOCK TEST 91 |
| NTA MOCK TEST | MATHEMATICS |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
If x, y and z are the roots of the equation `2t^(3)-(tan[x+y+z]pi)t^(2)-11t+2020=0`, then `|(x,y,z),(y,z,x),(z,x,y)|` is equal to (where, `[x]` denotes the greatest integral value less than or equal to x)
03:13View SolutionLet `f(x)="min"{sqrt(4-x^(2)),sqrt(1+x^(2))}AA,x in [-2, 2]` then the number of points where `f(x)` is non - differentiable is
04:03View SolutionThe probability of a problem being solved by 3 students independently are `(1)/(2), (1)/(3)` and `alpha` respectively. If the probability that the problem is solved in P(S), then P(S) lies in the interval (where, `alpha in (0, 1)`)
03:53View SolutionConsider a matrix `A=[(0,1,2),(0,-3,0),(1,1,1)].` If `6A^(-1)=aA^(2)+bA+cI`, where `a, b, c in and I` is an identity matrix, then `a+2b+3c` is equal to
03:30View SolutionIf the value of the sum `29(.^(30)C_(0))+28(.^(30)C_(1))+27(.^(30)C_(2))+…….+1(.^(30)C_(28))+0.(.^(30)C_(29))-(.^(30)C_(30))` is equal to `K.2^(32)`, then the value of K is equal to
04:37View SolutionThe value of the integral `I=int_((1)/(sqrt3))^(sqrt3)(dx)/(1+x^(2)+x^(3)+x^(5))` is equal to
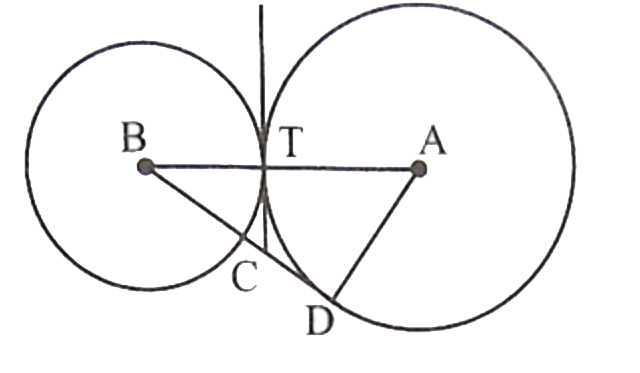
04:37View SolutionTwo circles with centres at A and B touch each other externally at T. Let BD is the tangent at D and TC is a common tangent. If AT has length 3 units and BT has length 2 units, then the length (in units ) of CB is
 03:31View Solution
03:31View SolutionLet `a_(n)=16,4,1,………..` be a geometric sequence. The value of `Sigma_(n=1)^(oo)rootn(P_(n))`, where `P_(n)` is the product of the first n terms, is equal to.
03:06View SolutionA curve in the first quadrant is such that the slope of OP is twice the slope of the tangent drawn at P to the curve, where O is the origin and P is any general point on the curve. If the curve passes through (4, 2), then its equation is
03:40View SolutionThere are six periods in each working day of the school. In how many ways can one arrange 5 subjects such that each subject is allowed at least one period?
04:47View SolutionIf the maximum area bounded by `y^(2)=4x` and the line `y=mx(AA m in [1, 3])` is k square units, then the smallest prime number greater than 3k is
04:30View SolutionThe indefinite integral `inte^(e^(x))((xe^(x).lnx+1)/(x))dx` simplifies to (where, c is the constant of integration)
02:56View SolutionThe line through the points `(m, -9)` and `(7, m)` has slope m. Then, the x - intercept of this line is
03:47View SolutionAll the values of m for which both roots of the equation `x^2-2mx +m^2-1=0` are greater than -2 but less than 4, lie in the interval
03:07View SolutionThe locus of the midpoint of the chords of the hyperbola `(x^(2))/(25)-(y^(2))/(36)=1` which passes through the point (2, 4) is a hyperbola, whose transverse axis length (in units) is equal to
06:31View SolutionThe real part of the complex number z satisfying `|z-1-2i|le1` and having the least positive argument, is
06:40View SolutionThe mean and variance of 10 observations are found to be 10 and 5 respectively. On rechecking it is found that an observation 5 is incorrect. If the incorrect observation is replaced by 15, then the correct variance is
05:05View SolutionThe value of `lim_(xrarrpi)(tan(picos^(2)x))/(sin^(2)(2x))` is equal to
04:13View SolutionIf `f(x)=(x^(2)-[x^(2)])/(x^(2)-[x^(2)-2])` (where, `[.]` represents the greatest integer part of x), then the range of f(x) is
08:21View SolutionIf the angle between the plane `x-3y+2z=1` and the line `(x-1)/(2)=(y-1)/(-1)=(z-1)/(-3)` is `theta`, then `sec 2 theta` is equal to
07:02View SolutionIf `veca, vecb and vecc` are three vectors such that `3veca+4vecb+6vecc=vec0, |veca|=3, |vecb|=3 and |vecc|=4`, then the value of `-864((veca.vecb+vecb.vecc+vecc.veca)/(6))` is equal to
07:15View SolutionIf the number of principal solutions of the equation `tan(7pi cos x)=cot(7pi sin x)` is k, then `(k)/(5)` is equal to
06:34View SolutionThe numberof real values of x that satisfies the equation `x^(4)+4x^(3)+12x^(2)+7x-3=0` is
04:55View SolutionIf the normals of the parabola `y^(2)=4x` drawn at the end points of its latus rectum are tangents to the circle `(x-3)^(2)+(y+2)^(2)=r^(2)`, then the value of `r^(4)` is equal to
07:36View SolutionA man is walking towards a vertical pillar in a straight path at a uniform speed. At a certain point A on the path, he observes that the angle of elevationof the top of the pillar is `30^(@)`. After walking for `5(sqrt3+1)` minutes from A in the same direction, at a point B, he observes that the angle of elevation of the top of the pillar is `45^(@)`. Then the time taken (in minutes) by him, to reach from B to the pillar, is (take `sqrt3=1.73`)
08:36View Solution
MATHEMATICS questions and complete solutions for chapter NTA JEE MOCK TEST 91 of NTA MOCK TESTS of Class 12
