Complete Solutions to PHYSICS of chapter NTA JEE MOCK TEST 42 of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | NTA JEE MOCK TEST 42 |
| NTA MOCK TEST | PHYSICS |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
A satellite in a force-free space sweeps stationary interplantary dust at a rate `(dM)/(dt) = beta upsilon`, where `upsilon` is the speed of escaping dust w.r.t. satellite and `M` is the mass of satellite at that instant. The acceleration of satellite is
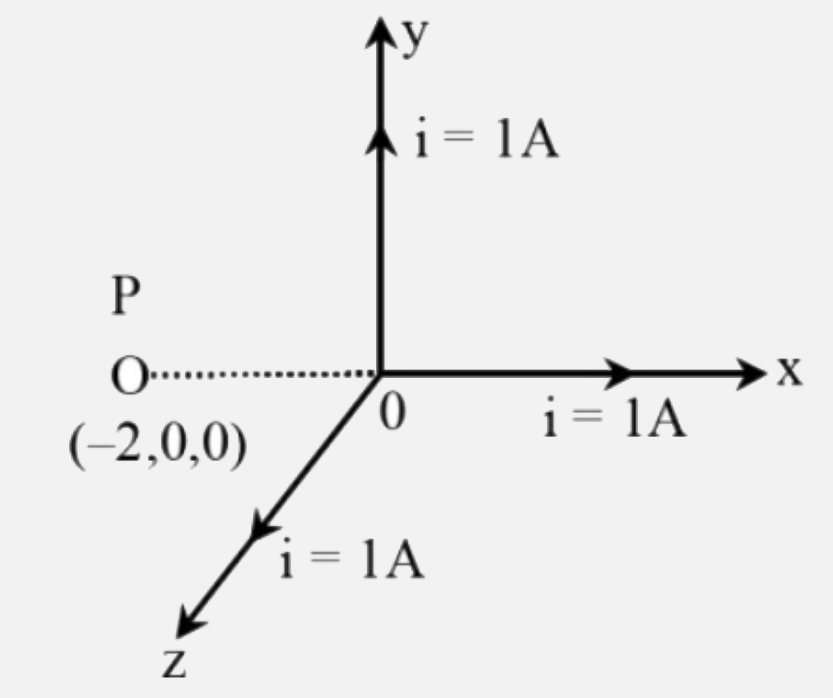
View SolutionThree semi - inifinte wires, each carrying a current of 1 A are placed on each of the coordinate axes with their ends at the origin, as shown in the figure. The magnetic induction at point `P(-2m, 0,0)` is
View SolutionA heating element has a resistance of 100 `Omega` at room temperature. When it is connected to a supply of 220 V, a steady current of 2A passes in it and temperature is `500^(@)C` more than room temperature. What is the temperature coefficient of resistance of the heating element ?
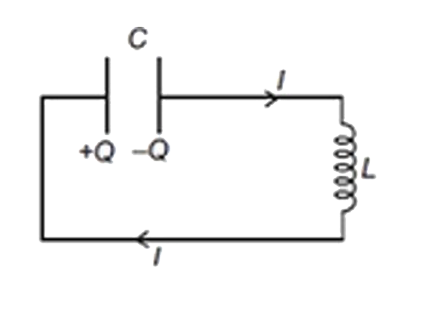
View SolutionIn the LC circuit shown below, the current is in direction as shown and the charges on the capacitor plates have the sign as shown. At this instant
View SolutionA non - conducting disc of radius R is uniformly charged with surface charge density `sigma`. A disc of radius `(R )/(2)` is cut from the disc, as shown in the figure. The electric potential at centre C of large disc will be

View SolutionA stationary object is released from a point P a distance 3R from the centre of the moon which has radius R and mass M. which one of the following expressions gives the speed of the object on hitting the moon?
View SolutionA point source of heat of power P is placed at the centre of a thin spherical shell of a mean radius R. The material of the shell has thermal conductivity K. Calculate the thickness of the shell if the temperature difference between the outer and inner surfaces of the shell in steady - state is T.
View SolutionA vertical closed cylinder is separated into two parts by a frictionless piston of mass m and of negligible thickness. The piston is free to move along the length of the cylinder. The length of the cylinder above the piston is `l_(1)`, and that below the piston is `l_(2)`, such that `l_(1)gtl_(2)`. Each part of the cylinder contains n moles of an ideal gas at equal temeprature T. If the pistion is stationary, its mass, m, will be given by : (R is universal gas constant and g is the acceleration due to gravitey)
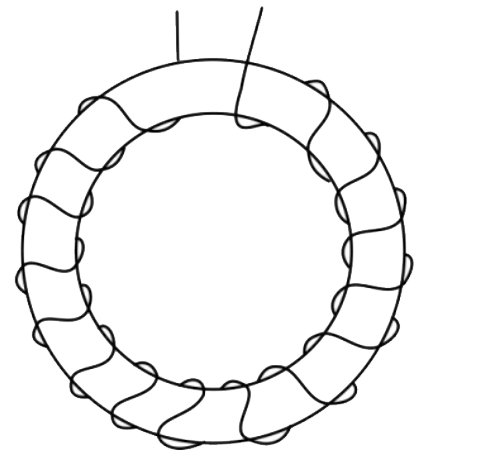
View SolutionConsider a toroid of circular cross - section of radius b, major radius R much greater than minor radius b, (see diagram) find the total energy stored in magnetic field of toroid -
View SolutionA convex lens forms an image of an object on a screen. The height of the image is 9 cm . The lens is now displaced until an image is again obtained on the screen. Then height of this image is 4 cm . The distance between the object and the screen is 90 cm.
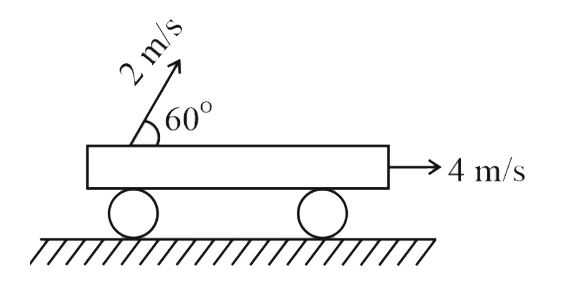
View SolutionA ball is projected with a speed of `2ms^(-1)` with respect to a trolley which is moving with `4ms^(-1)`, as shown in the figure. The angle at which ball is projected with respect to the horizontal in ground frame is
View SolutionA cube of mass m is placed on top of a wedge of mass 2m, as shown in figure. There is no friction between the cube and the wedge. The minimum co - efficient of friction between the wedge and the horizontal surface, so that the wedge does not move is
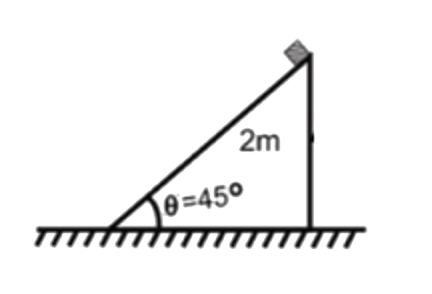
View SolutionThe radius of germanium `(Ge)` nuclide is measured to be twice the radius of `._(4)^(9)Be`. The number of nucleons in `Ge` are
View SolutionThe rediation emitted when an electron jumps from `n = 3 to n = 2` orbit in a hydrogen atom falls on a metal to produce photoelectron. The electron from the metal surface with maximum kinetic energy are made to move perpendicular to a magnetic field of `(1//320) T` in a radius of `10^(-3) m`. Find (a) the kinetic energy of the electrons, (b) Work function of the metal , and (c) wavelength of radiation.
View SolutionA biconvex lens of focal length `f_(1)=10cm` is placed 40 cm in front of a concave mirror of focal length `f_(2)=7.50 cm,` as shown in the figure. An object, 2 cm high, is placed 20 cm to the left of the lens.

The image formed by the lens, as rays travel to the right, is
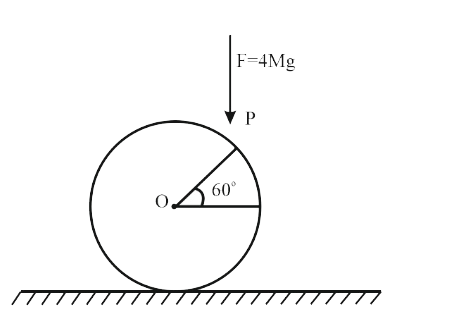
View SolutionA uniform solid sphere of mass M and radius R is lying on a rough horizonal plane. A constant force `F=4Mg` acts vertically downwards at point P such that the line OP makes an angle of `60^(@)` with the horizontal as shown in the figure. The minimum value of the coefficient of friction `mu` so that sphere performs pure rolling, is
View SolutionA black body at 200 K is found to emit maximum energy at a wavelength of `14mu m`. When its temperature is raised to 1000 K, the wavelength at which maximum energy is emitted is
View SolutionA sperical body of mass `m` and radius `r` is allowed to fall in a medium of viscosity `eta`. The time in which the velocity of the body increases from zero to `0.63 ` times the terminal velocity `(v)` is called constant `(tau)`. Dimensionally , `tau` can be represented by
View SolutionTwo slits `S_(1)` and `S_(2)` illuminated by a white light source give a white central maxima. A transparent sheet of refractive index 1.25 and thickness `t_(1)` is placed in front of `S_(1)`. Another transparent sheet of refractive index 1.50 and thickness `t_(2)` is placed in front of `S_(2)`. If central maxima is not effected, then ratio of the thickness of the two sheets will be :
View SolutionWhen a train approaches a stationary observer, the apparent frequency of the whistle is `n'` and when the same train recedes away from the observer, the apparent frequency is `n"`. Then the apperent frquency `n` when the observer sitting in the train is :
View SolutionSeparation energy of a hydrogen like ion from its third excited state is 2.25 times the separation energy of hydrogen atom from its first excited state. Find out the atomic number of this hydrogen like ion.
View SolutionA small sphere is given vertical velocity of magnitude `v_0=5ms^-1` and it swings in a vertical plane about the end of a massless string. The angle `theta` with the vertical at which string will break, knowing that it can withstand a maximum tension equal to twice the weight of the sphere, is
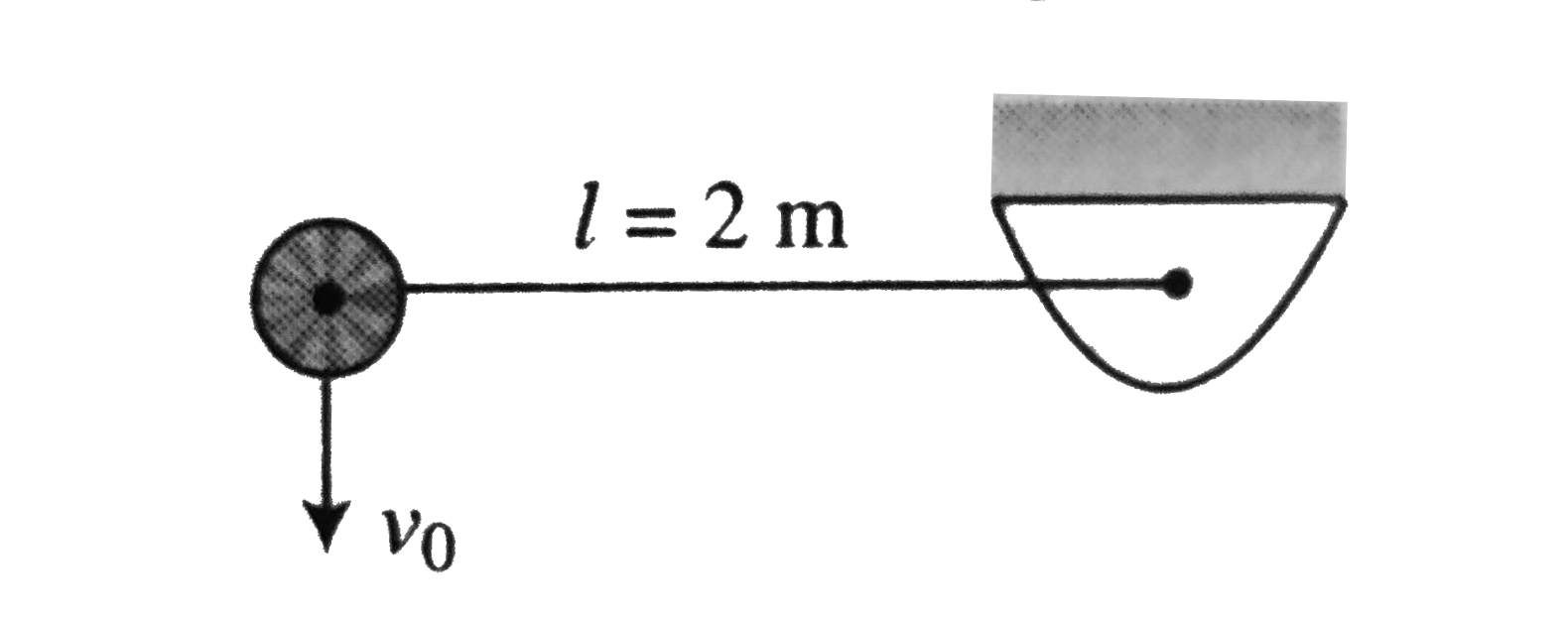
View SolutionFigure shows a particle mass `m = 100g` attaches with four identical spring , each of length `l = 10 cm` . Initial tension in each spring is `F_(0) = 25 N`. Neglecting gravity , Calculate the period of small oscillation of the particle along a line perpendicular to the plane of the figure .

View SolutionConsider three rods of length `L_(1), L_(2) and L_(3)` espectively joined in series. Each has same cross - sectional area with Young's moduli Y, 2Y and 3Y respectively and thermal coefficients of linear expansion `alpha, 2alpha and 3alpha` respectively. They are placed between two rigid fixed walls. The temperature of the whole system is increased and it is found that length of the middle rod does not change with temperature rise. Find the value of `(9L_(1))/(L_(3))`.
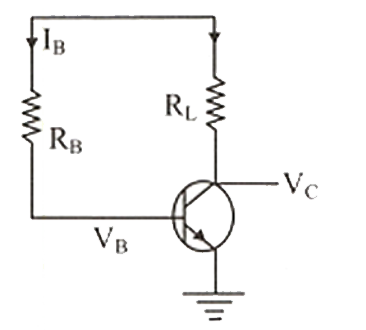
View SolutionIn the circuit of CE amplifier, a silicon transistor is used. The value of `V_("CC")=+20V, R_(L)=3kOmega`, collector voltage `=5v, beta=100`. Then the base resistance `R_(B)` should be `……xx10^(5)Omega`
(Take input voltage drop across Si transistor = 0.7 V)
View Solution
PHYSICS questions and complete solutions for chapter NTA JEE MOCK TEST 42 of NTA MOCK TESTS of Class 12