Complete Solutions to PHYSICS of chapter NTA JEE MOCK TEST 85 of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | NTA JEE MOCK TEST 85 |
| NTA MOCK TEST | PHYSICS |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
Derive an expression for the magnetic field at the site of the nucleus in a hydrogen atom due to the circular motion of the electron Assume that the atom is in its ground state and the answer in terms of fundamental constants
View SolutionParticles of masses m, 2m, 3m ... nm gram are placed on the same line at distance 1, 21, 31, ..., nl cm from a fixed point. The distance of centre of mass of the particles from the fixed point in cm is
View Solution`AB` is a light rigid rod. Which is rotating about a vertical axis passing through `A,A` spring of force constant `K` and natural length `l` is attached at `A` and its other end is attached to a small bead of mass `m`. The bead can slide without friction on the rod. At the initial moment the bead is at rest (w.rt. the rod) and the spring is unstreached Select correct option
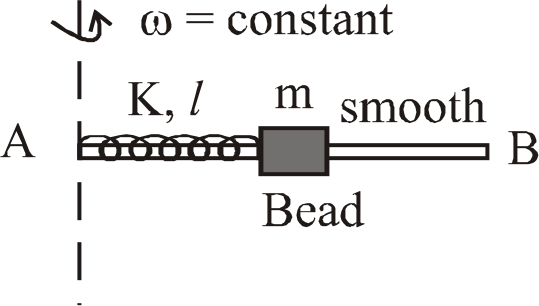
View SolutionIn the circuit shown in the figure (A), `R_(3)` is a variable resistance
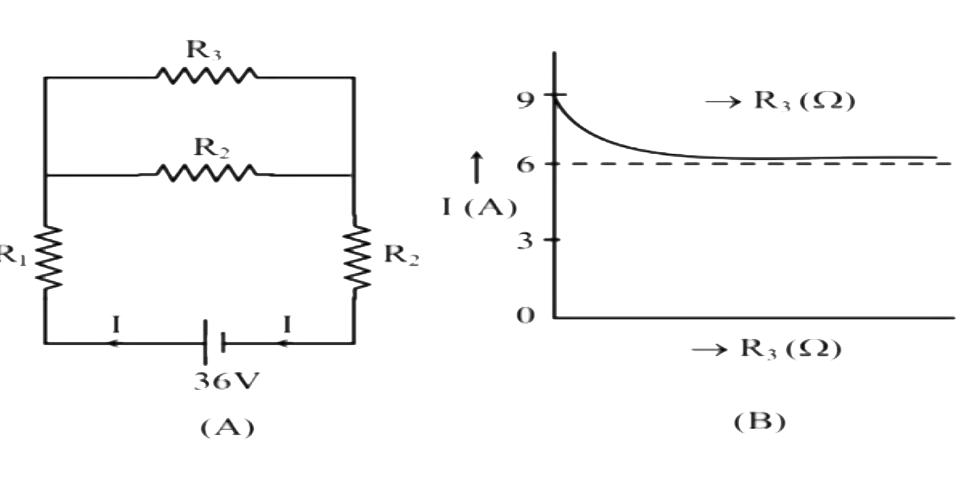
As the value `R_(3)` is changed, current I though the cell varies as shown. Obvioulsy, the variation is asymptotic, i.e. `Irarr6A` as `R_(3)rarroo`. Resistance `R_(1) and R_(2)` are, respectively
View SolutionIn a uniform magneitc field of induced B a wire in the form of a semicircle of radius r rotates about the diameter of hte circle with an angular frequency `omega`. The axis of rotation is perpendicular to hte field. If the total resistance of hte circuit is R, the mean power generated per period of rotation is
View SolutionAn insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density `rho=(A)/(r )`, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
View SolutionAssuming the Sun to be a spherical body of radius R at a temperature of TK, evaluate the total radiant powered incident of Earth at a distance r from the sun
where `r_0` is the radius of the Earth and `sigma` is Stefan's constant.
View SolutionIn a given process on an ideal gas, `dW=0 and dQlt0.` Then for the gas
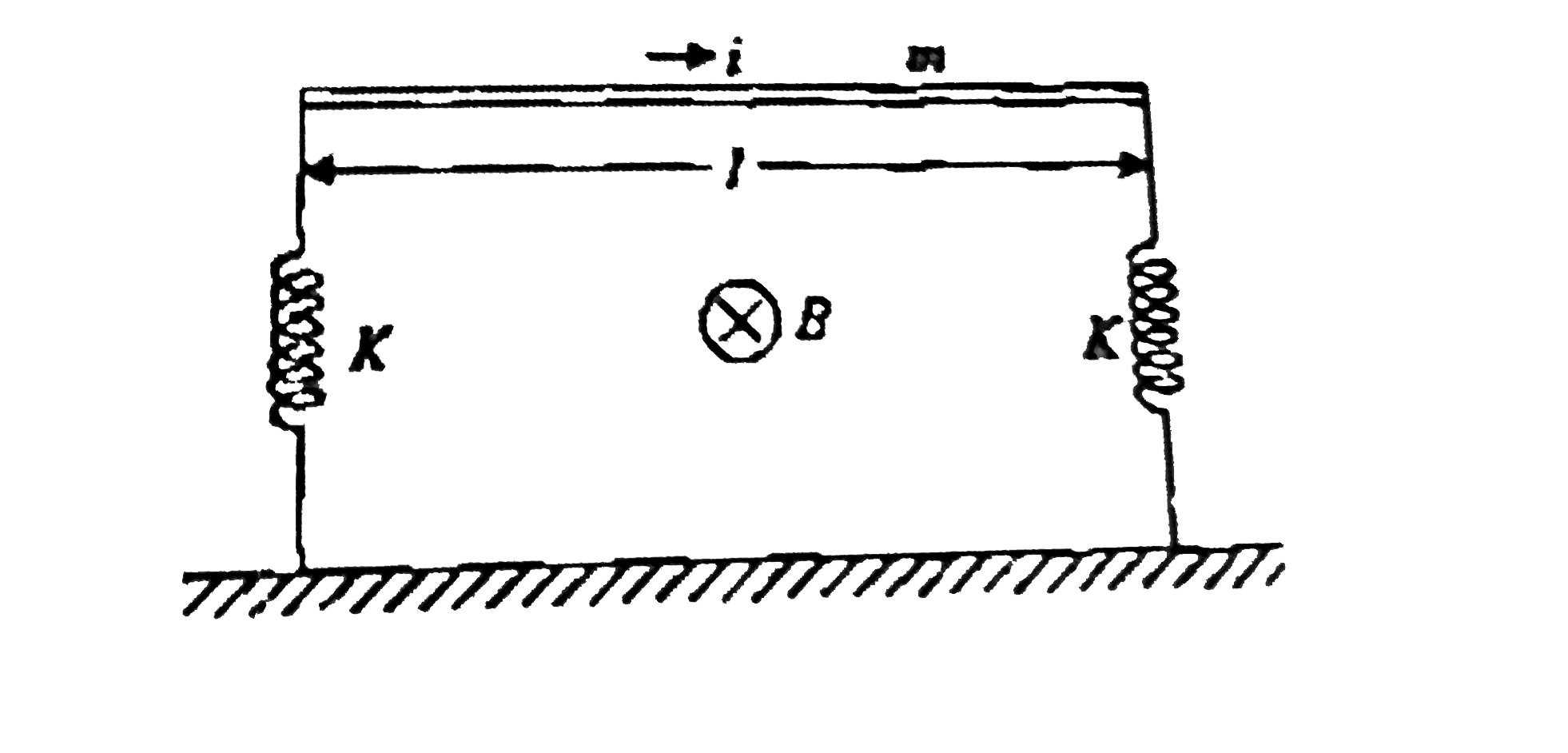
View SolutionA horizontal metallic rod of mass 'm' and length 'l' is supported by two vertical identical springs of spring constant 'k' each and natral length `l_(0)` A current 'l' is flowing in the rod in the direction shown if the rod is in equilibrium then the length of each spring in this state is:
View SolutionA large , heavy box is sliding without friction down a smooth plane of inclination `theta` . From a point `P` on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is `u` , and the direction of projection makes an angle `alpha` with the bottom as shown in Figure .
(a) Find the distance along the bottom of the box between the point of projection `p` and the point `Q` where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .

View SolutionThe friction coefficient between the board and the floor shown in figure is `mu` Find the maximum force that the man can exert on the rope so that the board does not slip on the floor

View SolutionA particle at the end of a spring executes simple harmonic motion with a period `t_(1)` while the corresponding period for another spring is `t_(2)` if the oscillation with the two springs in series is T then
View SolutionA photocell is illuminated by a small bright source places `1` m away when the same source of light is placed `(1)/(2)` m away. The number of electron emitted by photocathode would be
View SolutionA beam of light consisting of red, green and blue colours is incident on a right angled prism. The refractive index of the material of the prism for the above red, green and blue wavelengths are 1.39, 1.44 and 1.47, respectively.

View SolutionA uniform rod of mass m and length L is hinged at one end and free to rotate in the horizontal plane. All the surface are smooth. A particle of same mass m collides with the rod with a speed `V_(0)`. The coefficient of restitution for the collision is `e=(1)/(2)`. If hinge reaction during the collision is zero then the value of x is :

View SolutionA particular semiconductor in equilibrium has `1xx10^(16)cm^(-3)` donor atoms, `1.1xx10^(17)cm^(-3)` acceptor atoms. If the intrinsic carrier density `(n_(i))` of the semiconductor is `10^(12)cm^(-3)`, then the electron density in it will be
View SolutionThe speed `(v)` of ripples on the surface of waterdepends on surface tension `(sigma)`, density `(rho)` and wavelength `(lambda)`. The square of speed `(v)` is proportional to
View SolutionThe ratio of intensities of consecutive maxima in the diffraction pattern due to a single slit is
View SolutionA string of length 1.5 m with its two ends clamped is vibrating in fundamental mode. Amplitude at the centre of the string is 4 mm. Minimum distance between the two points having amplitude 2 mm is:
View SolutionThe potential energy of a `1 kg` particle free to move along the x- axis is given by `V(x) = ((x^(4))/(4) - x^(2)/(2)) J`
The total mechainical energy of the particle is `2 J` . Then , the maximum speed (in m//s) is
View SolutionThe length of a magnet is large compared to its width and breadth. The time period of its oscillation in a vibration magnetometer is 150 ms. The magnet is cut along its length into three equal parts and three parts are then placed on each other with their like poles toghether. The time period of this combination (in ms) will be
View SolutionA statellite is launched into a circular orbit, `(R )/(4)` above the surface of the earth. The time period of revolution is `T=2pi(n)^(3//2)sqrt((R )/(g))`. Where R is the radius of the earth and g is the acceleration due to gravity. Then what is the value on n?
View SolutionTo determine the half life of a radioactive element , a student plote a graph of in `|(dN(t))/(dt)| versus t , Here |(dN(t))/(dt)|` is the rate of radioatuion decay at time t , if the number of radoactive nuclei of this element decreases by a factor of p after `4.16 ` year the value of p is

View SolutionA wide cylindrical vessel `50cm` in height is filled with water and rests on a table. Assuming the viscosity to be negligible, find at what height from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance `l_(max)` from the vessel. Find `l_(max)`.
View SolutionA wire is made by attaching two segments together end to end. One segment is made of aluminium and the other is steel. The effective coefficient of linear expansion of the two segment wire is `19xx10^(-6)//^(@)C`. The fraction length of aluminium is (linear coefficient of thermal expansion of aluminium and steel are `23xx10^(-6).^(@)C` and `12xx10^(-6)//^(@)C`,
View Solution
PHYSICS questions and complete solutions for chapter NTA JEE MOCK TEST 85 of NTA MOCK TESTS of Class 12