Complete Solutions to Exercise of chapter CHEMICAL KINETICS of Class 12 book with complete answers and questions
| Class 12 | CHEMISTRY |
| Chapter | CHEMICAL KINETICS |
| P BAHADUR | Exercise |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Derive the relationship between rate of reaction, rate of disappearence of `X, Y` and rate of formation of `X_(2)Y_(3)` for the reaction:
`2X+3Yrarr X_(2)Y_(3)`
View Solution`2N_(2)O_(5) rarr 4NO_(2) + O_(2)`
If `(-d[N_(2)O_(5)])/(dt) = k_(1)[N_(2)O_(5)]`
`(d[NO_(2)])/(dt) = k_(2)[N_(2)O_(5)]`
`(d[O_(2)])/(dt) = k_(3)[N_(2)O_(5)]`
What is the relation between `k_(1), k_(2)`, and `k_(3)`?
View SolutionWhich of the following will react fastest (in terms of amount of product formed in a give time) and which will react at the highest rate?
(a) `1` mole of `A` and `1` mole of `B` in `1` litre vessel.
(b) `2` mole of `A` and `2` mole of `B` in `2` litre vessel.
(c ) `0.2` mole of `A` and `0.2` mole of `B` in `0.1` liter vessel.
View Solution`N_(2)O_(5)` decomposes according to equation,
`2N_(2)O_(5) rarr 4 NO_(2)+O_(2)`
(a) What does `-(d[N_(2)O_(5)])/(dt)` denote?
(b) What does `(d[O_(2)])/(dt)` denote?
(c) What is the unit of rate of this reaction?
View SolutionThe reaction, `2N_(2)O_(5)rarr 4NO_(2)+O_(2)`, shows an increase in concentration of `NO_(2)` by `20xx10^(-3)` mol `litre^(-1)` in `5` second. Calculate:
(a) rate of appearance of `NO_(2)`,
(b) rate of reaction and
(c ) rate dissappearance of `N_(2)O_(5)`.
View SolutionFor the decomposition reaction:
`N_(2)O_(4(g))rarr 2NO_(2(g))`, the initial pressure of `N_(2)O_(4)` falls from `0.46` atm to `0.28` atm in `30` minute. What is the rate of appearance of `NO_(2)`?
View SolutionThe rate of change in concentration of `C` in the reaction, `2A+Brarr 2C+3D`, was reported as `1.0` mol `litre^(-1) sec^(-1)`. Calculate the reaction rate as well as rate of change of concentration of A, B and D.
View SolutionThe decompoistion of `N_(2)O_(5)` in `C CI_(4)` solution at `318 K` has been studied by monitoring the concentration of `N_(2)O_(5)` in the solution. Initially, the concentration of `N_(2)O` is `2.33 M` and after `184 min`, it is reduced to `2.08 M`. The reaction takes place according to the equation:
`2N_(2)O_(5) rarr 4NO_(2) + O_(2)`
Calculate the average rate of this reaction in terms of hours, minutes, and seconds. What is the rate of Production of `NO_(2)` during this period?
View SolutionA chemical reaction `2A rarr 4B+C`, in gaseous phase shows an increase in concentration of `B` by `5xx10^(-3) M` in `10` second. Calculate:
(a) rate of appearance of `B`,
(b) rate of the reaction,
(c ) rate of disappearance of `A`.
View SolutionThe reaction, `2NO+Br_(2)rarr 2NOBr`, is supposed to follow the following mechanism,
(i) `NO+Br_(2) overset("fast")(hArr) NOBr_(2)`
(ii) `NOBr_(2) +NO overset(slow)(rarr)2NOBr`
suggest the rate law expression.
View SolutionThe thermal decomposition of `N_(2)O_(5)` occurs in the following steps:
Step I: `N_(2)O_(5) overset("slow")(rarr) NO_(2)+NO_(3)`
Step II: `N_(2)O_(5)+NO_(3)overset("fast")(rarr)3NO_(2)+O_(2)`
Overall reaction, `2N_(2)O_(5)rarr 4NO_(2)+O_(2)`
Suggest the rate expression.
View SolutionFor the reaction,
`4NH_(3(g))+5O_(2(g))rarr 4NO_((g))+6H_(2)O_((g))`, the rate of reaction in terms of disappearance of `NH_(3)` is `-(d[NH_(3)])/(dt)`, then write the rate expression in terms of concentration of `O_(2), NO` and `H_(2)O`.
View SolutionThe rate law expression for the reaction,
`2NO+O_(2) rarr 2NO_(2)` is: rate `=K[NO][O_(2)]`
Suggest the possible mechanism.
View SolutionIt has been proposed that the conversion of ozone into `O_(2)` proceeds in two steps:
`O_(3(g)) hArrO_(2(g))+O_((g))`
`O_(3(g))+O_((g))rarr 2O_(2(g))`
(a) Write the equation for overall reaction.
(b) Identify the intermediate, if any.
(c ) Derive molecularity for each step of mechanism.
View SolutionIn a reaction, `2Ararr` Products the concentration of A decreases from `0.5` "mol" litre^(-1)` to `0.4` "mol" litre^(-1)` in `10` minutes. Calculate rate during this interval.
View SolutionIn a reaction, `n_(1)A+n_(2)B rarr m_(1)C+m_(2)D, 5mol litre^(-1)` of `A` are followed to react with `3 mol litre^(-1)` of `B`. After `5` second, the concentration of `A` was found to be `B`. After `5` second, the concentration of `A` was found to be `4M`. Calculate rate of reaction in terms of `A` and `D`.
View SolutionFor the reaction, `2A + B+C rarr A_(2)B+C`
The rate `= k[A][B]^(2)` with `K = 2.0 xx 10^(-6) M^(-2) s^(-1)`. Calculate the initial rate of the reaction when `[A] = 0.1M, [B] = 0.2M` and `[C] = 0.8M`. IF the rate of reverse reaction is negligible then calculate the rate of reaction after `[A]` is reduced to `0.06M`.
View SolutionThe reaction `2A + B + C rarr D + 2E` is found to be first order in `A`, second order in `B` and zero order in `C`.
(a) Write the rate expresison.
(b) What is the effect on rate on increaisng the concentration of `A, B`, and `C` two times ?
View SolutionFor, `underset(("excess"))(2A) + B+C rarr` Products, calculate the:
(a) rate expression.
(b) units of rate and rate constant.
( c) effect on rate if concentration of `A` is doubled and of `B` is tripled.
View SolutionFind the order of reaction for the rate expression rate `= K[A][B]^(2//3)`. Also suugest the units of rate and rate constant for this expression.
View SolutionThe rate of decomposition of `NH_(3)` on platinum surface is zero order. What are rate of production of `N_(2)` and `H_(2)` if `k=2.5 xx 10^(-4)Ms^(-)`?
View SolutionAt `25^(@)C`, the rate constant for the reaction `I^(-) + ClO^(-) rarr IO^(-) + Cl^(-)` is `0.0606 "litre mol"^(-1) sec^(-1)`. If a solution is intially `1.0 M` in `I^(-)` and `5.0 xx 10^(-4) M` in `ClO^(-)`. Can you calculate the `[CO^(-)]` after `300 sec`? If yes, then how much ? If no, then why ?
View SolutionA reaction is second order with respect to a reaction. How is the rate of reaction affected if the
(a) doubled, (b) reduced to `1//2`?
View SolutionA reaction is first order in `A` secod order in `B`:
(i) write differential rate equation.
(ii) How is the rate affected when the concentration of `B` is tripled ?
(iii) How is the rate affected when the concentration of both `A` and `B` is doubled?
View SolutionThe decomposition of `N_(2)O_(5)` takes place according to `I` order as: `2N_(2)O_(5) rarr 4NO_(2)+O_(2)`
Calculate:
(a) The rate constant, if instantaneous rate is `1.4 xx 10^(-6) mol litre^(-1) sec^(-1)` when concentration of `N_(2)O_(5)` is `0.04M`.
(b) The rate of reaction when concentration of `N_(2)O_(5)` is `1.20 M`.
(c ) The concentration of `N_(2)O_(5)` when the rate of reaction will be `2.45 xx 10^(-5) mol litre^(-1) sec^(-1)`
View SolutionFor the decomposition,
`N_(2)O_(5)(g) rarr N_(2)O_(4)(g) + 1//2O_(2)(g)`, the initial pressure of `N_(2)O_(5)` is `114 mm` and after `20 sec`, the pressure of reaction mixture becomes `133 mm`.
Calculate the rate of reaction in terms of :
(a) change in pressure `sec^(-1)` and
(b) change in molarity `sec^(-1)`. Given that reaction is carried out at `127^(@)C`.
View SolutionThe decomposition of `N_(2)O_(5)` at an initial pressure of `380 mm` and `50^(@)C` is `50%` complete in `56` minutes and `71%` complete in `100` minutes. What is the order of reaction? How much of `N_(2)O_(5)` will decomposes in `100` minutes at `50^(@)C` but at an initial pressure of `500 mm`?
View SolutionIn a pseudo first order hydrolysis of ester in water the following result6s were obtained:
`{:(t//s,0,30,60,90),(["Ester"],0.55,0.31,0.17,0.085):}`
(i) Calculate the average rate of reaction between the time interval `30` to `60` seconds.
(ii) Calculate the pseudo first order rate constant for the hydrolysis of ester.
View SolutionCalculate the half life of a first order reaction from their rate constants given below `:`
`a. 200s^(-1)`,`b. 2 mi n^(-1)`,`c.4years^(-1)`
View SolutionThe rate constant for a first order reaction is `60s^(-1)`. How much time will it take to reduce the initial concentrationof the reactant to its `1//16th` value ?
View SolutionDuring nuclear explosion, one of the products is `.^(99)Sr` with half`-` life of `28.1 `years. If `1 mug` of `.^(90)Sr` was absorbed in the bones of a newly born baby instead of calcium, how much of its will remain after 10 years and 60 years if it is not lost metabolically.
View SolutionA substance reacts according to `I` order kinetics and rate constant for the reaction is `1 xx 10^(-2) sec^(-1)`. If its initial concentration is `1M`.
(a) What is initial rate?
(b) What is rate after `I` minute ?
View SolutionA first order reaction takes `69.3` minutes for `50%` completion. How much time will be needed for `80%` completion?
View SolutionShow that time required to complete `99.9%` completion of a first order reaction is `1.5` times to `99%` completion.
View SolutionThe thermal decomposition of compound is of first order. If `50%` of a sample of the compound is decomposition in `120 min` how long will it take for `90%` of the compound to decompose?
View SolutionA first order gas reaction has `k = 1.5 xx 10^(-6) s^(-1)` at `200^(@)C`. If the reaction is allowed to run for `10 h`, what have changed in the Product? What is the half-life of this reaction?
View SolutionThe rate constant for a first order reaction was found to be `0.082 min^(-1)`. If initial concentration of reactant is `0.15M`, how long would it take:
(a) to reduce the concentration of `A` to `0.03 M`?
(b) to reduce the concentration of A by `0.03 M`?
View SolutionFrom the rate expression for the following reactions, determine their order of reaction and dimensions of the rate constants.
`a. 3NO(g) rarr N_(2)O(g),` Rate`=k[NO]^(2)`
`b. H_(2)O_(2)(aq)+3I^(c-)(aq)+2H^(o+) rarr 2H_(2)O(l)+I_(3)^(c-),` Rate`=k[H_(2)O_(2)][I^(c-)]`
`c. CH_(3)CHO(g)rarr CH_(4)(g)+CO(g),` Rate`=k[CH_(3)CHO]^(3//2)`
`d. C_(2)H_(5)Cl(g) rarr C_(2)H_(4)(g)+HCl(g),` Rate `k[C_(2)H_(5)Cl]`
View SolutionFor a reaction, `3A rarr` Products, it is found that the rate of reaction becomes nine times if concentration of `A` is increased three times, calculate order of reaction.
View SolutionThe experiment data for the reaction `2A + B_(2) rarr 2AB` is
`|{:("Experiment",[A] M,[B_(2)] M,"Initial rate" (mol L^(-1) s^(-1)),),(I,0.50,0.5,1.6 xx 10^(-4),),(II,0.50,1.0,3.2 xx 10^(-4),),(III,1.00,1.0,3.2 xx 10^(-4),):}|`
Write the most probable rate equation for the reacting giving reason for you answer.
View SolutionIn a reaction between A and B, the initial rate of reaction was measured for different initial concentration of A and B as given below:
`{:(A//M,0.20,,0.20,0.40),(B//M,0.30,,0.10,0.05),(r_(0)//M s^(-1),5.07xx10^(-5),,5.07xx10^(-5),7.6xx10^(-5)):}`
View SolutionThe reaction between A and B is first order with respect to A and zero with respect to B. Fill in tha blanks in the following table:
`{:("Experiment",,[A]//M,[B]//M,"Initial rate"//"M min"),(I.,,0.1,0.1,2.0xx10^(-2)),(II.,,....,0.2,4.0xx10^(-2)),(II.,,0.4,0.4,.......),(IV.,,....,0.2,2.0xx10^(-2)):}`
View SolutionThe data given below are for the reaction of `NO` and `Cl_(2)` to from `NOCl` at `295 K`.
`{:([Cl_(2)],[NO],,,"Initial rate" (mol litre^(-1) sec^(-1))),(0.05,0.05,,,1xx10^(-3)),(0.15,0.05,,,3xx10^(-3)),(0.05,0.15,,,9xx10^(-3)):}`
(a) What is the order with respect to `NO` and `Cl_(2)` in the reaction?
(b) Write the rate expression.
(c ) Calculate the rate constant.
(d) Determine the reaction rate when conc. of `Cl_(2)` and `NO` are `0.2 M` and `0.4 M` respectively.
View SolutionCalculate the rate of reaction for the change, `2Ararr` Products, when rate constant of the reaction is `2.1xx10^(-5) time^(-1)` and `[A]_(0)=0.2M`.
View SolutionDerive order of reaction for the decomposition of `H_(2)O_(2)` from the following data.
`{:("Time (in minutes)",0,10,20,30),("Volume of" KMnO_(4),25,16,10.5,7.09):}`
needed for `H_(2)O_(2)`
View SolutionFor reaction `RX + OH^(-) rarr ROH + X^(-)`, rate expression is `R = 4.7 xx 10^(-5) [RX][OH^(-)] + 2.4 xx 10^(-5)[RX]`.
What `%` of reactant react by `S_(N)2` mechanism when `[OH^(-)] = 0.001` molar?
View SolutionFor the following first order parallel chain reaction. If the half-life of `A` is `25` seconds, then find out the half-life of `B,C` and `D`. Given that the rate of formation of `B` and `C` is `15%` and `30%` of the rate of decomposition of `A` respectively.
View Solution`._(84)Po^(218) (t_(1//2) = 3.05 min)` decays to `._(82)Pb^(214) (t_(1//2) = 2.68 min)` by `alpha` emisison while `Pb^(214)` is `beta`-emitter. In an experiment starting with `1 g` atom of pure `Po^(218)`, how much time would be required for the concentration of `Pb^(214)` to reach maximum?
View SolutionThe rates of most reaction double when their temperature is raised from `298K` to `308K`. Calculate their activation energy.
View SolutionGiven that the temperature coefficient for the saponification of ethylacetate by `NaOH` is `1.75`. Calculate the activation energy.
View SolutionThe specific rate constant for the decomposition of formic acid is `5.5xx10^(-4) sec^(-1)` at `413 K`. Calculate the specific rate constant at `458K` if the energy of activation is `2.37xx10^(4)` cal `"mol"^(-1)`
View SolutionCalculate the rate constant and half-life period for first order reaction gaving activation energy `39.3 kcal mol^(-1)` at `300^(@)C` and the frequency constant `1.11xx10^(11) sec^(-1)`
View SolutionThe pre-exponential factor for the free radical addition of chloring is `2xx10^(13)s^(-1)`. Find the rate constant of this reaction at `STP`.
View SolutionThe rate constant of a certain reaction is given by:
`log k= 5.4-(212)/(T)+2.17 log T`
Calculate `E_(a) at 127^(@)C`.
View SolutionFor a gaseous reaction, following data is given:
`ArarrB, k_(1)= 10^(15)e-^(2000//T)`
`C rarrD, k_(2) = 10^(14)e^(-1000//T)`
The temperature at which `k_(1) = k_(2)` is
View SolutionConsider the following figure for the reaction:
`A+Brarr M+N`

Answer the following:
(a) Energy level of `(A+B)`
(b) Energy level of `(M+N)`
(c ) Threshold energy level for the reaction.
(d) Energy of activation for the forward reaction.
(e) Energy of activation for the backward reaction.
(f) `DeltaH` or heat of reaction.
View SolutionThe decomposition of `N_(2)O` in `N_(2)` and `O_(2)` in presence of gaseous argon follows II order kinetics having `K=5xx10^(11) e^(-29000//T)`. Find out energy of activation and rate constant at `27^(@)C`. Also evalute Arrhenius parameter.
View Solution`H_(2)O` and `O` atom react in upper atmosphere bimolecularly to form two `OH` radicals. `DeltaH` for the reaction is `72 kJ` at `500K` and energy of activation is `77kJ mol^(-1)`. Estimate `E_(a)` for bimolecular recombination of two `OH` radicals to form `H_(2)O` and `O` atom.
View SolutionFor the given reaction:
`H_(2) + I_(2) rarr 2HI`
Given: `{:(T(K),1//T(K^(-1)),log k,),(769,1.3 xx 10^(-3),2.9,),(67,1.5 xx 10^(-3),1.1,):}`
The activation energy will be
View SolutionThe rate constant of decomposition of methyl nitrite `(K_(1))` and ethyl nitrite `(K_(2))` follow the equations.
`K_(1)(s^(-1))=10^(13)e^([(-152.3xx10^(3))/(RT)Jmol^(-1)])`
and `K_(2)(s^(-1))=10^(14)e^([(-152.3xx10^(3))/(RT)Jmol^(-1)])`
Calculate the temperature at which both have same rate of decomposition if `0.1M` of each is taken and both show `I` order kinetics.
View SolutionThe time required for `10%` completion of a first order reaction at `298 K` is equal to that required for its `25%` completion at `308 K`. If the pre-exponential factor for the reaction is `3.56 xx 10^(9) s^(-1)`, calculate its rate constant at `318 K` and also the energy of activation.
View SolutionThe rate constant of a reaction is `1.5 xx 10^(7)s^(-1)` at `50^(@)C` and `4.5 xx 10^(7) s^(-1)` at `100^(@)C`. Evaluate the Arrhenius parameters `A` and `E_(a)`.
View SolutionA first order reaction `A rarr B` requires activation energy of `70 kJ mol^(-1)`. When a `20%` solution of `A` was kept at `25^(@)C` for `20 min`, `25%` decomposition took place. What will be the percentage decomposition in the same time in a `30%` solution maintained at `40^(@)C` ? (Assume that activation energy remains constant in this range of temperature)
View SolutionA 1st order reaction is 50% complete in 30 minute at `27^(@)C` and in `10` minute at `47^(@)C`. Calculate the:
(a) Rate constant for reaction at `27^(@)C` and `47^(@)C`.
(b) Energy of activation for the reaction.
(c ) Energy of activation for the reverse reaction if heat of reaction is `-50 kJ mol^(-1)`.
View SolutionAt `380^(@)C` , the half-life periof for the first order decompoistion of `H_(2)O_(2)` is `360 min`. The energy of activation of the reaction is `200 kJ mol^(-1)`. Calculate the time required for `75%` decompoistion at `450^(@)C`.
View SolutionA hydrogenation reaction is carried out at `500 K`. If the same reaction is carried out in the presence of a catalyst at the same rate, the temperature required is `400 K`. Calculate the activation energy of the reaction if the catalyst lowers the activation barrier by `20 kJ mol^(-1)`.
View SolutionThe rate constant for the first order decompoistion of a certain reaction is described by the equation
`log k (s^(-1)) = 14.34 - (1.25 xx 10^(4)K)/(T)`
(a) What is the energy of activation for the reaction?
(b) At what temperature will its half-life periof be `256 min`?
View SolutionTwo reaction, `(I)A rarr` Products and `(II) B rarr` Products, follow first order kinetics. The rate of reaction `(I)` is doubled when the temperature is raised form `300 K` to `310K`. The half life for this reaction at `310K` is `30 min`. At the same temperature `B` decomposes twice as fast as `A`. If the energy of activation for reaction `(II)` is twice that of reaction `(I)`, (a) calculate the rate of constant of reaction `(II)` at `300 K`.
View Solutionform the following data for the reaction between `A` and `B`,

(a) Calculate the order of the reaction with respect to `A` and with respect to `B`.
(b) Calculate the rate constant at `300 K`.
( c) Calculate the pre-expontential factor.
View SolutionIn a Arrhenius equation for a certain reaction, the values of `A and E_(a)` ( energy of activation)are `4xx10^(13)s^(-1)` and `98.6KJ mol^(-1)`, respectively. If the reaction of first order at, what temperature will its life periof be `10 min`.
View SolutionThe progress of the reaction `A hArr nB` with time is presented in the figure given below:
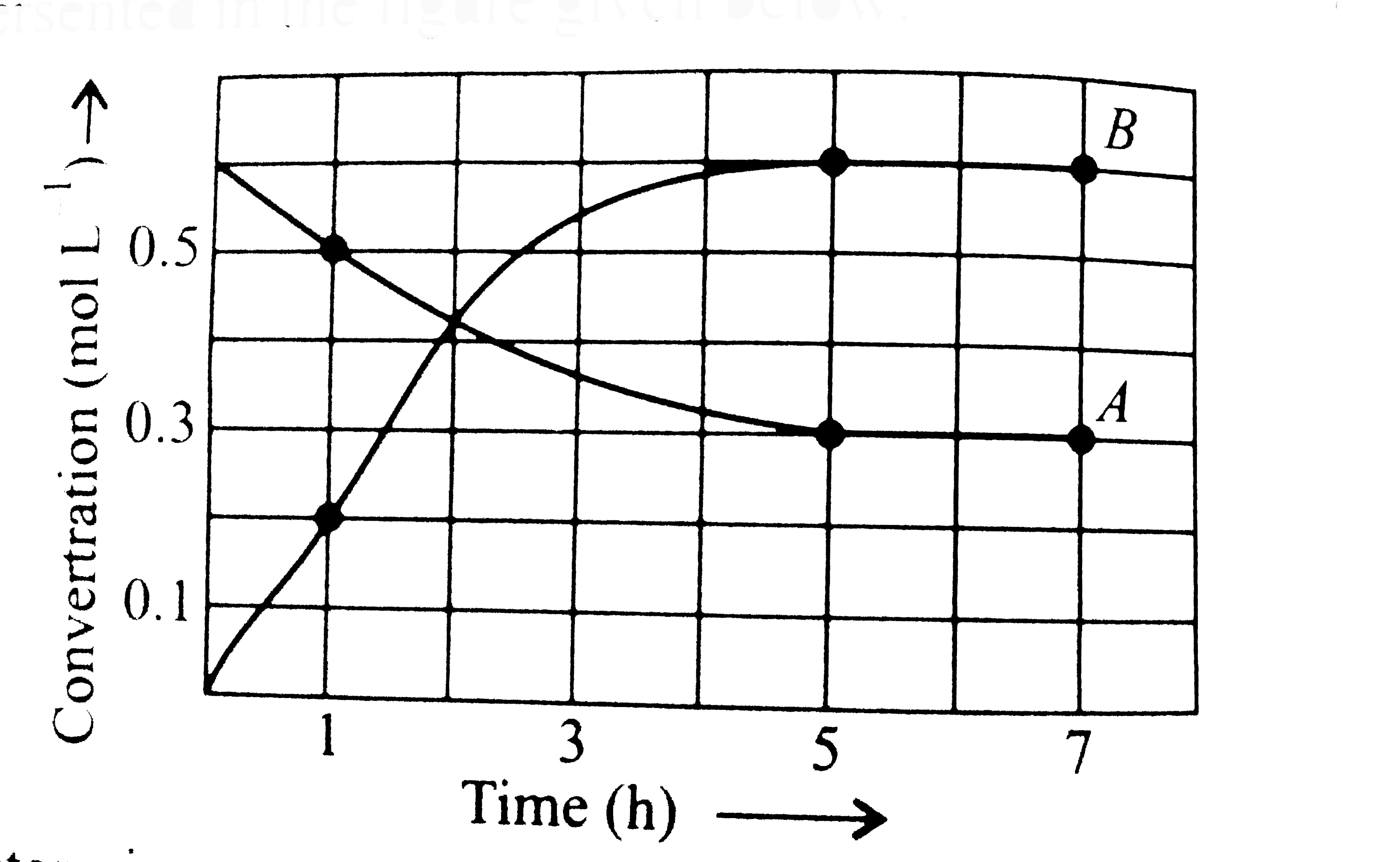
Determine
a. The value of n.
b. The equilibrium constant K.
c. The initial rate of concentration of A.
View SolutionIn a reaction with initially `0.12 M`, the concentration of reactant is reduced to `0.06 M` in `10` hour and to `0.03 M` in `20` hour.
(i) What is order of reaction?
(ii) What is rate constant?
(b) The rate of a first order reaction is `0.04 mol litre^(-1) s^(-1)` at `10` minute and `0.30 mol litre^(-1)` at `20` minute after initiation. Find the half-life of the reaction.
View SolutionThe rate law for the following reactions:
`Ester + H^(o+) rarr "Acid" + "Alcohol"`, is
`dx//dt = k(ester)[H_(3)O^(o+)]^(0)`
What would be the effect on the rate if
(a) concentration of ester is doubled.
(b) concentration of `H^(o+)` ion is doubled.
View SolutionFor the reaction `A+B rarr C`. The following data were obtained. In the first experiment, when the initial concentrations of both `A` and `B` are `0.1 M`, the observed initial rate of formation of `C` is `1xx10^(-4) mol litre^(-1) minute^(-1)`. In the second experiment when the initial concentrations of `A` and `B` are `0.1 M` and `0.3 M`, the initial rate is `9.0xx10^(-4) mol liter^(-1) "minute"^(-1)`. In the third experiment when the initial concentrations of both `A` and `B` are `0.3M` the initial rate is `2.7xx10^(-3) mol litre^(-1) "minute"^(-1)`.
(a) Write rate law for this reaction.
(b) Calculate the value of specific rate constant for this reaction.
View SolutionThe data given below are for the reaction of `NO` and `Cl_(2)` to from `NOCl` at `295 K`.
`{:([Cl_(2)],[NO],,,"Initial rate" (mol litre^(-1) sec^(-1))),(0.05,0.05,,,1xx10^(-3)),(0.15,0.05,,,3xx10^(-3)),(0.05,0.15,,,9xx10^(-3)):}`
(a) What is the order with respect to `NO` and `Cl_(2)` in the reaction ?
(b) Write the rate expression.
(c) Calculate the rate constant.
(d) Determine the reaction rate when conc. of `Cl_(2)` and `NO` are `0.2` M and `0.4` M respectively.
View Solution(a) Write the rate expression. (b) Find the rate constant for
`{:([A]_(0),[B]_(0),,,"`R_(0)` "Rate" (mol litre^(-1) s^(-1))),(0.1,0.2,,,0.05),(0.2,0.2,,,0.10),(0.1,0.1,,,0.05):}`
View SolutionThe following data are for the reaction `A+B rarr` Products:
`{:(Conc. of A(M),,Conc. of B(M),,Initial rate),(,,,,(mol L^(-1) s^(-1))),(0.1,,0.1,,4.0xx10^(-4)),(0.2,,0.2,,1.6xx10^(-3)),(0.5,,0.1,,1.0xx10^(-2)),(0.5,,0.5,,5.0xx10^(-2)):}`
(a) What is the order with respect to `A` and `B` for the reaction?
(b) Calculate the rate constant
Determine the reaction rate when the concentrations of `A` and `B` are `0.2 M` and `0.35 M` respectvely.
View SolutionWhat will be the initial rate of a reaction if its rate constant is `10^(-3) min^(-1)` and the concentration of reactant is `0.2 mol dm^(-3)` ? How much of reactant will be converted into Products in `200 min`?
View SolutionThe rate constant for an isomerization reaction, `A rarr B` is `4.5 xx 10^(-3) min^(-1)`. If the initial concentration of `A` is `1 M`, calculate the rate of the reaction after `1 h`.
View SolutionA substance reacts according to `I` order kinetics and rate constant for the reaction is `1 xx 10^(-2) sec^(-1)`. If its initial concentration is `1M`.
(a) What is initial rate?
(b) What is rate after `I` minute ?
View SolutionThe half time of first order decomposition of nitramide is `2.1` hour at `15^(@)C`.
`NH_(2)NO_(2(aq.))rarr N_(2)O_((g))+H_(2)O_((l))`
If `6.2 g` of `NH_(2)NO_(2)` is allowed to decompose, calculate:
(i) Time taken for `NH_(2)NO_(2)` is decompose `99%`.
(ii) Volume of dry `N_(2)O` produced at this point measured at STP.
View SolutionCatalytic decomposition of nitrous oxide by gold at `900^(@)C` at an initial pressure of `200 mm` was `50%` in `53` minute and `73%` in `100` minute.
(a) What is the order of reaction?
(b) Calculate velocity constant.
(c ) How much will it decompose in `100` minute at the same temperature but at an initial pressure of `600 mm`?
View SolutionThe decompoistion of `N_(2)O_(5)` according to the equation `2N_(2)O_(5)(g) rarr 4NO_(2)(g)+O_(2)(g)`
is a first order reaction. After `30 min`, form the start of the decompoistion in a closed vessel, the total pressure developed is found t be `284.5 mm Hg`. On complete decompoistion, the total pressure is `584.5 mm Hg`. Calculate the rate constant of the reaction.
View SolutionThe decompoistion of `Cl_(2)O_(7)` at `400 K` in gas phase to `Cl_(2)` and `O_(2)` is a first order reaction.
a. After `55 s` at `400 K`, the pressure of `Cl_(2)O_(7)` falls form `0.062` to `0.044 atm`. Calculate `k`.
b. Calculate the pressure of `Cl_(2)O_(7)` after `100 s` of decompoistion.
View SolutionWhile studying the decompoistion of gaseous `N_(2)O_(5)`, it is observed that a plot of logarithm of its partial pressure versus time is linear. What kinetic parameters can be obtained form this observation?
View SolutionThe gas phase decomposition of dimethyl ether follows first order kinetics.
`CH_(3)-O-CH_(3)(g)rarrCH_(4)(g)+H_(2)(g)+CO(g)`
The reaction is carried out in a constant volume container at `500^(@)C` and has a half life of `14.5 min`. Initially, only dimethyl ether is present at a pressure `0.40 atm`. What is the total pressure of the system after `12min`? (Assume ideal gas behaviour)
View SolutionSome `PH_(3)` is introfuced into a flask at `600^(@)C` containing inert gas. `PH_(3)` decomposed to give `P_(4)(g)` and `H_(2)(g)`. The total pressure as a function of time is given below.
`|{:("Time (s)" " "0,60,120,oo),("Pressure (mm) (total) 262.4",272.9,275.53,276.4):}|`
Find the order and half life.
View SolutionThe acid catalysed ionisation of `gamma`-hydroxy butyric acid proceeds as a reversible reaction. Which is I order in both the forward and backward steps:
`underset("(Acid)")(A) underset(K_(1)) overset(K_(2))(hArr) underset("(Lactose)")(B)`
The rate `-(d[A])/(d t)` is given by:
View SolutionFor a certain reaction, a plot of `([C_(0)-C])/(C )` against time `t`, yields a straight line. `C_(0)` and C are concentrations of reaction at `t=0` and `t=t` respectively. The order of reaction is:
View SolutionThe high temperature decomposition of dimethyl ether obeys the first order kinetics.
`{:(,(CH_(3))_(2)O,rarr,CH_(4),+,H_(2),+,CO),("Time (sec)",0,,400,,x,,oo),("Total pressure (mm)",312,,468,,585,,y):}`
The values of `(x, y)` missing above are:
View SolutionFor the reaction, `N_(2)+3H_(2) rarr 2NH_(3)` the rate `(d[NH_(3)])/(dt)=2xx10^(-4) M s^(-1)`. Therefore the rate `-(d[N_(2)])/(dt)` is given as:
View SolutionFor the reaction `N_(2)(g)+3H_(2)(g) rarr 2NH_(3)(g)`, under certain conditions of temperature and partial pressure of the reactants, the rate of formation of `NH_(3)` is `0.001 kg h^(-1)`. The same rate of converison of hydrogen under the same condition is................`kg h^(-1)`.
View SolutionThe rate constant of a second order reaction is `10^(-2) "mol"^(-1) litre sec^(-1)`. The rate constant when expressed in `cm^(3) "molecule"^(-1) min^(-1)` is:
View SolutionThe rate of a reaction gets doubled when the temperature changes from `7^(@)C` to `17^(@)C`. By what factor will it change for the temperature change from `17^(@)C` to `27^(@)C` ?
View SolutionThe rate of a heterogeneous reaction (as iron (solid) any oxygen gas) does not depend on:
View SolutionWhich of the following statement is wrong?
View SolutionThe activation energy of a reaction is zero. The rate constant of this reaction
View SolutionFor the reaction, for which the activation energies for forward and backward reactions are same, then:
View SolutionThe rate constant for a zero order reaction is `2xx10^(-2) mol L^(-1) sec^(-1)`. If the concentration of the reactant after `25 sec` is `0.5 M`, the initial concentration must have been:
View SolutionA consecutive reaction, `A overset(K_(1))(rarr)B overset(K_(2))(rarr)C` is characterised by:
View Solution
Exercise questions and complete solutions for chapter CHEMICAL KINETICS of P BAHADUR CHEMISTRY (HINGLISH) of Class 12