Complete Solutions to Exercise of chapter DUAL NATURE OF RADIATION AND MATTER of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | DUAL NATURE OF RADIATION AND MATTER |
| PRADEEP | Exercise |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The photoelectric effect can be explained on the basis of
View SolutionWhich of the following has minimum stopping potential?
View SolutionWhen radiation is incident on a photoelectron emitter, the potential is found to be 9V. If `e//m` for the electron is `1.8cc10^(11)C//kg`, the maximum velocity of the ejected electron is
View SolutionTwo photons, each of energy 2.5 eV are simultaneously incident on the metal surface. If the work function of the metal is 4.5 eV, then from the surface of metal
View SolutionThe maximum velocity of an electron emitted by light of wavelength `lambda` incident on the surface of a metal of work function `phi`, is
Where h = Planck's constant , m = mass of electron and c = speed of light.
View SolutionThe photoelectric work function for a metal surface is `4.125 eV`. The cut - off wavelength for this surface is
View SolutionThe slope of frequency of incident light and stopping potential for a given surface will be
View SolutionThreshold wavelength for a metal having work function `w_(0)` is `lambda`. Then the threshold wavelength for a metal having work function `2 w_(0)` is
View SolutionThe work function for metals `A , B` and `C` are respectively `1.92 eV , 2.0 eV` and `5 eV`. According to Einstein's equation , the metals which will emit photoelectrons for a radiation of wavelength `4100 Å` are
View SolutionThe wavelength of the matter wave is independent of
View SolutionIf `E_(1), E_(2), E_(3), E_(4)` are the respective kinetic energies of electron, deutron, proton and neutron having same de-Broglie wavelength. Select the correct order in which those values would increases.
View SolutionWhat is de-Broglie wavelength assciated with electron moving under a potential difference of `10^(4)V`.
View SolutionThe minimum energy required by an electron to..........form the metal surface so as to overcome the restraining forces at the surface is called........... .
View SolutionThe maximum kinetic energy of emitted photoelectrons depends on the..........and nature of............but is independent of........ .
View SolutionThe ratio of number of photoelectrons ejected to the number of the photons falling on a metal surface is..........than.......... .
View SolutionFor given photosenstive material, the photoelectric current is.............on decreasing the wavelength of incident radiation, without any change in intensity of radiation.
View SolutionAn increase in the frequency of the incident light.............the velocity with which photoelectron is ejected.
View SolutionThe minimum energy required to ejected an electron from the surface of a metal is called............ .
View SolutionIn photoelectric effect the energy of the free electron does not depend on.............of light.
View SolutionPhoton is not a..........but it is a.......... .
View SolutionThe velocity of photons different media is............. .
View SolutionThe intensity of light depends upon the.........present in light.
View SolutionThe momentum of a photon of energy E is............and of wavelength `lambda` is............. .
View SolutionDe-Broglie wave are associated with a moving particle irrespective of.............on it.
View SolutionThe de-broglie wavelength of a photon of an electromagnetic radiation is..........the wavelength of the radiation.
View SolutionA photon and electron have got same de-Broglie wavelength. Total energy of an electron is............than that of photon.
View SolutionThe expression for de-Broglie wavelength of an electron moving under a potential difference of V volt is.............. .
View SolutionThe main aim of Davisson-Germer experiment is to verify............ .
View SolutionGiven in fig. is the graph between frequency v of the incident light and maximum kinetiec energy `(E_(k))` of the emitted photoelectrons. Find the values of (i) threshold frequency and (ii) work function form the graph.
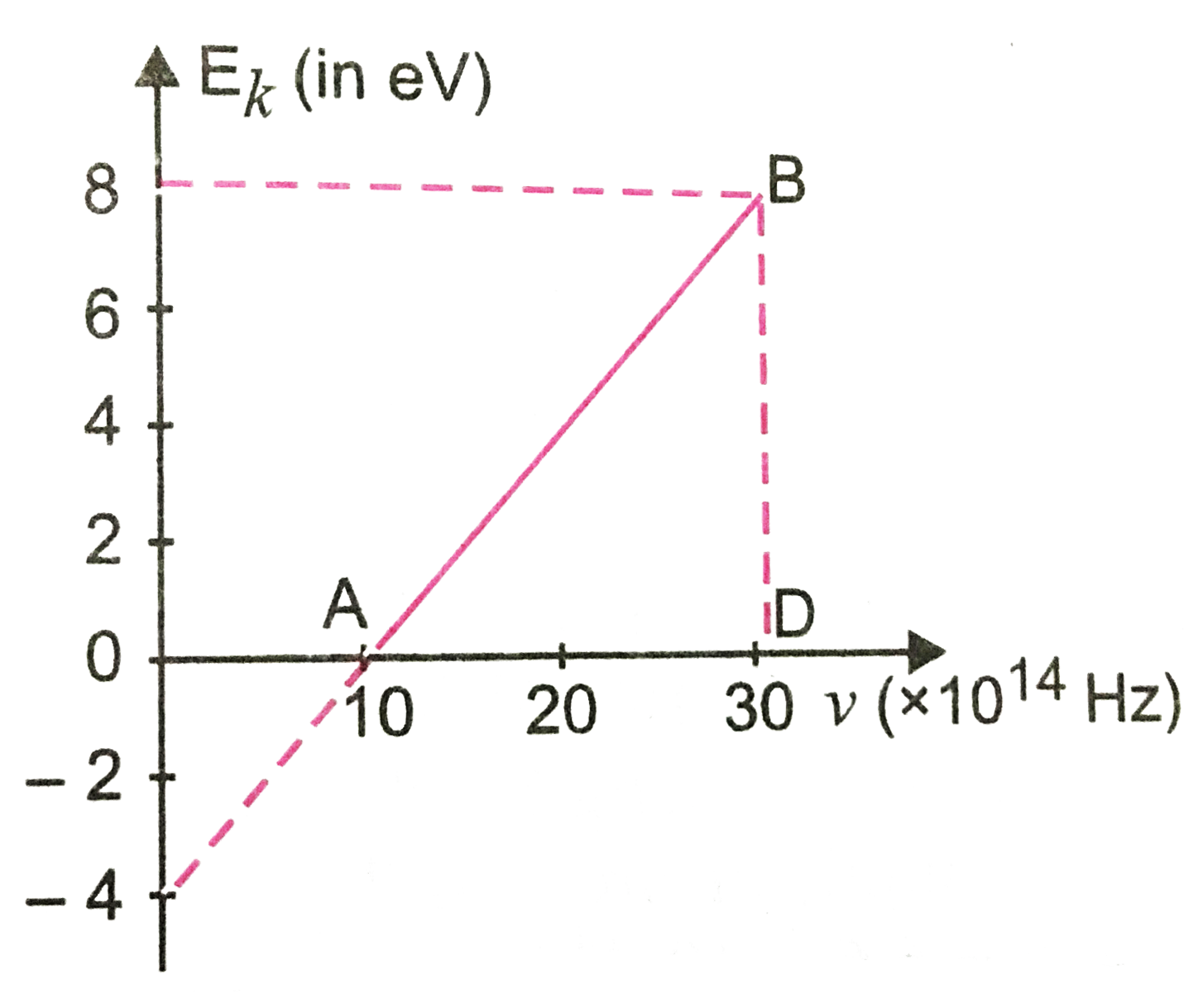
View SolutionFor photoelectric effect in sodium, fig. shows the plot of cut-off voltage versus frequency of the incident radiation. Caclculate:
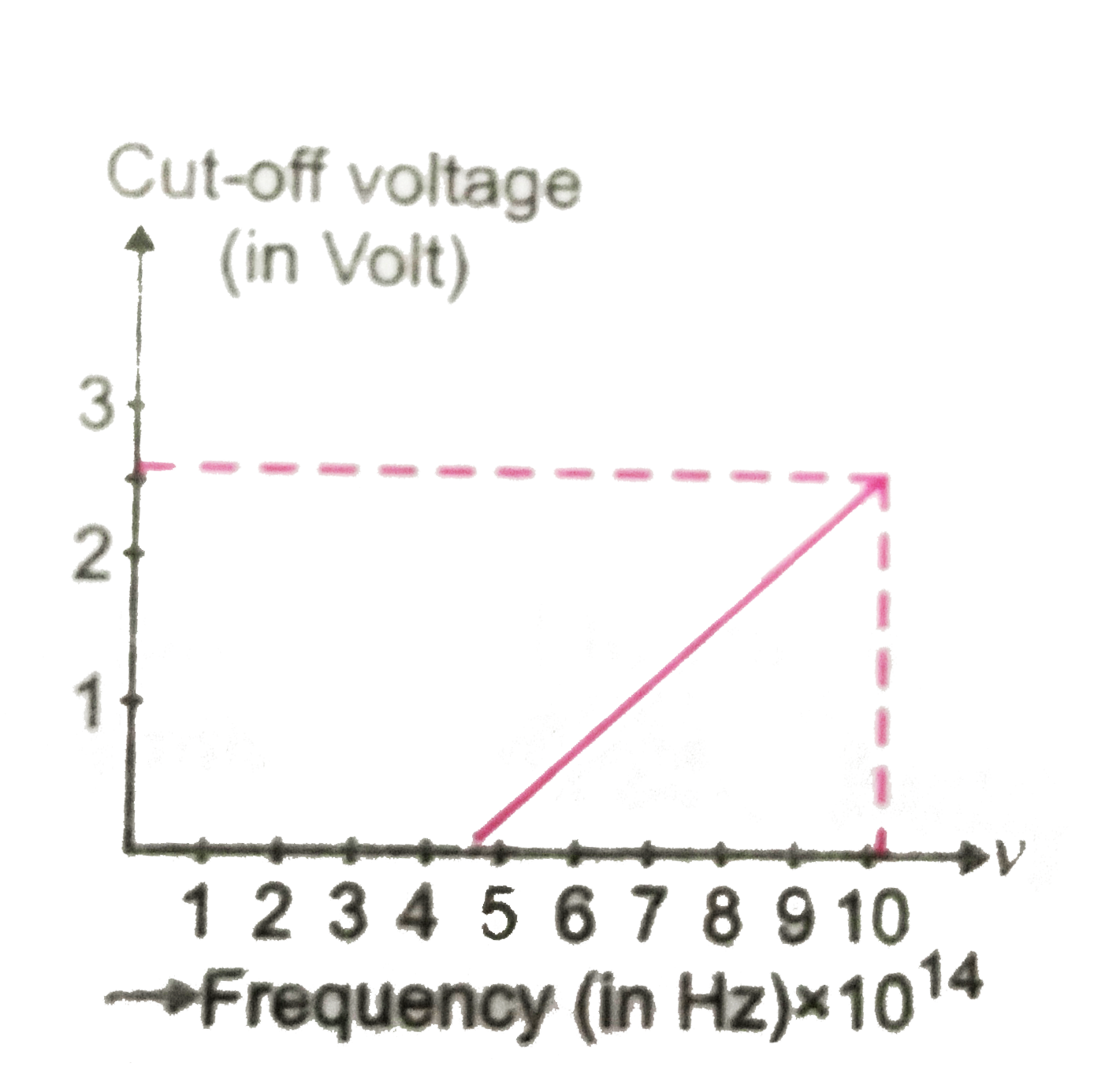
(i) the threshold frequency
(ii) the work function for sodium. (Use `h=6.6xx10^(-34)Js`)
View SolutionWhen light of wavelength 400nm is incident on the cathode of photocell, the stopping potential recorded is 6V. If the wavelength of the incident light is to 600nm, calculate the new stopping potential. [Given `h=6.6xx10^(-34) Js, c=3xx10^(8)m//s , e=1.6xx10^(-19)C`]
View SolutionRadiation of a certain wavelength causes electrons with a maximum kinetic energy of 0.65 eV to be ejected from a metal surface whose work function is 2.65 eV. What will be the maximum kinetic energy (in eV) with which this same radiation ejects electrons from another metal whose work function is 2.15eV.
View SolutionThe electric field associated with a monochromataic beam of light becomes zero, `2.4xx10^(15)` times per second. Find the maximum kinetic energy of the photoelectrons when this light falls on a metal surface whose work function is 2.0eV, `h=6.63xx10^(-34)Js`.
View SolutionUltraviolet light of wavelength `800 A` and `700 A` when allowed to fall on hydrogen atoms in their ground states is found to liberate electrons with kinetic energies `1.8eV` and `4.0eV`, respectively. Find the value of Planck's constant.
View SolutionLight of wavelength `2000 Å` falls on an aluminium surface . In aluminium `4.2 e V` of energy is required to remove an electron from its surface. What is the kinetic energy , in electron volt of (a) the fastest and (b) the slowest emitted photo-electron . ( c) What is the stopping potential ? (d) What is the cut - off wavelength for aluminum? (Plank's constant `h = 6.6 xx 10^(-34) J-s` and speed of light `c = 3 xx 10^(8) m s^(-1).
View SolutionThe maximum wavelength for which an em wave can ejected electrons form a platinum surface is 195 nm. When radiations with a wavelength of 131nm shines on the surface. What is the maximum speed of the ejected electrons? [Use `h=6.63xx10^(-34)Js`] `m_(e)=9.1xx10^(-31)kg`.
View SolutionFind the frequency of light which ejects electrons from a metal surface. Fully stopped by a retarding potential of `3 V`, the photoelectric effect begins in this metal at a frequency of `6xx10^(14)Hz`. Find the work function for this metal. (Given `h=6.63xx10^(-34)Js`).
View SolutionThe work fuction of caseium is 1.8 eV. Light of 4500Å is incident on it. Calculate (i) the maximum kinetic energy of the emitted photoelectrons (ii) maximum velocity of the emitted photoelectrons (iii) if the intensity of the incident light is doubled, then find the maximum kinetic energy of the emitted photoelectrons. Given, `h=6.63xx10^(-34)Js.m_(e)=9.1xx10^(-31)kg, c=3xx10^(8)ms^(-1)`
View SolutionFind the difference of kinetic energies of photoelectrons emitted from a surface by light of wavelength 2500Å and 5000Å. `h=6.62xx10^(-34)Js`.
View SolutionThe electric field associated with a light wave is given by `E=E_(0)sin[(1.57xx10^(7)m^(-1))(ct-x)]`. Find the stopping potential when this light is used in an experiment on a photoelectric effect with the emitter having work function 2.1eV. `h=6.62xx10^(-34)Js`.
View SolutionA photon of wavelength 3310Å falls on a photocathode and an electron of energy `3xx10^(-19)J` is ejected. If the wavelength of the incident photon is changed to 5000Å, the energy of the ejected electron is `9.72xx10^(-20)J`. Calculate the value of Planck's constant and threhold wavelength of the photon.
View SolutionLight of wavelength 180 nm ejects photoelectrons from a plate of metal whose work - function is 2 eV. If a uniform magnetic field of `5xx10^(-5)` T be applied parallel to the plate, what would be the radius of the path followed by electrons ejected normally from the plate with maximum energy.
View SolutionThe maximum velcities of the photoelectrons ejected are v and 2v for incident light of wavelength 400nm and 250nm on a metal surface respectively. Calculate the work function of the metal. Given `h=6.62xx10^(-34)Js and c=3xx10^(8) ms^(-1)`
View SolutionA radio transmitter operates at a frequency of `880 kHz` and a power of `10 kW`. The number of photons emitted per second are
View SolutionThe minimum intensity of light to be detected by human eye is `10^(-10) W//m^(2)`. The number of photons of wavelength `5.6 xx 10^(-7) m` entering the eye , with pupil area `10^(-6) m^(2)` , per second for vision will be nearly
View SolutionFind the number of photons emitted per minute by a 25W source of monochromatic light of wavelength 5000Å. Use `h=6.63xx10^(-34)Js`.
View SolutionMonochromatic light of frequency `5.0xx10^(14)Hz` is produced by a laser. The power emitted is `3.0xx10^(-3)W`. Estimate the number of photons emitted per second on an avearge by the source. Given `h=6.62xx10^(-34)Js`
View SolutionCaculate the number of photons emitted per second by a 10 watt sodium vepour lamp. Assume tha t 90% of the consumed energy is converted into light. Wavelength of sodium light is 590nm. `h=6.62xx10^(-34)Js`
View SolutionA parallel beam of the light is incident normally on a plane surface absorbing 40% of the light and reflecting the rest. If the incident beam carries 10 watt power, find the force exerted by it on the surface.
View SolutionFind the number of photons emitted per second by a 40 W source of monochromatic light of wavelength 6000Å . What is the photoelectric current assuming 5% effeciency of photoelectric effect? Given `h=6.62xx10^(-34)Js and c=3xx10^(8) ms^(-1),e=1.6xx10^(-19)C`
View SolutionAn X-ray tube produces a continuous spectrum of radiation with its short wavelength end at 0.42Å. What is the maximum energy of photon in the radiation? What is the order of accelerating voltage (for electrons) requirement in such a case? `h=6.62xx10^(-34)Js and e=1.6xx10^(-19)C`
View SolutionAn electron and a photon each has a wavelength of 1.0nm. Find (a) their momenta, (b) the energy of the photon , and © the kinetic energy electron.
Take `h=6.63xx10^(-34) Js`.
View SolutionThe de-Broglie wavelength associated with a material particle when it is accelerated through a potential difference of 150V is 1Å. What will be the de-broglie wavelength associated with the same particle when it is accelerted through a potential difference of 1350V?
View SolutionAn electron is accelerated through a potential difference of 64volts. What is the de-broglie wavelength associated with it? To which part of the electromagnetic spectrum does this value of wavelength correspond?
View SolutionA neutron is an unchanged particle of mass `1.67xx10^(-27) kg`. Calculate the de-Broglie wavelength of the neutron moving with a velocity, such that K.E. is 0.04 eV, `h=6.62xx10^(-34)Js`.
View SolutionCalculate the de-Broglie wavelength of an electron of kinetic energy 100 eV. Given `m_(e)=9.1xx10^(-31)kg, h=6.62xx10^(-34)Js`.
View SolutionFrom a cliff that is 10.0m above a lake, a boy (mass 40 kg) jumps from rest, straight down into the water. At the instant, he strikes the water, what is his de-Broglie wavelength? `(g=10ms^(-2)) h=6.62xx10^(-34)Js`
View SolutionThe de-Broglie wavelength of an electron moving with a velocity `1.5xx10^(8) ms^(-1)` is equal to that of a photon. Caculate the ratio of the kinetic energy of the electron to that of photon.
View SolutionCalculate the energy of an electron having de-Broglie wavelength 5500Å. Given, `h=6.62xx10^(-34)Js, m_(e)=9.1xx10^(-31)kg`.
View SolutionAn electron and a photon each have a wavelength of 2.00nm. Find (i) their momenta (ii) the energy of the photon and (iii) the kinetic energy of electron. `h=6.63xx10^(-34)Js`
View SolutionAn `alpha`-particle and a proton are accelerated from rest through the same potential difference V. Find the ratio of de-Broglie wavelength associated with them.
View SolutionThe wavelength of a photon is 1.4Å. It collides with an electron. Its wavelength after collision is 4Å. Calculate the energy of scattered electron. `h=6.62xx10^(-34)Js`
View SolutionFind the energy that should be added to an electron of energy 2eV to reduce its de-Broglie wavelength from 1nm to 0.5nm.
View SolutionThe de-broglie wavelength associated with photon changes by 0.25%. If its momentum is changed by `9xx10^(-26)kgms^(-1)`, find the initial momentum of electron.
View SolutionAn electron is accelerated through a potential difference of 200volts. What is the de-broglie wavelength associated with it? To which part of the electromagnetic spectrum does this value of wavelength correspond?
View SolutionFind the de-Broglie wavelength (in Å) assciated with a photon moving with a velocity 0.5 c, where `c=3xx10^(8)m//s`, rest mass of proton `=1.675xx10^(-27)kg, h=6.6xx10^(-34)Js`.
View SolutionFind the de-Broglie wavelength of an electron in a metal at `12.^(@)C` and compare it with the mean separation between two electrons in a metal which is about `2Å`, Given `h=6.6xx10^(-34) Js, m_(e)=9.1xx10^(-31) kg`. Boltzmann constant `k=1.38xx10^(-23) JK^(-1)`
View SolutionGiven that a photon of light of wavelength 10,000Å has an energy equl to 1.23eV. When light of wavelength 5000Å and intensity `I_(0)` falls on a photoelectric cell and the saturation current is `0.40xx10^(-6)` ampere and the stopping potential is 1.36 volt, then (i)what is the work function? (ii) If intensity of light is made `4I_(0)`, what should be the saturation current and stopping potential?
View SolutionThe maximum KE of photoelectrons emitted from a cetain metallic surface is 30 eV when monochromatic radiation of wavelength `lamda` falls on it. When the same surface is illuminated with light of wavelength `2lamda`, the minimum KE of photoelectrons is found to be 10 eV. (a) Calculate the wavelength `lamda` and (b) determine the maximum wavelength of incident radiation for which photoelectric emission is possible.
View SolutionWhen a beam of `10.6 eV` photons of intensity `2.0 W //m^2` falls on a platinum surface of area `1.0xx10^(-4) m^2` and work function `5.6 eV, 0.53%` of the incident photons eject photoelectrons. Find the number of photoelectrons emitted per second and their minimum and maximum energy (in eV).
Take `1 eV = 1.6xx 10^(-19) J`.
View SolutionWhen a surface is irradiated with light of wavelength `4950 Å`, a photocurrent appears which vanishes if a retarding potential greater than 0.6 volt is applied across the phototube. When a second source of light is used, it is found that the critical potential is changed to 1.1 volt.
if the photoelectrons (after emission form the source) are subjected to a magnetic field of 10 tesla, the two retarding potentials would
View SolutionWhat amount of energy (in eV) should be added to an electron to reduce its de-Broglie its de-Broglie wavelength from 100 to 50 pm? Given `h=6.62xx10^(-34)Js, m_(e)=9.1xx10^(-31)kg`.
View SolutionA particle is droped from a height H. The de-broglie wavelength of the particle as a funciton of height is proportional to
View SolutionThe wavelength of a photon needed to remove a proton from a nucleus which is bound to the nucleus with 1MeV energy is nearly
View SolutionConsider a beam of electrons (each electron with energy `E_(0))` incident on a metal surface kept in an evacuated chamber. Then
View SolutionConsider the fundamental physics for class XII. Suppose the voltage applied to A is increased. The diffracted beam will have the maximum at a value of `theta` that
View SolutionA proton, a neutron, an electron and an `alpha`-particle have same energy. Then their de-Broglie wavelengths compare as
View SolutionAn electron is moving with an initial velocity `vecv=v_(0)hati` and is in a magnetic field `vecB=B_(0)hatj`. Then it's de-Broglie wavelength
View SolutionAn electron of mass `m` with an initial velocity
`vec(v) = v_(0) hat`(i) `(v_(0) gt 0)` enters an electric field
`vec(E ) =- E_(0) hat (i)` `(E_(0) = constant gt 0)` at `t = 0` . If `lambda_(0)` is its de - Broglie wavelength initially, then its de - Broglie wavelength at time `t` is
View SolutionAn electron (mass m) with an initial velocity `vecv=v_(0)hati` is in an electric field `vecE=E_(0)hatj`. If `lambda_(0)h//mv_(0)`. It's de-broglie wavelength at time t is given by
View SolutionRelativistic corrections become necessary when the expresion for the kinetic energy `1/2mv^(2)`, becomes comparable with `mc^(2)`, where m is the mass of the particle. At what de-broglie wavelength will relativistic corrections become important for an electron?
View SolutionTwo particles `A_(1) and A_(2)` of masses `m_(1), m_(2) (m_(1)gtm_(2))` have the same de-broglie wavelength. Then
View SolutionThe de-broglie wavelength of a photon is twice the de-broglie wavelength of an electron. The speed of the electron is `v_(e)=c/100`. Then
View SolutionPhotons absorbed in matter are coverted to heat. A source emitting n photons/ sec of frequency v is used to convert 1kg of ice at `0^(@)C` to water at `0^(@)C`. Then, the time T taken for the conversion
View SolutionA particle moves in a closed orbit around the origin, due to a force which is directed towards the origin. The de-broglie wavelength of the particles varries cyclists between two valuse `lambda_(1), lambda_(2) with lambda_(1)gtlambda_(2)`. Which of the following statements are true?
View SolutionWhen a metallic surface is illuminated with radiation of wavelength `lambda`, the stopping potential is `V`. If the same surface is illuminated with radiation of wavelength `2 lambda` , the stopping potential is `(V)/(4)`. The threshold wavelength surface is :
View SolutionA photoelectric surface is illuminated successively by monochromatic light of wavelength `lambda` and `(lambda)/(2)`. If the maximum kinetic energy of the emitted photoelectrons in the second case is `3` times than in the first case , the work function of the surface of the material is
(`h` = Plank's constant , `c` = speed of light )
View SolutionIf `K_(1) and K_(2)` are maximum kinetic energies of photoelectrons emitted when light of wavelength `lambda_(2) and lambda_(1)` respectively are incident on a metallic surface. `If lambda_(1)=3lambda_(2)` then
View SolutionThe photoelectric threshold wavelength of silver is `3250 xx 10^(-10) m`. The velocity of the electron ejected from a silver surface by ultraviolet light of wavelength `2536 xx 10^(-10) m` is
`(Given h = 4.14 xx 10^(6) ms^(-1) eVs` and `c = 3 xx 10^(8) ms^(-1))`
View SolutionA and B are two metals with threshold frequencies `1.8xx10^(14)Hz and 2.2xx10^(14)Hz`. Two identical photons of energy of 0.825 eV each are incident on them. Then photoelectrons are emitted in take `h=6.6xx10^(-34)j//s`
View SolutionThe fig. shows the variation of photon current with anode potential for a photo-sensitive surface for three different radiation. Let `I_(a), I_(b) and I_(c)` be the intensities and `f_(a), f_(b) and f_(c)` be the frequency for the curves a,b and c respectively.
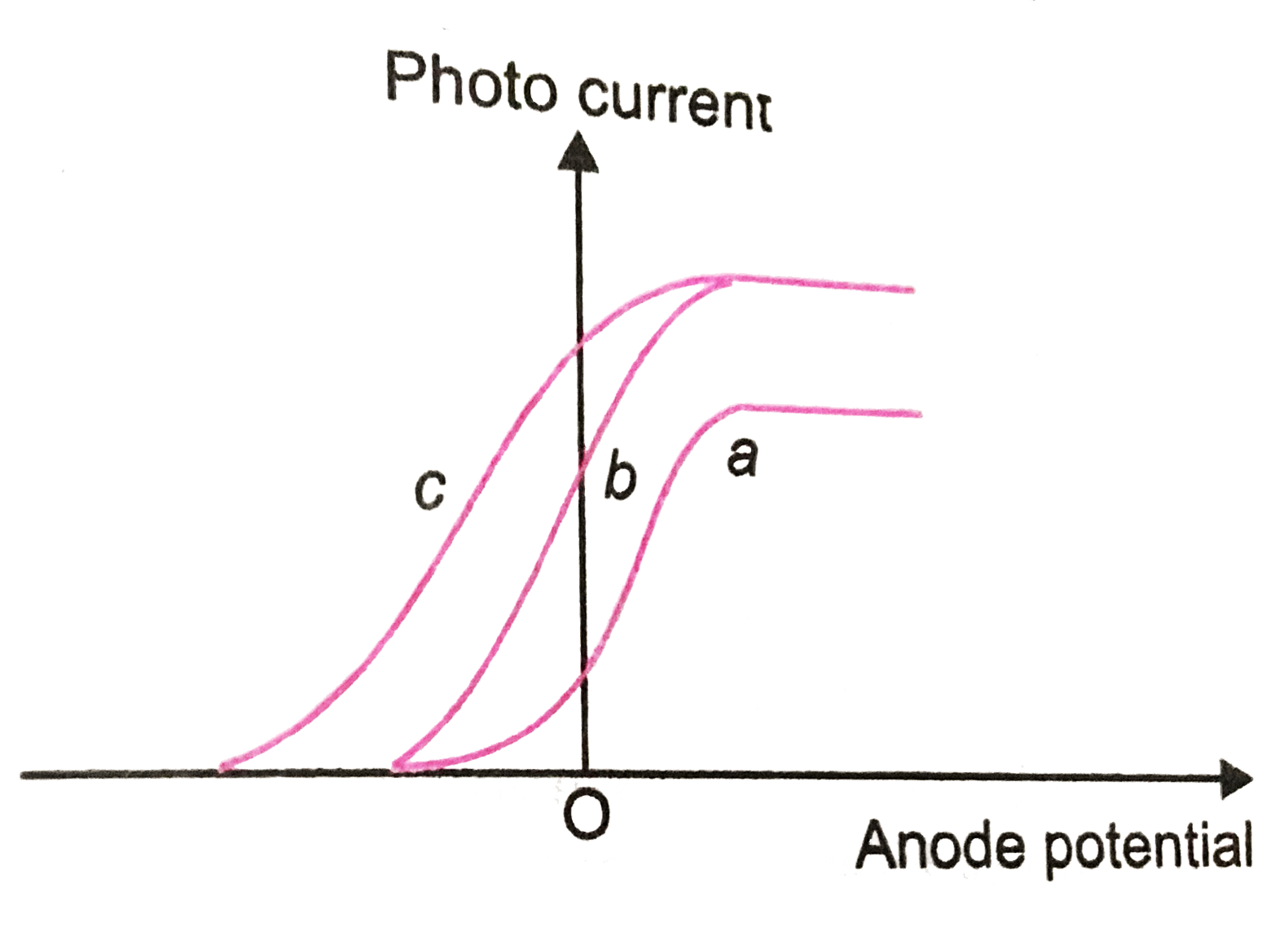
View SolutionThe anode vollage of a photocell is kept fixed . The wavelength `lambda `of the light falling on the cathode varies as follows
View SolutionIn a photoemissive cell, with exciting wavelength `lambda`, the faster electron has speed v. If the exciting wavelength is changed to `3lambda//4`, the speed of the fastest electron will be
View SolutionThe collector plate in an experiment on photoelectric effect is kept vertically above the emitter plate . Light source is put on and a saturation photo current is recorded . An electric field is switched on which has a vertically downward direction . Then

View SolutionWhen a certain metallic surface is illuminated with monochromatic light of wavelength `lamda`, the stopping potential for photoelectric current is `3V_0` and when the same surface is illuminated with light of wavelength `2lamda`, the stopping potential is `V_0`. The threshold wavelength of this surface for photoelectric effect is
View SolutionThe kinetic energy of an electron is E when the incident wavelength is `lamda` To increase ti KE of the electron to 2E, the incident wavelength must be
View SolutionWhen light of wavelength 400nm is incident on the cathode of photocell, the stopping potential recorded is 6V. If the wavelength of the incident light is to 600nm, calculate the new stopping potential. [Given `h=6.6xx10^(-34) Js, c=3xx10^(8)m//s , e=1.6xx10^(-19)C`]
View SolutionA photosenstive metallic surface has work function `hv_(0)`. If photons of energy `3hv_(0)` falls on this surface. The electrons come out with a maximum velocity of `5xx10^(6)m//s`. When the photon energy is increased to `9hv_(0)`. The maximum velocity of photoelectrons will be:
View SolutionMaximum velocity of photoelectrons emitted by a metal surface is `1.2xx10^(6)m//s`. Assuming the specific charge of the electrons to be `1.8xx10^(11)C//kg` the value of stopping potential in volt will be:
View SolutionIf the frequency of light in a photoelectric experiment is doubled the stopping potential will
View Solution
Exercise questions and complete solutions for chapter DUAL NATURE OF RADIATION AND MATTER of PRADEEP PHYSICS (HINGLISH) of Class 12