Complete Solutions to Exercise of chapter RELATIONS AND FUNCTIONS of Class 12 book with complete answers and questions

Determine whether the following relations are reflexive, symmetric and transitive: Relation R in the set `A = {1, 2, 3, ..., 13, 14}` defined as `R = {(x, y) : 3x – y = 0}`

Determine whether the following relations are reflexive, symmetric and transitive:Relation R in the set N of natural numbers defined as `R = {(x, y) : y = x + 5` ਅਤੇ `x < 4}`

Determine whether the following relations are reflexive, symmetric and transitive:Relation R in the set `A = {1, 2, 3, 4, 5, 6}` as `R = {(x, y) : y is divisible by x}`

Prove that the following relation R in Z of integers is an equivalence relation : `R = [ (x, y) : x - y` is an integer}

Determine whether the following relations are reflexive, symmetric and transitive: Relation R in the set A of human beings in a town at a particular time given by, R = {(x, y) : x and y work at the same place}

Determine whether the following relations are reflexive, symmetric and transitive: Relation R in the set A of human beings in a town at a particular time given by, R = {(x, y) : x and y live in the same locality}

Determine whether the following relations are reflexive, symmetric and transitive:Relation R in the set A of human beings in a town at a particular time given by, R = {(x, y) : x is exactly 7 cm taller than y}

Determine whether the following relations are reflexive, symmetric and transitive: Relation R in the set A of human beings in a town at a particular time given by, `R = {(x, y) : x is wife of y}`

Determine whether the following relations are reflexive, symmetric and transitive:Relation R in the set A of human beings in a town at a particular time given by, `R = {(x, y) : x is father of y}`

Show that the relation R in the set R of real numbers, defined as `R = {(a, b) : a le b^2}`, is neither reflexive nor symmetric nor transitive.

Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as `R = {(a, b) : b = a + 1}` is reflexive, symmetric or transitive.

Show that the relation R in the set R of real numbers defined as `R = ((a, b) : a le b}`, is reflexive and transitive but not symmetric.

Check whether the relation R in R defined by R = {(a, b) : a le b^3} is reflexive, symmetric or transitive.

Show that the relation R in the set {1, 2, 3} given by `R = {(1, 2), (2, 1)}` is symmetric but neither reflexive nor transitive.

Show that the relation R in the set A of all the books in a library of a college, given by `R = {(x, y) : x and y have same number of pages}` is an equivalence relation.

Show that the relation in the set `A = { 1 , 2, 3, 4, 5}`, given by : `R = {(a, b): I a- b I is even}` is an equivalence relation. Show that all the elements of {1, 3, 5} are related to each other and all the elements of { 2, 4} are related to each other. But no element of { 1, 3, 5} is related to any element of {2, 4}.

Show that the relation R in the set : `R = {x : x in Z, 0 le x le 1 2}, given by : `R = {(a, b) : |a - b|` is a multiple of 4} is an equivalence relation.

Show that each of the relation R in the set `A = {x in Z : 0 le x le 12}`, given by: `R = {(a, b) : a = b}`, is an equivalence relation. Find the set of all elements related to 1 in each case.

Give an example of a relation. Which is: Symmetric but neither reflexive nor transitive.

Give an example of a relation. Which is: Transitive but neither reflexive nor symmetric.

Give an example of a relation. Which is: Reflexive and symmetric but not transitive.

Give an example of a relation which is reflexive and transitive but not symmetric.

Give an example of a relation which is symmetric and transitive but not reflexive.

Show that the relation R in the set A of points in a plane given by R = {(P, Q) : distance of the point P from the origin is same as the distance of the point Q from the origin}, is an equivalence relation. Further, show that the set of all points related to a point `P ne (0, 0)` is the circle passing through P with origin as centre.

Show that the relation R, defined by the set A of all triangles as : `R = { (T_1, T_2) = T_1` is similar to T_2}` is an equivalence relation. Consider three right-angled triangles T_1 with sides 3, 4, 5, T_2 with sides 5, 12, 1 3 and T_3 with sides 6, 8, 10.

Show that the relation R defined in the set A of all polygons as `R = {(P1, P2) : P1 and P2` have same number of sides}`, is an equivalence relation. What is the set of all elements in A related to the right angle triangle T with sides 3, 4 and 5?

Let T be the set of all triangles in a plane with R a relation in T given by : `R = {(T_1, T_2) : T_1` is congruent to T_2}. Show that R is an equivalence relation.

Let R be the relation in the set {1, 2, 3, 4} given by R = {(1, 2), (2, 2), (1, 1), (4,4), (1, 3), (3, 3), (3, 2)}. Choose the correct answer.

Let R be the relation in the set N given by `R = {(a, b) : a = b – 2, b > 6}`. Choose the correct answer:

Show that the function `f : R_* rarr R_*` defined by `f (x) = 1/x` is one-one and onto, where `R_*` is the set of all non-zero real numbers. Is the result true, if the domain `R_*` is replaced by N with co-domain being same as `R_*`?

Check the injectivity and surjectivity of the following function: `f : NrarrN` given by `f(x) = x^2`

Check the injectivity and surjectivity of the following function: `f : ZrarrZ` given by `f(x) = x^2`

Check the injectivity and surjectivity of the following function: `f : RrarrR` given by `f(x) = x^2`

Check the injectivity and surjectivity of the following function: `f : NrarrN` given by `f(x) = x^3`

Check the injectivity and surjectivity of the following function: `f : ZrarrZ` given by `f(x) = x^3`

Check the injectivity and surjectivity of the following function: `f : RrarrR` given by `f(x) = x^3`

Prove that greatest integer function `f: RrarrR`, given by `f (x) = [x]`, is neither one-one nor onto where [x] denotes the greatest integer less than or equal to x .

Prove that Modulus Function `f: R rarr R` given by : `f(x) = | x |` is neither one-one nor onto, where `| x |` is x, if x is positive and `| x |` is - x, if x is negative.

Show that the Signum Function `f:RrarrR given by f(x) = {(1,,if x>0,,),(0,,if x=0,,),(-1,,if x<0,,):}`, is neither one-one nor onto.

Let `A = {1, 2, 3}, B = {4, 5, 6, 7}` and `f = {(1, 4), (2, 5), (3, 6)}` be a function from A to B. Show that f is one-one.

In the following case, state whether the function is one-one, onto or bijective. Justify your answer: `f:RrarrR` defined by `f(x) = 3-4x`

In the following case, state whether the function is one-one, onto or bijective. Justify your answer: `f:RrarrR` defined by `f(x) = 1+x^2`

Let `f:NrarrN` be defined by, `f(n) = {((n+1)/2,,if n is odd,,),(n/2,,if n is even,,):}` for all `n in N`. State whether the function f is bijective. Justify your answer.

Let` A=R-{3}` and `B=R-{1} `. Consider the function` f:A–>B`. defined by `f(x)= (x-2)/(x-3) `Is f one one or Onto? Justify your answer

Let `f : RrarrR` be defined as `f (x) = 3x` Choose the correct answer.

Let `f : (2, 3, 4, 5} rarr ( 3, 4, 5, 9}` and `g = (3, 4, 5, 9} rarr (7, 11, 15}` be functions defined as: `f(2) = 3`, `f (3) = 4`, `f (4) =f(5) = 5` and `g (3) = g (4) = 7`, and `g (5) = g (1 1 ) = 11`. Find gof

Let f, g and h be functions from R to R. Show that `(f + g)oh = foh + goh` `(f . g)oh = (foh) . (goh)`

Find gof and fog, if `f(x) = |x| and g(x) = |5x -2|`

Find gof and fog, if `f(x) = 8x^3` and `g(x) = x^(1/3)`

If `f(x)=(4x-3)/(6x-4)` ,`x != 2/3 `show that `f@f(x) =x`for all `x != 2/3`.what is inverse of f?

State with reason whether following functions have inverse: `f: {1,2,3,4} rarr {10}` with `f = {(1,10), (2,10), (3,10),(4,10)}`

State with reason whether following functions have inverse: `g: {5,6,7,8} rarr {1,2,3,4}` with `g = {(5,4), (6,3), (7,4),(8,2)}`

State with reason whether following functions have inverse: `h: {2,3,4,5} rarr {7,9,11,13}` with `f = {(2,7), (3,9), (4,11),(5,13)}`

Consider f : R → R given by `f(x) = 4x + 3`. Show that f is invertible. Find the inverse of f.

Consider `f : R_+rarr [4, oo)` given by`f (x) = x^2 + 4` Show that f is invertible with the inverse `f ^–1,of f given by f ^–1(y) = sqrt(y - 4)`, where `R_+` is the set of all non-negative real numbers.

Consider `f : {1, 2, 3} rarr {a, b, c}, given by f (1) = a, f (2) = b and f (3) = c`. Find `f^–1` and show that `(f^–1)^–1 = f`

Let `f : X rarr Y` be an invertible function. Show that the inverse of `f^–1` is f, i.e. `(f^–1)^–1 = f`

If `f : R rarr R, be given by f(x) =(3 - x^3 )^(1/3)` , then `fof (x)` is :

Let `f : R – {4/3}rarrR` be a function defined as `f (x) = 4x/(3x+4)` The inverse of f is the `(Map) g :` Range `f rarr R – {4/ 3}`, given by :

Determine whether or not each of the definition of '*' given below gives a binary operation. In the event that '*' is not a binary operation, give justification for this: `On Z^+, define * by a * b = a - b`

Determine whether or not each of the definition of '*' given below gives a binary operation. In the event that '*' is not a binary operation, give justification for this: `On Z^+, define '*' by a ** b = ab`

Determine whether or not each of the definition of '*' given below gives a binary operation. In the event that '*' is not a binary operation, give justification for this: `On Z^+, define '*' by a ** b = ab^2`

Determine whether or not each of the definition of '*' given below gives a binary operation. In the event that '*' is not a binary operation, give justification for this: `On Z^+, define '*' by a ** b = |a-b|`

Determine whether or not each of the definition of '*' given below gives a binary operation. In the event that '*' is not a binary operation, give justification for this: `On Z^+, define '*' by a ** b = a`

For operation `∗` defined below, determine whether `∗` is binary, commutative or associative: On `Z`, define `a*b=a-b`

For operation `∗` defined below, determine whether `∗` is binary, commutative or associative: On `Q`, define `a*b=ab+1`

For operation `∗` defined below, determine whether `∗` is binary, commutative or associative: On `Q`, define`a*b=ab/2`

For operation `∗` defined below, determine whether `∗` is binary, commutative or associative: On `Z^+`, define`a*b=2^(ab)`

For operation `∗` defined below, determine whether `∗` is binary, commutative or associative: On `Z^+`, define`a*b=a^b`

For operation `∗` defined below, determine whether `∗` is binary, commutative or associative: On `R-{-1}`, define`a*b=a/(b+1)`

Consider the binary operation `^^` on the set `{1, 2, 3, 4, 5}` defined by `a ^^ b = min {a, b}` Write the operation table of the operation `^^`.

Consider a binary operation `∗` on the set `{1, 2, 3, 4, 5}` given by the following multiplication table
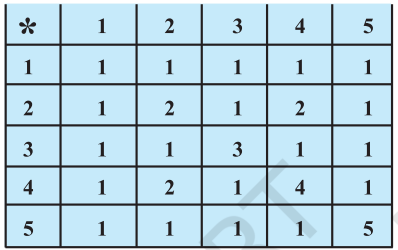: Is `∗` commutative?

Consider a binary operation `∗` on the set `{1, 2, 3, 4, 5}` given by the following multiplication table
:
Compute (2*3)*(4*5)

Let `∗` be the binary operation on N given by `* a * b = L.C.M. of a and b`. Find : `5*7`, `20*16`

Let `∗` be the binary operation on N given by `* a * b = L.C.M. of a and b`. Find : Is `∗` commutative?

Let `∗` be the binary operation on N given by `* a * b = L.C.M. of a and b`. Find : Is `∗` associative?

Let `∗` be the binary operation on N given by `* a * b = L.C.M. of a and b`. Find : Find the identity of `∗` in N

Let `∗` be the binary operation on N given by `* a * b = L.C.M. of a and b`. Find : Which elements of N are invertible for the operation `∗`?

Is `∗` defined on the set `{1, 2, 3, 4, 5}` by `a * b = L.C.M. of a and b` a binary operation? Justify your answer.

Let `∗` be the binary operation on N defined by `a*b=H.C.F. of a and b`. Is `∗` commutative?

Let `∗` be the binary operation on N defined by `a*b=H.C.F. of a and b`. Is `∗` associative?

Let `∗` be the binary operation on N defined by `a*b=H.C.F. of a and b`. Does there exist identity for this binary operation on N?

Let `∗` be a binary operation on the set Q of rational numbers as follows: `a*b=a-b` find is it commutative?

Let `∗` be a binary operation on the set Q of rational numbers as follows: `a*b=a-b` find is it associative?

Let `∗` be a binary operation on the set Q of rational numbers as follows: `a*b=a2-b2` find is it commutative?

Let `∗` be a binary operation on the set Q of rational numbers as follows: `a*b=a2-b2` find is it associative?

Let `∗` be a binary operation on the set Q of rational numbers as follows: `a*b=a+ab` find is it commutative?

Let `∗` be a binary operation on the set Q of rational numbers as follows: `a*b=a+ab` find is it associative?

Let `∗` be a binary operation on the set Q of rational numbers as follows: `a*b=(a-b)^2` find is it commutative?

Let `∗` be a binary operation on the set Q of rational numbers as follows: `a*b=(a-b)^2` find is it associative?

Let `∗` be a binary operation on the set Q of rational numbers as follows: `a*b=a^b/4` find is it commutative?

Let `∗` be a binary operation on the set Q of rational numbers as follows: `a*b=a^b/4` find is it associative?

Let `∗` be a binary operation on the set Q of rational numbers as follows: `a*b=(ab)^2` find is it commutative?

Let `∗` be a binary operation on the set Q of rational numbers as follows: `a*b=(ab)^2` find is it associative?

Let `A = N xx N` and `∗` be the binary operation on A defined by `(a, b) * (c, d) = (a + c, b + d)` Show that `∗` is commutative and associative. Find the identity element for `∗` on A, if any.

State whether the following statement is true or false. Justify:For an arbitrary binary operation `*` on a set `N`, `a * a = a`, `for all a in N`

State whether the following statement is true or false. Justify: If `∗` is a commutative binary operation on N, then`a*(b*c) = (c*b)*a`

Consider a binary operation `∗` on `N` defined as `a * b = a^3 + b^3` Choose the correct answer: Is ∗ neither commutative nor associative?

Consider a binary operation `∗` on `N` defined as `a * b = a^3 + b^3` Choose the correct answer:Is ∗ commutative but not associative?

Consider a binary operation `∗` on `N` defined as `a * b = a^3 + b^3` Choose the correct answer: Is ∗ neither commutative nor associative?