Complete Solutions to PROBLEMS of chapter MOTION ALONG A STRAIGHT LINE of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOTION ALONG A STRAIGHT LINE |
| RESNICK AND HALLIDAY | PROBLEMS |
| Number Of Questions | 53 |
| Academic Year | 2023-24 |
In 25 min, a man ran 2.40 km on a treadmill facing due east. Relative to the gym, what were his (a) displacement and (b) average velocity during this time interval ?
View SolutionCompute your average velocity in the following two cases, (a) You walk 73.2 m at a speed of 1.22 m/s and then run 73.2 m at a speed of 2.85m/s along a straight track. (b) you walk for 1.00 min at a speed of 1.22 m/s and then run for 1.00 min at 3.05 m/s along a straight track. (c) Graph `x` versus t for both cases and indicate how the average velocity is found on the graph.
View SolutionRachel walks on a straight road from her home to a gymnasium 2.80 km away with a speed of 6.00 km/h. As soon as she reaches the gymnasium, she immediately turns and walks back home with a speed of 7.70 km/h as she finds the gymnasium closed. What are the (a) magnitude of average velocity and (b) average speed of Rechel over the interval of time 0.00-35.0 min ?
View SolutionA car travels up a hill at a constant speed of 35 km/h and returns down the hill at a constant speed of 60 km/h. Calculate the average speed for the round trip.
View SolutionThe position of object moving along an x-axis is given by `x=3t-4t^(2)+t^(3)`, where x is in meters and t in seconds. Find the position of the object at the following values of t : (i) 2s, (ii) 4s, (iii) What is the object's displacement between t = 0 s and t = 4 s ? and (iv) What is its average vvelocity for the time interval from t = 2 s to t = 4 ?
View SolutionA pigeon flies at 36 km/h to and for between two cars moving toward each other on a straight road, starting from the first car when the car separation is 40 km. The first car has speed of 16 km/h and the second one has a speed of 25 km/h. By the time the cars meet head on, what are the (a) total distance and (b) net displacement flown by the pigeon ?
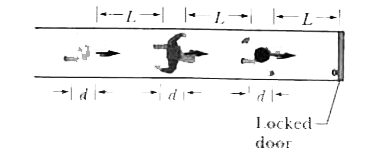
View SolutionPanic escape . Figure 2-16 shows a general situation in which a stream of people attempt to escape through an exit door that turns out to be locked. The people move toward the door at speed `v_(s)=3.50m//s`, are each `d=0.25m` in depth, and are separated by `L=1.75m`. The arrangement in Fig. 2-16 occurs at time `t=0`. (a) At what average rate does the layer of people at the door increase ? (b) At what time does the layer's depth reach 5.0m ? (The answers reveal how quickly such a situation becomes dangerous. )
View SolutionTo set a speed record in a measured ( straight-line) distance d, a race car must be driven first in one direction ( in time `t_(1)`) and then in the opposite direction ( in time `t_(2)` ). (a) To eliminate the effects of the wind and obtain the car's speed `v_(c)` in a windless situation, should we find the average of `d//t_(1)` and `d//t_(2)` ( method 1) or should we find divide d by the average of `t_(1)` and `t_(2)` ? (b) What is the fractional difference in the two methods when a steady wind blows along the car's route and the ratio of the wind speed `v_(w)` to the car's speed `v_(c)` is 0.0240 ?
View SolutionA pickup vehicle is moving with a speed of 15.00 m/s on a straight road. A scooterist wishes to overtake the pickup vehicle in 150.0s. If the pickup vehicle is at an initial distance of 1.500 km from the scooterist, with what constant speed should the scooterist chase the pickup vehicle ?
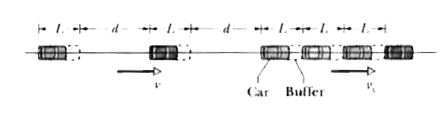
View SolutionTraffic shock wave. An abrupt shlowdown in concentrated traffic can travel as a pulse, termed a shock wave, along the line of cars, either downstream ( in the traffic direction) or upstream, or it can be stationary. Figure 2-17 shows a uniformly spaced line of cars moving at speed `v=25.0` m/s toward a uniformly spaced line of slow cars moving at speed `v_(s)=5.00` m/s. Assume that each faster car adds length `L=12.0` m (car length plus buffer zone ) to the line of slow cars when it joins the line, and assume it slows abruptly at the last instant. (a) For what separation distance d between the faster cars does the shock wave remain stationary ? It the separation is twice that amount, what are the (b) speed and (c) direction ( upstream or downstream ) of the shock wave ?
View SolutionThe displacement of a particle moving along an `x` axis is given by `x=18t+5.0t^(2)`, where `x` is in meters and t is in seconds. Calculate (a) the instantaneous velocity at `t=2.0s` and (b) the average velocity between `t=2.0s` and `t=3.0s`.
View SolutionThe position function `x(t)` of a particle moving along an `x` axis is `x=4.0-6.0t^(2)`, where `x` in meters and t in seconds. (a) At what time and (b) where does the particle ( momentarily) stop ? At what (c) negative time and (d) positive time does the particle pass through the origin ?
View SolutionThe position of a particle moving along an `x` axis is given by `x=12t^(2)-2t^(3)`, where `x` is in meters and t is in seconds. Determine (a) the position, (b) the velocity, and (c) the acceleration of the particle at `t=3.5s`. (d) What is the maximum positive coordinate reached by the particle and (e) at what time is it reached ? (f) What is the maximum positive velocity reached by the particle and (g) at what time is it reached ? (h) What is the acceleration of the particle at the instant the particle is not moving ( other than at `t=0` ) ? (i) Determine the average velocity of the particle between `t=0` and `t=3`s .
View SolutionAt a certain time a particle had a speed of 18 m/s in the positive `x` direction, and 2.4 s later its speed was 30 m/s in the opposite direction. What is the average acceleration of the particle during this 2.4 s interval ?
View Solution(a) If the position of a particle is given by `x=25t-6.0t^(3)`, where `x` is in meters and t is in seconds, when, if ever, is the particle's velocity v zero ? (b) When is its acceleration a zero ? For what time range ( positive or negative ) is a (c) negative and (d) positive ? (e) Graph `x(t), v(t)`, and a(t).
View SolutionA long a straight road, a car moving with a speed of 130 km/h is brought to a stop in a distance of 210 m. (a) Find the magnitude of the deceleration of the car ( assumed uniform ). (b) How long does it take for the car to stop ?
View SolutionA body starting from rest moves with constant acceleration. What is the ratio of distance covered by the body during the fifth second of time to that covered in the first 5.00 s ?
View SolutionA particle confined to motion along an `x` axis moves with constant acceleration from `x=2.0m ` to `x=8.0` m during a 2.5 s time interval. The velocity of the particle at `x=8.0m` is `2.8` m/s. What is the constant acceleration during this time interval ?
View SolutionA muon ( an elementary particle ) enters a region with a speed of `6.00xx10^(6)` m/s and then is slowed at the rate of `1.25xx10^(14)m//s^(2)`. (a) How far does the muon take to stop ? (b) Graph `x` versus t and v versus t for the muon .
View SolutionAn electron, starting from rest and moving with a constant acceleration, travels 2.00 cm in 5.00 ms. What is the magnitude of this acceleration ?
View SolutionOn a dry road, a car with good tires may be able to brake with a constant deceleration of `4.92 m//s^(2)`. (a) How long does such a car, initially traveling at 27.2 m/s, take to stop ? (b) How far does it travel in this time ? (c) Graph `x` versus t and v versus t for the deceleration .
View SolutionA certain elevator cab has a total run of 190 m and a maximum speed of 305 m/min, and it accelerates from rest and then back to rest at `1.22 m//s^(2)`. (a) How far does the cab move while accelerating to full speed from rest ? (b) How long does it take to make the nonstop 190 m run, starting and ending at rest ?
View SolutionThe brakes on your car can slow you at a rate of `5.2m//s^(2)`. (a) If you are going 146 km/h and suddenly see a state trooper, what is the minimum time in which you can get your car under the 90 km/h speed limit ? (The answer reveals the futility of braking to keep your high speed from being detected with a radar or loser gun. ) (b) Graph `x` versus t and v versus t for such a slowing .
View SolutionA rocket, initially at rest, is fired vertically with an upward acceleration of `10.0m//s^(2)` . At an altitude of 0.500 km, the engine of the rocket cuts off. What is the maximum altitude it achieves ?
View SolutionA world's land speed record was set by Colonel John P. Stapp when in March 1954 he rode a rocket-propelled sled that moved along a track at 1020 km/h. He and the sled were brought to a stop in 1.4s. ( See Fig. 2-7.) In terms of g, what acceleration did he experience while stopping ?
View SolutionA stone is thrown from the top of a building with an initial velocity of 20 m/s downward. The top of the building is 60 m above the ground. How much time elapses between the instant of release and the instant of impact with the ground ?
View SolutionIn Fig. 2-18, a red car and a green car, identical except for the color, move toward each other in adjacent lanes and parallel to an `x` axis. At time `t=0`, the red car is at `x_(r)=0` and the green car is at `x_(k)=220m`. If the red car has a constant velocity of 20 km/h, the cars pass each other at `x=44.5` m, and if it has a has a constant velocity of 40 km/h, they pass each other at `x=77.9m`. What are (a) the initial velocity and (b) the constant acceleration of the green car ?

View SolutionIn a particle accelerator , an electron enters a region in which it accelerates uniformly in a straight line from a speed of `4.00xx10^(5)m//s` to a speed of `6.00xx10^(7)m//s` in a distance of 3.00 cm. For what time interval does the electron accelerate ?
View SolutionA car moves along an `x` axis through a distance of 900 m, starting at rest ( at `x=0`) and ending at rest ( at `x=900m`). Through the first `1/4` of that distance, its acceleration is `+2.75m//s^(2)`. Through the rest of that distance, its acceleration is `-0.750m//s^(2)`. What are (a) its travel time through the 900 m and (b) its maximum speed ? (c) Graph position `x`, velocity v, and acceleration a versus time t for the trip.
View SolutionFigure `2-19` depicts the motion of a particle moving along an `x` axis with a constant acceleration. The figure's vertical scaling is set by `x_(s)=6.0m`. What are the (a) magnitude and (b) direction of the particle's acceleration ?
View SolutionA car moving at a constant velocity of 46 m/s passes a traffic cop who is readily sitting on his motorcycle. After a reaction time of 1.0s, the cop begins to chase the spoeding car with a constant acceleration of 4.0 `m//s^(2)`. How much time does the cop then need to overtake the speeding car ?
View SolutionYou are driving toward a traffic signal when it turns yellow. Your speed is the legal speed limit of `v_(0)=55km//h`, your best deceleration rate has the magnitude `a=5.18 m//s^(2)`. Your best reaction time to begin braking is `T=0.75s`. To avoid having the front of your car enter the intersection after the light turns red, should you brake to a stop or continue to move at 55 km/h if the distance to the intersection and the duration of the yellow light are (a) 40 m and 2.8 s, and (b) 32 m and 1.8 s ? Give an answer of brake, continue, either ( if either strategy works ), or neither ( if neither strategy works and the yellow duration is inappropriate ) .
View SolutionOn a defense aircraft carrier, a military jet lands at a speed of 64 m/s. (a) Assuming the acceleration to be constant, what is the acceleration of the jet if it stops in 3.0 s due to the arresting cable that snags it ? (b) If the jet first touches at position `x_(i)=0`, what is its final position along an `x` axis lying under its landing path ?
View SolutionYou are arguing over a cell phone while trailing an unmarked police car by 25 m, both your car and the police car are traveling at 120 km/hr. Your argument diverts your attention from the police car for 2.0 s ( long enough for you to look at the phone and yell, " I won't do that ! " ). At the beginning of that 2.0 s, the police officer begins braking suddenly at `5.0 m//s^(2)`. (a) What is the separation between the two cars when your attention finally returns ? Suppose that you take another 0.40 s to realize your danger and uegin braking . (b) If you too brake at `5.0 m//s^(2)`, what is your speed when you hit the police car ?
View SolutionWhen a high-speed passenger train traveling at 161 km/h rounds a bend, the engineer is shocked to see that a locomotive has improperly entered onto the track from a siding and is a distance `D=676` m ahead ( Fig. 2-20). The locomotive is moving at 29.0 km/h. The engineer of the high-speed train immediately applies the brakes . (a) What must be the magnitude of the resulting constant deceleration if a collision is to be just avoided ? (b) Assume that the engineer is at `x=0` when , at `t=0`, he first spots the locomotive. Sketch `x(t)` curves for the locomotive and high-speed train for the cases in which a collision is just avoided and is not quite avoided.

View SolutionA man releases a stone at the top edge of a tower. During the last second of its travel, the stone falls through a distance of (9/15) H, where H is the tower's height. Find H.
View SolutionRaindrops fall 1800 m from a cloud to the ground . (a) If they were not slowed by air resistance, how fast would the drops be moving when they struck the ground ? (b) Would it be safe to walk outside during a rainstorm ?
View SolutionA hot-air balloon is ascending at a rate of 14 m/s at a height of 98 m above the ground when a packet is dropped from it. (a) With what speed does the packet reach the ground, and (b) how much time does the fall take ?
View SolutionA hoodlum throms a stone vertically downward with an initial speed of 15.0 m/s from the roof of a building, 30.0 m above the ground. (a) How long does it take the stone to reach the ground ? (b) What is the speed of the stone at impact ?
View SolutionA melon is dropped from a height of 39.2 m. After it crosses through half that distance , the acceleration due to gravity is reduced to zero by air drag. With what velocity does the melon hit the ground ?
View SolutionA key falls from a bridge that is 45 m above the water. It falls directly into a model boat, moving with constant velocity, that is 12 m from the point of impact when the key is released . What is the speed of the boat ?
View SolutionA stone is dropped into a river from a bridge 53.6 m above the water. Another stone is thrown vertically down 1.00 s after the first is dropped. The stones strike the water at the same time. (a) What is the initial speed of the second stone ? (b) Plot velocity versus time on a graph for each stone, taking zero time as the instant the first stone is released .
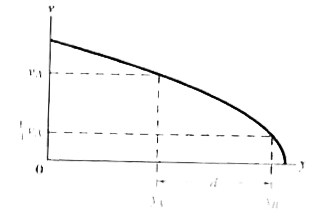
View SolutionFigure 2-21 shows the speed v versus height y of a ball tossed directly upward , along a y axis. Distance d is 0.40 m. The speed at height `y_(A)` is `v_(A)`. The speed at height `y_(B)` is `1/3 v_(A)`. What is speed `v_(A)` ?
View SolutionTo test the quality of a tennis ball, you drop it onto the floor from a height of 4.00 m. It rebounds to a height of 2.00 m. If the ball is in contact with the floor for 12.0 ms, what is its average acceleration during that contact? Take `g= 98 m//s^2.`
View SolutionWater drips from the nozzle of a shower onto the floor 200 cm below. The drops fall at regular ( equal) intervals of time, the first drop striking the floor at the instant the fourth drop begins to fall. When the first drop strikes the floor, how far below the nozzle are the (a) second and (b) third drops ?
View SolutionA rock is thrown vertically upward from ground level at time `t=0`. At `t=1.5s` it passes the top of a tall tower, and 1.0 s later it reaches its maximum height. What is the height of the tower ?
View SolutionA dog sees a flowerpot that sails first up and then down past an open window. The pot is in view for a total of 0.50 s, and the top-to-bottom height of the window is 2.00 m. How high above the window top does the flowerpot go ?
View SolutionA rock is thrown downward from an unknown height above the ground with an initial speed of 10 m/s. It strikes the ground 3.0 s later. Determine the initial height of the rock above the ground .
View SolutionIn a forward punch in karate, the fist begins at rest at the waist and is brought rapidly forward until the arm is fully extended. The speed v (t) of the fist is given in Fig. 2-22 for someone skilled in karate. The vertical scaling is set by `v_(s)=8.0 m//s`. How far has the fist moved at (a) time `t=50` ms and (b) when the speed of the fist is maximum ?

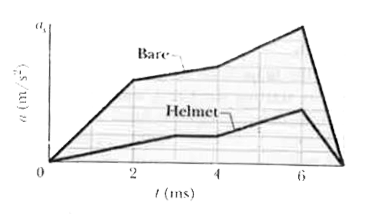
View SolutionWhen a soccer ball is kicked toward a player and the player defiects the ball by " iteading" it, the acceleration of the head during the collision can be significant. Figure 2-23 gives the measured acceleration a(t) of a soccer player's head for a bare head and a helmeted head, starting from rest. the scaling on the vertical axis is set by `a_(s)=200m//s^(2)`. At time `t=7.0` ms, what is the difference in the speed acquired by the bare head and the speed acquired by the helmeted head ?
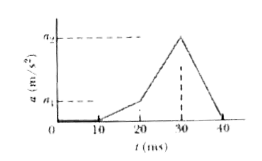
View SolutionA salamander of the genus Hydromantes captures prey by launching its tongue as a projectile: The skeletal part of the tongue is shot forward, unfolding the rest of the tongue, until the outer portion lands on the prey, sticking to it. Figure 2-24 shows the acceleration magnitude a versus time t for the acceleration phase of the launch in a typical situation. The indicated accelerations are `a_(2)=400 m//s^(2)` and `a_(1)=100 m//s^(2)`. What is the outward speed of the tongue at the end of the acceleration phase ?
View SolutionHow for does the runner whose velocity-time graph is shown in Fig. 2-25 travel in 16 s ? The figure's vertical scaling is set by `v_(s)=8.0m//s`.

View SolutionTwo particles move along an `x` axis. The position of particle 1 is given by `x=6.00t^(2) + 3.00 t + 2.00` ( in meters and seconds ) , the acceleration of particle 2 is given by `a= -8.00t` ( in meters per second squared and seconds ) and , at `t=0`, its velocity is . 15 m/s . When the velocities of the particles match, what is their velocity ?
View Solution
PROBLEMS questions and complete solutions for chapter MOTION ALONG A STRAIGHT LINE of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12
All Exercises from RESNICK AND HALLIDAY Class 12 PHYSICS MOTION ALONG A STRAIGHT LINE
- Checkpoints
- PRACTICE QUESTIONS ( Integer Type )
- PRACTICE QUESTIONS ( Linked Comprehension )
- PRACTICE QUESTIONS ( Matrix-Match)
- PRACTICE QUESTIONS ( More than One Correct Choice Type )
- PRACTICE QUESTIONS ( Single Correct Choice Type)
- PROBLEMS
- SAMPLE PROBLEM 2.01
- SAMPLE PROBLEM 2.02
- SAMPLE PROBLEM 2.03
- SAMPLE PROBLEM 2.04
- SAMPLE PROBLEM 2.05
- SAMPLE PROBLEM 2.06
- SAMPLE PROBLEM 2.07
- SAMPLE PROBLEM 2.08
- SAMPLE PROBLEM 2.09
- SAMPLE PROBLEM 2.10