Complete Solutions to Practice Questions (Linked Comprehension) of chapter CIRCUITS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | CIRCUITS |
| RESNICK AND HALLIDAY | Practice Questions (Linked Comprehension) |
| Number Of Questions | 11 |
| Academic Year | 2023-24 |
An electrolytic cell containing a solution of `CuSO_(4)` has an internal resistance of `1Omega.` It is connected in series with 3 V battery of negligible resistance and a `4Omega` resistance. The mass of copper which will be deposited on the copper electrode in 30 min is calculated. If `4 Omega` resistance is connected in parallel across the electrolytic cell and the same battery is used, the amount of copper deposited in 30 min is calculated ECE of Cu= 0.00033 g/C. Using Faraday's first law of electrolysis, the mass deposited on the copper electrode can be calculated.
For series connection of `4 Omega` resistor, the current flowing through electrolyte is
View SolutionAn electrolytic cell containing a solution of `CuSO_(4)` has an internal resistance of `1Omega.` It is connected in series with 3 V battery of negligible resistance and a `4Omega` resistance. The mass of copper which will be deposited on the copper electrode in 30 min is calculated. If `4 Omega` resistance is connected in parallel across the electrolytic cell and the same battery is used, the amount of copper deposited in 30 min is calculated ECE of Cu= 0.00033 g/C. Using Faraday's first law of electrolysis, the mass deposited on the copper electrode can be calculated.
Mass of copper deposited in 30 min when resistance of `4 Omega` is in series is
View SolutionAn electrolytic cell containing a solution of `CuSO_(4)` has an internal resistance of `1Omega.` It is connected in series with 3 V battery of negligible resistance and a `4Omega` resistance. The mass of copper which will be deposited on the copper electrode in 30 min is calculated. If `4 Omega` resistance is connected in parallel across the electrolytic cell and the same battery is used, the amount of copper deposited in 30 min is calculated ECE of Cu= 0.00033 g/C. Using Faraday's first law of electrolysis, the mass deposited on the copper electrode can be calculated.
For the resistance of `4 Omega` connected in parallel to cell, the current in the circuit is
View SolutionAn electrolytic cell containing a solution of `CuSO_(4)` has an internal resistance of `1Omega.` It is connected in series with 3 V battery of negligible resistance and a `4Omega` resistance. The mass of copper which will be deposited on the copper electrode in 30 min is calculated. If `4 Omega` resistance is connected in parallel across the electrolytic cell and the same battery is used, the amount of copper deposited in 30 min is calculated ECE of Cu= 0.00033 g/C. Using Faraday's first law of electrolysis, the mass deposited on the copper electrode can be calculated.
Mass of copper deposited in 30 min when resistance of `4 Omega` is in parallel is
View SolutionThe alternate discs of iron and carbon, having same area of cross-section are cemented together to make a cylinder whose temperature coefficient of resistivity is zero. The change in temperature in two alternate discs is same. The ratio of their thickness and ratio of heat produced in them is found out. The resistivity of iron and carbon at `20^@C` are `1 xx 10^(-7) and 3 xx 10^(-5) Omegam` and their temperature coefficient of resistance are `5 xx 10^(-3)""^(@)C and -7.5 xx 10^(-4)""^(@)C,` respectively. Thermal expansion is neglected. Here, `triangleR_1+ triangleR_2= 0" (where "triangleR_1 and triangleR_2` are the increase in resistances of iron and carbon, respectively, with the rise in temperature) because combined temperature coefficient of resistivity is given as zero.
Ratio of their thickness is
View SolutionThe alternate discs of iron and carbon, having same area of cross-section are cemented together to make a cylinder whose temperature coefficient of resistivity is zero. The change in temperature in two alternate discs is same. The ratio of their thickness and ratio of heat produced in them is found out. The resistivity of iron and carbon at `20^@C` are `1 xx 10^(-7) and 3 xx 10^(-5) Omegam` and their temperature coefficient of resistance are `5 xx 10^(-3)""^(@)C and -7.5 xx 10^(-4)""^(@)C,` respectively. Thermal expansion is neglected. Here, `triangleR_1+ triangleR_2= 0" (where "triangleR_1 and triangleR_2` are the increase in resistances of iron and carbon, respectively, with the rise in temperature) because combined temperature coefficient of resistivity is given as zero.
Ratio of heat produced in them is
View SolutionThe alternate discs of iron and carbon, having same area of cross-section are cemented together to make a cylinder whose temperature coefficient of resistivity is zero. The change in temperature in two alternate discs is same. The ratio of their thickness and ratio of heat produced in them is found out. The resistivity of iron and carbon at `20^@C` are `1 xx 10^(-7) and 3 xx 10^(-5) Omegam` and their temperature coefficient of resistance are `5 xx 10^(-3)""^(@)C and -7.5 xx 10^(-4)""^(@)C,` respectively. Thermal expansion is neglected. Here, `triangleR_1+ triangleR_2= 0" (where "triangleR_1 and triangleR_2` are the increase in resistances of iron and carbon, respectively, with the rise in temperature) because combined temperature coefficient of resistivity is given as zero.
A copper wire is stretched to make it 1% longer. The percentage change in its resistance is
View SolutionA thin uniform wire Ab of length 1m, an unknown resistance X and a resistance of `12 Omega` are connected by thick conducting strips, as shown in the figure. A battery and a galvanometer (with a sliding jockey connected to it) are also available. Connections are to be made to measure the unknown resistance X using the principle of Wheatstone bridge. Answer the following questions.
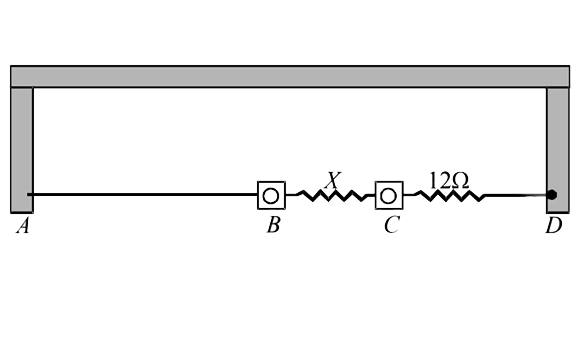
(a) Are there positive and negative terminals on the galvanometer?
(b) Copy the figure in your answer book and show the battery and the galvanometer (with jockey) connected at appropriate points.
View SolutionA thin uniform wire `AB` of length `1m`, an unknown resistance `X` and a resistance of `12 Omega` are connected by thick conducting strips, as shown in the figure. A battery and a galvanometer (with a sliding jockey connected to it) area also available. Connections are to be made to measure the unknown resistance `X` using the principle of Wheatstone bridge. Answer the following questions.

(a) Are there positive and negative terminals on the galvanometer ?
(b) Copy the figure in your answer book and show the battery and the galvanometer (with jockey) connected at apalphariate points.
( c) After apalphariate connections are made, it is found that no deflection takes place in the galvanometer when the sliding jockey touches the wire at a distance of `60 cm` from `A`. Obtain the value of the resistance `X`.
View SolutionA resistor, capacitor, switch, and ideal battery are in series. Originally the capacitor is uncharged. The switch is then closed, allowing current of flow
While the current is flowing, the potential difference across the resistor is
View SolutionA resistor, capacitor, switch, and ideal battery are in series. Originally the capacitor is uncharged. The switch is then closed, allowing current of flow
While the current is flowing, the potential difference across the capacitor is
View Solution
Practice Questions (Linked Comprehension) questions and complete solutions for chapter CIRCUITS of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12