Complete Solutions to साधित उदहारण of chapter फलन of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | फलन |
| SBPD PUBLICATION | साधित उदहारण |
| Number Of Questions | 69 |
| Academic Year | 2023-24 |
मान लीजिएः की कक्षा x के सभी 50 विधार्थियो का समुच्यो A है। मान लीजिएः `f: A to N, f(x)` विद्यार्थियों x का रोल नम्बर, द्वारा परिभाषित एक फलन है। सिद्ध कीजिएः की f एकाकी है किन्तु आच्छादक नहीं है।
03:17View Solutionसिद्ध कीजिए कि एकैकी फलन f : { 1,2,3 } `to` { 1,2,3} अनिवार्य रुप से आच्छादक भी हैं ।
03:00View Solutionसिद्ध कीजिए कि आच्छादक फलन f : { 1,2,3} `to` { 1,2,3} सदैव एकैकी फलन होता हैं ।
03:08View Solutionसिद्ध कीजिए कि f (1) = f(2) = 1 तथा `x gt 2` के लिए f (x) = x - 1 व्दारा प्रदत्त फलन `f : N to N ` आच्छादक तो है कितुं एकैकी नही हैं ।
04:09View Solutionसिद्ध कीजिए की `f(x) = 2x` द्वारा परिभषित फलन `f: N to N` एकेकी है किन्तु आच्छादक नहीं है ।
03:13View Solutionक्या फलन `f : R to R` आच्छादक फलन है जबकि f(x) = 2x | सिद्ध कीजिए कि यह एकैकी है।
02:08View Solutionसिद्ध कीजिए कि नीचे परिभाषित फलन `f : N to N` , एकैकी तथा आच्छादक दोनों ही हैं :
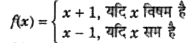 08:29View Solution
08:29View Solutionमाना `f : R to R` एक फलन निम्न प्रकार परिभाषित है
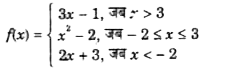
(i) f(2)=?, (ii) f(-3) =?03:28View Solutionयदि `f: R rarr R, f(x)=4x^(3)-7` द्वारा परिभाषित हो, तो दिखाइए कि f एकैकी आच्छादक है |
03:25View Solutionमाना कि A = { 1,2,3 } , B = { 4,5,6,7 } तथा f = { (1, 4 ) , ( 2,5 ) , ( 3,6 ) } A से B तक एक फलन है । सिद्ध कीजिए कि f एकैकी हैं ।
02:02View Solutionनिम्नलिखित में से प्रत्येक स्थिति में बताइये कि क्या दिए गए फलब एकैकी, आच्छादक अथवा एकैकी आच्छादी है? अपने उत्तर का औचित्य भी बताइए।
`f(x)=3-4x` द्वारा परिभाषित फलन `f:RrarrR` है।03:21View Solutionसिद्ध कीजिये कि प्रतिचित्रण `f : R to R` जो `f(x) = cos x , AA x in R` से परिभाषित है न तो एकैकी है और न आच्छादक है।
04:11View Solutionयदि `f : R to R` और `f(x) = (2x)/(2x^(2) + 1)` हो तो `[f((1)/(2))]` ज्ञात कीजिये।
01:21View Solutiongof का मान ज्ञात कीजिये यदि `f : R to R` तथा `g : R to R` फलन `f(x)= cos x` और `g(x) = 3x^(2)`.
01:04View Solutionयदि फलन f : `R to R` इस प्रकार परिभाषित है की `f(x) = (3 - x^(2))^((1)/(2))` तो fof (x) है :
01:46View Solutionतीन फलन `f: N to N, g : N to N` तथा `h : Nto R` पर विचार जहाँ `f(x) = 2x, g(y)= 3y + 4` तथा `h(z) = sin z, AA x =,y ` तथा `z in N` . सिद्ध कीजिए कि `ho(gof) = (hog) of`.
06:24View Solutionमाना कि `f(x)=2x^(2)` तथा `g(x)=3x-4, x in R`, निम्नलिखित का मान ज्ञात कीजिए :
fof(x)02:04View Solutionमाना कि `f(x)=2x^(2)` तथा `g(x)=3x-4, x in R`, निम्नलिखित का मान ज्ञात कीजिए :
gog(x)01:43View Solutionमाना कि `f(x)=2x^(2)` तथा `g(x)=3x-4, x in R`, निम्नलिखित का मान ज्ञात कीजिए :
fog(x)02:19View Solutionमाना कि `f(x)=2x^(2)` तथा `g(x)=3x-4, x in R`, निम्नलिखित का मान ज्ञात कीजिए :
gof(x)01:38View Solutionयदि फलन `f:R toR,f(x)=x^(2)+2` तथा `g:R to R,g(x)=(x)/(x-1),x!=1` द्वारा प्रदत्त है तो `fog (2)` तथा `gof `(-3)`` ज्ञात कीजिए।
04:03View Solutionयदि फलन `f:NtoN` इस प्रकार परिभाषित है कि `f(x)=4x+3`, तो `f^(-1)(x)=`
(a) `4x-3` , (b) `(4x-3)/(2)`
(c ) `(x+3)/(2)` , `(x-3)/(4)`01:42View Solutionमान लीजिए कि `f: N to Y, f (x) =4 x+3` द्वारा परिभाषित एक फलन है, जहाँ `Y= {yin N ,y =4x +3` किसी `x inN` के लिए } सिद्ध कीजिए कि f वियुत्क्रमणीय है । प्रतिलोम फलन भी ज्ञात कीजिए।
04:27View Solutionयदि `f(x) = sin x ` द्वारा प्रदत्त फलन `f : [ 0,pi/2] to R ` तथा `g(x) = cos x ` द्वारा प्रदत्त फलन `g : [ 0,pi/2] to R` पर विचार कीजिए। सिद्ध कीजिए कि f तथा g एकैकी है परन्तु `f+g` एकैकी नहीं है।
09:11View Solution`f(x) = 9x^(2) + 6x -5` द्वारा प्रदत्त फलन `f: R_(+) to [-4,oo)`पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्कमणीय है तथा f का प्रतिलोम `f^(-1),f^(-1)(y) = sqrt(y-4)` द्वारा प्राप्त होता है, जहाँ `R_(+)` सभी ऋणेतर वास्तविक संख्याओं का समुच्चय है।
11:27View Solutionतीन फलन `f: N to N, g : N to N` तथा `h : Nto R` पर विचार जहाँ `f(x) = 2x, g(y)= 3y + 4` तथा `h(z) = sin z, AA x =,y ` तथा `z in N` . सिद्ध कीजिए कि `ho(gof) = (hog) of`.
06:24View Solutionयदि f(x)=x+7 तथा g(x)=x-7, `x inR` हो तो निम्नलिखित के मान ज्ञात कीजिए :
fof(7)01:43View Solutionयदि f(x)=x+7 तथा g(x)=x-7, `x inR` हो तो निम्नलिखित के मान ज्ञात कीजिए :
fog(7)01:43View Solutionयदि `f(x)=x+7` तथा `g(x)=x-7`, `x inR` हो तो निम्नलिखित के मान ज्ञात कीजिए :
`gof(7)`01:35View Solutionयदि f(x)=x+7 तथा g(x)=x-7, `x inR` हो तो निम्नलिखित के मान ज्ञात कीजिए :
gog(7)01:49View Solutionमान लीजिय कि `f : { 2,3,4,5} to { 3,4,59}` और `g :{3,4,5,9} to { 7,11,15}` दो फलन इस प्रकार है कि `f(2) = 3,f(3)= 4,f(4)= f(5) = 5` और `g(3) = g(4) = 7` तथा `g(5) = g(5) = 11`, तो gof ज्ञात कीजिए |
02:18View Solutionयदि `f: R to R ` तथा `g : R to R` फलन क्रमश : `f(x) =cos x ` तथा `g(x) = 3x^(2)` द्वारा परिभाषित है तो gof और fog ज्ञात कीजिए | सिद्ध कीजिए `gof ne fog `
03:23View Solutionयदि `f(x) = (3x + 4)/(5x-7)` द्वारा परिभाषित फलन `f: R -{(7)/(5)} to R-{(3)/(5)}`तथा `g(x) = (7x + 4)/(5x-3)` द्वारा परिभाषित फलन `g : R-{(3)/(5)} to R- {(7)/(5)}` प्रदत है , तो सिद्ध कीजिए कि `fog= I_(A)` तथा `gof = I_(B)`, इस प्रकार कि `I_(A) (X) =x, AAx n A `और `I_(B) (x) = a, AA x in B` जहाँ `A = R - {(3)/(5)}, B= R -{(7)/(5)}` है| `I_(A)` तथा `I_(B)` को क्रमश : समुच्चय A तथा B पर ततसमक (Identity) फलन कहते है |
04:33View Solutionसिद्ध कोजिए कि यदि `f : A to B` तथा `g : B to C` एककी है , तो `gof : A to C` भी एककी है |
03:19View Solutionसिद्ध कीजिए कि यदि `f : A to B` तथा ` g : B to C` आच्छादक है , तो`gof : A to C` भी आच्छादक है।
03:20View Solutionf और g ऐसे दो फलानो पर विचार कीजिए की gof परिभाषित है तथा एकेकी है। क्या f तथा g दोनों अनिवार्यत: एकेकी है ?
04:45View Solutionसत्य/असत्य बताएं
यदि `gof` आच्छादक है, तो क्या f तथा g दोनों अनिवार्यतः आच्छादक है?04:16View Solutionमान लजिए कि `f: {1,2,3} to {a,b,c}` एक एककी तथा अच्छादक फलन इस प्रकार है कि `f(1)=a,f(2) b` और `f(3) = c`, तो सिद्ध कोजिए कि फलन `g: {a,b,c) to {1,2,3}` का ऐसा अस्तित्व है , ताकि `gof = I_(x)` तथा `fog = I_(y)` जहाँ `X = {1,2,3}` तथा `Y = {a,b,c}` हो |
04:38View Solutionमान लीजिए की `Y = {n^(2) : n in N} subset N` है | फलन `F:N to Y` जहाँ `f (n) = n^(2)` पर विचार कोजिए | सिद्ध कीजिए कि f व्युत्क्रमणीय है | f का प्रतिलोम भी ज्ञात कीजिए|
02:32View Solutionमाना f : N `to R , f (x) = 4x^(2) + 12x + 15` व्दारा परिभाषित एक फलन हैं । सिद्ध कीजिए कि f : N`to`S , जहाँ S , जहाँ S , f का परिसर हैं , व्युत्क्रमणीय हैं । f का प्रतिलोम भी ज्ञात कीजिए ।
11:16View Solution`f : (1,2,3) to (a,b,c)` तथा `g : (a,b,c) to` (सेद, गेंद, बिल्ली f(1) = a, f(2) = b, f(3) = c, g(a) = सेब, g(b) = गेंद तथा g(c) = बिल्ली द्वारा परिभाषित फलनों पर विचार कीजिए। सिद्ध कीजिए कि fog और gof व्युत्क्रमणीय है। `f^(-1), g^(-1)` तथा `(gof)^(-1)` ज्ञात कीजिए तथा प्रमाणित कीजिए कि `(gof)^(-1) = f^(-1) og^(-1)` है
08:05View Solutionमान लजिए कि S = { 1,2,3} है | निधर्रित कीजिए कि क्या निचे परिभाषित फलन `f: S to S` का प्रीतमोल फलन है | `f^(-1)`, ज्ञात कीजिए यदि इसका अस्तित्व है |
(a) `f= {(1,1),(2,2),(3,3)}`
(b) `f= { (1,2),(2,1),(3,1)}`
(c) `f={(1,3),(3,2),(2,1)}`03:15View Solution`f(x) = 5x^(2) + 6x - 9` द्वारा प्रदत्त फलन `f : R+ to [-9,oo)` पर विचार कीजिए। सिद्ध कीजिए कि फलन f, `f^(-1) (y) = (sqrt(54+5y)-3)/(5)` के साथ व्युत्क्रमणीय है।
05:33View Solution`f:A rarr B` आच्छादक फलन होगा, यदि
01:24View Solutionf(x) = 2x + 3 द्वारा प्रदत्त फलन `f : R to R` पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है। f का प्रतिलोम फलन भी ज्ञात कीजिए।
03:11View Solution`f:R-{-(4)/(3)}toR-{(4)/(3)}`, जो `f(x)=(4x+3)/(3x+4)` द्वारा प्रदत्त है पर विचार कीजिए। दर्शाइए कि f एकैकी तथा आच्छादक है f का प्रतिलोम फलन ज्ञात कीजिए।
अतः `f^(-1)(0)` ज्ञात कीजिए तथा x ज्ञात कीजिए ताकि `f^(-1)(x)=2`.07:50View Solution`f(x) = 9x^(2) + 6x -5` द्वारा प्रदत्त फलन `f: R_(+) to [-5,oo)` पर विचार कीजिए। सिद्ध कीजिए f व्युत्क्रमणीय है तथा `f^(-1)(y)` = `((sqrt(y+6)-1)/(3))` है
09:33View Solutionएक द्वि-आधारी संक्रिया *, `RxxR` पर निम्न प्रकार परिभाषित है: `(a, b)**(c, d)=(ac, bc+d)`, जहाँ `a,b,c,d in R`। ज्ञात कीजिए `(2, 3) ** (1, -2)`।
01:55View Solutionसमुच्चय {1, 2, 3, 4, 5} में निम्नतम `a^^b`= निम्नतम `{a,b}` द्वारा परिभाषित द्विआधारी संक्रिया पर विचार कीजिए। सक्रिया `^^` के लिए संक्रिया सारणी लिखिए
01:50View Solutionयदि सभी परिमेय संख्याओं के समुच्चय Q में एक द्विचर संक्रिया `*, Q xx Q to Q * (x,y) = x * y = x + y - xy` तो सिद्ध कीजिए कि . साहचर्य है।
03:20View Solutionनिर्धारित कीजिए कीजिए की समुच्चय R में प्रदत निम्नलिखित द्विआधारी संक्रियाओं में से कौन-सी साहचर्य है वे कौन-सी कर्मविनिमेय है?
` a**b =1 AAa,b in R " "(ii ) a**b =(a+b) /( 2) AAa,bin R `04:41View Solutionनिर्धारित कीजिए कि समुच्च R में प्रदत्त निम्नलिखित द्विआधारी संक्रियाओं में से कौन सी साहचर्य है और कौन सी क्रमविनिमेय है |
(a) ` a** b = 1, AA a , b in R `
(b) ` a ** b = ((a + b))/(2) AA, a, b in R `03:22View Solutionएक द्विआधारी संक्रिया `**Z^(+)` पर निम्न रूप परिभाषित है :
`a**b=a^(b)-bजहाँ a,b inZ^(+)`
`2**5` का मान ज्ञात कीजिए , जहाँ `Z^(+)` धनात्मक पूर्णांकों का समुच्चय है ।01:11View Solutionमाना कि N में एक द्वि - आधारी संकिया `**`, `a**b=a` तथा b के LCM द्वारा परिभाषित है , `a,b inN` तब सिद्ध कीजिए कि :`(20**16)**8=20**(16**8)`
02:46View Solutionसिद्ध कोजिए कि R मे योग , अंतर और गुणा द्विआधारी संक्रिया है | किंतु भाग R मे द्विआधारी संक्रिया नहीं है| साथ हे सिद्ध कोजिए कि भाग ऋणेतर वास्तविक संख्याओ के समुच्चय R मे द्विआधारी संक्रिया है।
01:47View Solutionसिद्ध कोजिए कि अंतर (व्यवकलन ) तथा भाग N मे द्विआधारी संक्रिया नहीं है।
03:09View Solutionसिद्ध कोजिए कि `: R xx R to R, (a,b) to a + 4b^(2)` द्वारा प्रदत्त एक द्विआधारी संक्रिया है।
03:10View Solutionमान लीजिए कि P. किसी प्रदन समुच्चय X क समस्त उप समुच्चयों का, समुच्चय सिद्ध कोजिए कि `uu: P xx P to P, (A,B) to A uu B` द्वारा प्रदूत्त तथा `nn : P xx P to P (A,B) to Ann B` द्वारा परिभाषित फलन, P में द्विआधारी संक्रियाएँ हैं।
05:02View Solutionसिद्ध कोजिए कि `(a,b) to ` अधिकतम {a,b} द्वारा परिभाषित `v : R xx R to R ` तथा `(a,b) to ` निम्नतम `{a,b}` द्वारा परिभाषित `^^ : R xx R to R` द्विआधारी संक्रियाएँ हैं।
01:28View Solutionसिद्ध कीजिए कि `+ : Rxx R to R ` तथा `xx : R xx R to R ` क्रमविनिमेय द्विआधारो संक्रियाएँ है, परन्तु ` - : R xx R to R ` तथा `div : R_(**) xxR_(**) to R_(**)` क्रमविनिमेय नहीं है |
03:33View Solutionसिद्ध कीजिए कि `a ** b = a + 2 b ` द्वारा परिभाषित `** : R xx R to R ` क्रमविनिमेय नहीं है |
01:47View Solutionसिद्ध कीजिये कि R में योग तथा गुणा साहचर्य द्विअधारी संक्रियाएँ है । परन्तु व्यवकलन तथा भाग R में साहचर्य नहीं है।
05:37View Solutionसिद्ध कीजिए कि `a** b to a + 2 b ` द्वारा प्रदत्त `** : R xx R to R ` साहचर्य नहीं है |
01:32View Solutionसिद्ध कीजिए कि R में शून्य (0) योग का तत्समक है तथा 1 गुणा का तत्समक है | परंतु संक्रियाओं `-:R xx R to R` और `div : R _(**) xx R_(**) to R_(**)` के लिए कोई तत्समक अवयव नहीं है |
03:54View Solutionसिद्ध कीजिए कि R में धन संक्रिया `'+'` के लिए `-a` का प्रतिलोम a है और R में गुणा संक्रिया `'xx'` के लिए `ane0` का प्रतिलोम `(1)/(a)` है।
04:51View Solutionसिद्ध कीजिए कि N में धन संक्रिया '+' के लिए `a in N` का प्रतिलोम - a नहीं है और N में गुणा संक्रिया `'xx'` के लिए `a in N, a ne 1` का प्रतिलोम `(1)/(a)` नहीं है |
03:06View Solutionमाना की `A = Q xx Q` है तथा A में (a,b), (c,d) `in A` के लिए (a,b) * (c,d) = (ac, b + ad)k द्वारा परिभाषित एक दी-आधारी संक्रिया है। ज्ञात कीजिये की * क्रम-विनिमय तथा साहचर्य है।
06:05View Solutionमाना की A = Q - [1] और A में a * b = a + b + ab द्वारा परिभाषित एक दी-आधारी संक्रिया है। दर्शाइए की * कर्म-विनिमय एवं साहचर्य है A में * का ततसमक अवयव ज्ञात कीजिये तथा का व्युत्क्रमण अवयव भी ज्ञात कीजिये।
07:07View Solutionयदि फलन `f : R to R, f(x) = x^(2)` द्वारा परिभाषित हो तो, दिखाइए की फलन f अनेकीक एकेकी है।
03:03View Solution
साधित उदहारण questions and complete solutions for chapter फलन of SBPD PUBLICATION of Class 12
All Exercises from SBPD PUBLICATION Class 12 MATHS फलन
- अभ्यास 2.1 (दीर्घ उत्तरीय प्रश्न)
- अभ्यास 2.1 (लघु उत्तरीय प्रश्न)
- अभ्यास 2.1 (वस्तुनिष्ठ प्रश्न)
- अभ्यास 2.2 (अति लघु उत्तरीय प्रश्न)
- अभ्यास 2.2 (दीर्घ उत्तरीय प्रश्न)
- अभ्यास 2.2 (लघु उत्तरीय प्रश्न)
- अभ्यास 2.2 (वस्तुनिष्ठ प्रश्न)
- अभ्यास 2.3 ( दीर्घ उत्तरीय प्रश्न)
- अभ्यास 2.3 ( लघु उत्तरीय प्रश्न)
- अभ्यास 2.3 (अति लघु उत्तरीय प्रश्न)
- अभ्यास 2.3 (वस्तुनिष्ठ प्रश्न)
- उच्च स्तरीय बुद्धि कौशल प्रश्न
- एन .सी .आर .टी . एक्सेम्पलर
- एन .सी .आर .टी . एक्सेम्पलर (दीर्घ उत्तरीय प्रश्न)
- एन .सी .आर .टी . एक्सेम्पलर (रिक्त स्थान भरिये)
- एन .सी .आर .टी . एक्सेम्पलर (लघु उत्तरीय प्रश्न)
- एन .सी .आर .टी . एक्सेम्पलर (वस्तुनिष्ठ प्रश्न)
- एन .सी .आर .टी . कार्नर
- कॉम्पिटिशन कॉर्नर
- साधित उदहारण
