Complete Solutions to एन०सी०ई०आर०टी० एक्सेम्पलर (लघु उत्तरीय प्रश्न) of chapter रैखिक प्रोग्रामन of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | रैखिक प्रोग्रामन |
| SBPD PUBLICATION | एन०सी०ई०आर०टी० एक्सेम्पलर (लघु उत्तरीय प्रश्न) |
| Number Of Questions | 26 |
| Academic Year | 2023-24 |
व्यवरोधों `2x+y le 6, x le 2, x ge 0, y ge 0`के अन्तर्गत Z=11x+7y का अधिकतम मान निर्धारित कीजिए |
View Solutionव्यवरोधों `x + y le 1, x ge 0, y ge 0` के अंतर्गत `Z = 3x + 4y` का अधिकतमीकरण कीजिए।
View Solutionव्यवरोधों `x le 3, y le 2, x ge 0, y ge 0` के अंतर्गत `Z = 11x + 7y` फलन का अधिकतमीकरण कीजिए।
View Solutionव्यवरोधों `x + y le 7, 2x - 3y + 6 ge 0, x ge 0, y ge 0` के अंतर्गत `Z = 13 x - 15y` का न्यूनतमीकरण कीजिए।
View Solution`Z = 3x + 4y` का अधिकतम मान ज्ञात कीजिए। यदि LPP का सुसंगत क्षेत्र (छायांकित) आकृति में प्रदर्थि है।

View Solutionकिसी LLP का सुसंगत क्षेत्र (छायांकित) आकृति में प्रदर्शित है। Z = 5x + 7y का न्यूनतम मान ज्ञात कीजिए।

View Solutionकिसी LLP का सुसंगत क्षेत्र आकृति में प्रदर्शित है। Z = 11x + 7y का न्यूनतम मान ज्ञात कीजिए।

View Solutionकिसी LLP का सुसंगत क्षेत्र आकृति में प्रदर्शित है। इस क्षेत्र के प्रत्येक कोणीय बिंदु पर Z = 4x + y का मान निकालिए। Z का न्यूनतम मान ज्ञात कीजिए, यदि उसका अस्तित्व है।
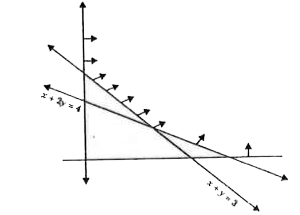
View Solutionआकृति में एक LLP का सुसंगत क्षेत्र (छायांकित) प्रदर्शित है। Z = x + 2y का अधिकतम तथा न्यूनतम मान निकालिए।

View Solutionएक इलेक्ट्रॉनिक परिपथ के निर्माता के पास 200 प्रतिरोधक (resistors), 120 ट्रांजिस्टर तथा 150 संधारित्र (capacitors) का स्टॉक है तथा उसे A और B दो प्रकार के परिपथ का उत्पादन करना है। A प्रकार के परिपथ में 20 प्रतिरोधकों, 10 ट्रांजिस्टर तथा 10 संधारित्रों की आवश्यकता पड़ती है। B प्रकार के परिपथ में 10 प्रतिरोधकों, 20 ट्रांजिस्टरों तथा 30 संधारित्रों की आवश्यकता पड़ती है। यदि प्रत्येक A प्रकार के परिपथ पर लाभ ₹ 50 तथा प्रत्येक B प्रकार के परिपथ पर लाभ ₹ 60 होता है, तो इस समस्या का एक LPP के रूप में सूत्रण कीजिए ताकि निर्माता अपने लाभ का अधिकतमीकरण कर सके।
View Solutionएक फर्म को बड़ी वैनों, जिनमें से प्रत्येक 200 पैकेज तथा छोटी वैनों, जिनमें से प्रत्येक 80 पैकेज ढो सकती है के उपयोग द्वारा 1,200 पैकेज ढोना है। प्रत्येक बड़ी वैन को लगाने पर ₹ 400 तथा प्रत्येक छोटी वैन को लगाने पर ₹ 200 खर्च होते हैं। इस कार्य के लिए ₹ 3,000 से अधिक खर्च नहीं किए जा सकते हैं तथा बड़ी वैन की संख्या छोटी वैन की संख्या से अधिक नहीं हो सकती है। इस समस्या का एक LPP के रूप में सूत्रण कीजिए, यदि यह दिया हुआ है कि उद्देश्य कुल लागत का न्यूनतमीकरण करना है।
View Solutionएक कम्पनी A तथा B, दो प्रकार के पेचों का उत्पादन करती है। सभी पेंचों को एक चूड़ी डालने वाली मशीन तथा एक खाँचा मशीन से होकर गुजरना पड़ता है। A प्रकार के पेचों के एक बक्स को चूड़ी डालने की मशीन के 2 मिनट प्रयोग की तथा खाँचा मशीन के प्रयोग की 3 मिनट की आवश्यकता पड़ती है। B प्रकार के पेचों के लिए एक बक्स को चूड़ी डालने की मशीन के प्रयोग की 8 मिनट तथा खाँचा मशीन के प्रयोग की 2 मिनट की आवश्यकता पड़ती है। प्रत्येक मशीन एक सप्ताह में 60 घण्टे के लिए उपलब्ध है।
इन पेंचों को बेचने पर कम्पनी को A प्रकार के पेंचों पर ₹ 100 प्रति बक्स तथा B प्रकार के पेंचों पर ₹ 170 प्रति बक्स लाभ प्राप्त होता है। इस समस्या का एक LPP के रूप में सूत्रण कीजिए, दिया हुआ है कि उद्देश्य लाभ का अधिकतमीकरण करना है।
View Solutionएक कम्पनी A तथा B दो प्रकार के स्वेटरों का उत्पादन करती है। A प्रकार के एक स्वेटर बनाने में ₹ 360 तथा B प्रकार के एक स्वेटर बनाने में ₹ 120 खर्च होते हैं। कम्पनी प्रतिदिन अधिक-से-अधिक 300 स्वेटर बना सकती है तथा अधिकतम ₹ 72,000 खर्च कर सकती है। B प्रकार के स्वेटरों की संख्या A प्रकार के स्वेटरों की संख्या से 100 से अधिक नहीं हो सकती है। प्रत्येक A प्रकार के स्वेटर पर ₹ 200 B प्रकार के स्वेटर पर ₹ 120 लाभ अर्जित करती है। कम्पनी के कुल लाभ का अधिकतमीकरण करने के लिए इस समस्या का एक LPP के रूप में सूत्रण कीजिए।
View Solutionएक व्यक्ति अपनी मोटर साइकिल को 50 किमी/घ. की रफ्तार से चलाता है। उसे पेट्रोल पर ₹ 2 प्रति किलोमीटर खर्च करने पड़ते हैं। यदि वह 80 किमी/घण्टे की तेज रफ्तार से चलाता है, तो पेट्रोल का खर्च बढ़कर 3 प्रति किलोमीटर हो जाता है। उसके पास पेट्रोल पर खर्च करने के लिए अधिक-से-अधिक ₹ 120 हैं तथा 1 घण्टे का समय है। वह उस अधिकतम दूरी को ज्ञात करना चाहता है, जो वह तय कर सकता है।
इस समस्या को एक रैखिक प्रोग्रामन समस्या के रूप में व्यक्त कीजिए।
View Solutionप्रश्न संख्या 14 पर ध्यान दीजिए। कंपनी को प्रतिदिन, प्रत्येक प्रकार के कितने-कितने स्वेटर बनाने चाहिए जिससे अधिकतम लाभ हो? अधिकतम लाभ कितना है?
View Solutionएक व्यक्ति अपनी मोटर साइकिल को 50 किमी/घ.की रफ्तार से चलाता है। उसे पेट्रोल पर ₹ 2 प्रति किलोमीटर खर्च करने पड़ते हैं। यदि वह 80 किमी/घण्टे की तेज रफ्तार से चलाता है तो पेटोल का खर्च बढ़कर 3 प्रति किलोमीटर हो जाता है। उसके पास पेट्रोल पर खर्च करने के लिए अधिक-से-अधिक ₹ 120 हैं तथा 1 घण्टे का समय है। वह उस अधिकतम दूरी को ज्ञात करना चाहता है जो वह तय कर सकता है। वह अधिकतम दूरी ज्ञात कीजिए जिसे व्यक्ति तय कर सकता है। वह अधिकतम दूरी ज्ञात कीजिए जिसे व्यक्ति तय कर सकता है।
View Solutionएक निर्माता बाइक के दो मॉडल-मॉडल X तथा मॉडल Y बनाता है। मॉडल X की Y की इकाई को बनाने में 10 जन-घण्टे लगते हैं। प्रति सप्ताह कुल 450 जन-घण्टे उपलब्ध हैं। विपणन तथा रख-रखाव पर खर्च मॉडल x की प्रत्येक इकाई तथा मॉडल Y की प्रत्येक इकाई पर क्रमश: ₹ 2,000 तथा ₹ 1,000 हैं। इस कार्य के लिए प्रति सप्ताह कुल उपलब्ध धन ₹ 80,000 है। मॉडल X तथा मॉडल Y की प्रत्येक इकाई पर लाभ क्रमश: ₹ 1,000 तथा ₹ 500 है।
निर्माता को प्रत्येक मॉडल की कितनी बाइक बनानी चाहिए जिससे अधिकतम लाभ मिले? अधिकतम लाभ भी ज्ञात कीजिए।
View Solutionएक व्यक्ति अपने दैनिक आहार के सम्पूरण के लिए कुछ X तथा कुछ Y टिकियाँ (tablets) खाना चाहता है। X तथा Y टिकियों में लौह, कैल्सियम तथा विटामिन के अंश (मिली ग्राम प्रति टिकिया) नीचे दिए गए हैं :

उस व्यक्ति को कम-से-कम 18 mg लौह तत्व, 21 mg कैल्सियम तथा 16 mg विटामिन की आवश्यकता है। प्रत्येक X तथा Y टिकियों का मूल्य क्रमश: ₹ 2 तथा ₹ 1 है। अपनी उपर्युक्त आवश्यकता की पूर्ति के लिए उस व्यक्ति को प्रत्येक प्रकार की कितनी टिकियाँ खानी चाहिए जिससे मूल्य न्यूनतम रहे?
View Solutionएक कम्पनी 3 प्रकार के कैलकुलेटर A, B तथा C अपनी दो फैक्टरियों I तथा II में तैयार करती है। कम्पनी के पास A प्रकार के कम-से-कम 6,400, B प्रकार के कम-से-कम 4,000 तथा C प्रकार के कम-से-कम 4,800 कैलकुलेटरों को तैयार करने का अनुबन्ध है। फैक्टरी I में प्रतिदिन A प्रकार के 50 कैलकुलेटर, B प्रकार के 50 कैलकुलेटर और C प्रकार के 30 कैलकुलेटर तैयार होते हैं, जबकि फैक्टरी II में प्रतिदिन A प्रकार के 40 कैलकुलेटर, B प्रकार के 20 कैलकुलेटर और C प्रकार के 40 कैलकुलेटर तैयार होते हैं। फैक्टरी I को चलाने में प्रतिदिन रु 12,000 का खर्च आता है तथा फैक्टरी II को चलाने में रु 15,000 का। प्रत्येक को कम-से-कम कितने -कितने दिन चलना होगा, जिससे फैक्टरी चलाने का खर्चा न्यूनतम हो, और मांग भी पूरी हो सके। प्रश्न को रेखिक प्रोग्रामन समस्या बनाकर ग्राफ द्वारा हल कीजिए।
View Solutionव्यवरोधों : `x - 2y le 0, -3x + y le 4, x - y le 6, x, y ge 0` के अन्तर्गत `Z = 3x - 4y` का अधिकतमीकरण तथा न्यूनतमीकरण कीजिए।
View Solutionआकृति में किसी का सुसंगत हल प्रदर्शित है। मान लीजिए कि Z = 3x - 4y उद्देश्य फलन है। Z का अधिकतम मान किस बिंदु पर है ?

View Solutionसंलग्न आकृति में किसी LPP का सुसंगत हल प्रदर्शित है।माना `Z = 3x - 4y` उद्देश्य फलन है। Z का न्यूनतम मान किस बिन्दु पर है?
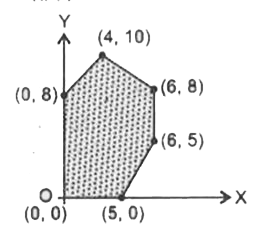
View Solutionआकृति में एक LPP का सुसंगत क्षेत्र प्रदर्शित है। मान लीजिए कि F= 3x - 4y उद्देश्य फलन है। F का अधिकतम मान होगा?

F का न्यूनतम मान है:
View Solutionकिसी LLP के सुसंगत क्षेत्र के कोणीय बिंदु (0, 2), (3, 0), (6,0), (6,8) तथा (0, 5) हैं। मान लीजिए कि `F = 4x + 6y` उद्देश्य फलन है। F का न्यूनतम मान किस बिंदु पर है ?
View Solutionकिसी LPP के सुसंगत क्षेत्र के कोणीय बिन्दु (0,2), (3,0), (6,0),(6,8) तथा (0,5) है | मान लीजिए कि F=4x+6y उद्देश्य फलन है | F का अधिकतम मान `-F` का न्यूनतम मान बराबर है :
View Solutionकिसी राखक व्यवरोधों के निकाय द्वारा निधारित एक सुसंगत क्षत्र क काणाय बिन्दु (0, 3), (1,1) तथा (3, 0) हा मान लीजिए कि Z = px + qy, (जहाँ `p, q gt 0`) उद्देश्य फलन है। p तथा q पर लगने वाला वह प्रतिबन्ध, जिससे Z का न्यूनतम मान (3, 0) तथा (1,1) पर प्राप्त होगा।
View Solution
एन०सी०ई०आर०टी० एक्सेम्पलर (लघु उत्तरीय प्रश्न) questions and complete solutions for chapter रैखिक प्रोग्रामन of SBPD PUBLICATION of Class 12
All Exercises from SBPD PUBLICATION Class 12 MATHS रैखिक प्रोग्रामन
- अभ्यास 12.1
- अभ्यास 12.2 (परिवहन सम्बन्धी समस्या (Transportation Problems) )
- अभ्यास 12.2 (विविध समस्याएँ (Miscellaneous Problems) )
- अभ्यास 12.2 (लघु उत्तरीय प्रश्न )
- उच्च स्तरीय बुद्धि कौशल प्रश्न
- एनसीईआरटी कॉर्नर
- एन०सी०ई०आर०टी० एक्सेम्पलर (रिक्त स्थान भरिये )
- एन०सी०ई०आर०टी० एक्सेम्पलर (लघु उत्तरीय प्रश्न)
- एन०सी०ई०आर०टी० एक्सेम्पलर (वस्तुनिष्ठ प्रश्न)
- एन०सी०ई०आर०टी० एक्सेम्पलर (सत्य/असत्य छाँटिए)
- कम्प्टीशन कॉर्नर
- साधित उदाहरण