Complete Solutions to एन.सी.ई.आर.टी. एक्सेम्पलर (लघु उत्तरीय प्रश्न) of chapter यादृच्छिक चर तथा प्रायिकता बंटन of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | यादृच्छिक चर तथा प्रायिकता बंटन |
| SBPD PUBLICATION | एन.सी.ई.आर.टी. एक्सेम्पलर (लघु उत्तरीय प्रश्न) |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
किसी असंतत यादृच्छिक चर X का प्रायिकता बंटन नीचे दिया हुआ है:

k का मान ज्ञात कीजिए।
View Solutionयदि यादृच्छिक चर X किसी सिक्के को तीन बार उछालने पर 'पट' आने की संख्या को निरूपित करता है, तो X का मानक विचलन ज्ञात कीजिए।
View Solutionकिसी लॉटरी के 10,000 टिकटों में से प्रत्येक को ₹ 1 का बेचा जाता है। प्रथम पुरस्कार ₹ 3,000 का है तथा द्वितीय पुरस्कार ₹ 2,000 का है। इनके अतिरिक्त ₹ 500 वाले तीन अन्य पुरस्कार हैं। यदि आप एक टिकट खरीदते हैं, तो आप को प्रत्याशा (expectation) क्या होगी ?
View Solutionएक यादृच्छिक चर X के नीचे दिये गए प्रायिकता बंटन पर विचार कीजिए।

X का प्रसरण को परिकलित कीजिए।
View Solutionकिसी यादृच्छिक चर X का प्रायिकता बंटन नीचे दिया है।
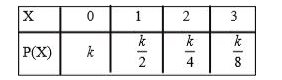
k का मान निर्धारित कीजिए,
View Solutionनिम्नलिखित प्रायिकता बंटन के लिए यादृच्छिक चर X का मानक विचलन निर्धारित कीजिए :

View Solutionएक अनभिनत पासा इस प्रकार का है कि `P(4)=(1)/(10)` तथा अन्य स्कोर सम सम्भाव्य हैं। पासा दो बार उछाला जाता है। यदि 'पासे पर 4 प्रकट होने की संख्या' X है, तो यादृच्छिक चर X का प्रसरण ज्ञात कीजिए।
View Solutionएक पासा तीन बार फेंका जाता है। मान लीजिए कि पासे पर 2 आने की संख्या X द्वारा निरूपित होती है। X की प्रत्याशा (expectation) ज्ञात कीजिए।
View Solutionदो अभिनत पासे एक साथ फेंके जाते हैं। पहले पासे के लिए `P(6) =(1)/(2)`, अन्य स्कोर समसम्भाव्य हैं, जबकि दूसरे पासे के लिए `P(1) = (2)/(5)` तथा अन्य स्कोर समसम्भाव्य हैं। '1 के प्रकट होने की संख्या' का प्रायिकता बंटन ज्ञात कीजिए।
View Solutionदो असंतत यादृच्छिक चर X तथा Y के प्रायिकता बंटन निम्नलिखित हैं :

सिद्ध कीजिए कि : `E(Y^(2))=2E(X)`
View Solutionजब एक पासे को दो बार फेंका जाता है तो प्राप्त दो स्कोरों में से महत्तम स्कोर का प्रायिकता बंटन ज्ञात कीजिए। बंटन का माध्य भी निर्धारित कीजिए।
View Solutionएक यादृच्छिक चर X केवल 0, 1, 2 मानों को धारण कर सकता है। दिया हुआ है कि `P(X=0)=P(X=1)=p` तथा यह कि `E(X^(2))=E[X]`, तो p का मान ज्ञात कीजिए।
View Solutionनिम्नलिखित बंटन का प्रसरण ज्ञात कीजिए :

View Solution
एन.सी.ई.आर.टी. एक्सेम्पलर (लघु उत्तरीय प्रश्न) questions and complete solutions for chapter यादृच्छिक चर तथा प्रायिकता बंटन of SBPD PUBLICATION of Class 12
All Exercises from SBPD PUBLICATION Class 12 MATHS यादृच्छिक चर तथा प्रायिकता बंटन
- अभ्यास 15.1 (दीर्घ उत्तरीय प्रश्न)
- अभ्यास 15.1 (लघु उत्तरीय प्रश्न)
- अभ्यास 15.1 (वस्तुनिष्ठ प्रश्न)
- अभ्यास 15.2 (लघु उत्तरीय प्रश्न)
- अभ्यास 15.2 (वस्तुनिष्ठ प्रश्न)
- उच्च स्तरीय बुद्धि कौशल प्रश्न
- एन.सी.ई.आर.टी. एक्सेम्पलर (दीर्घ उत्तरीय प्रश्न)
- एन.सी.ई.आर.टी. एक्सेम्पलर (रिक्त स्थान भरिये)
- एन.सी.ई.आर.टी. एक्सेम्पलर (लघु उत्तरीय प्रश्न)
- एन.सी.ई.आर.टी. एक्सेम्पलर (वस्तुनिष्ठ प्रश्न)
- एन.सी.ई.आर.टी. एक्सेम्पलर (सत्य/असत्य छाँटिये)
- एनसीईआरटी कॉर्नर
- कम्पटीशन कॉर्नर
- साधित उदाहरण