Complete Solutions to वस्तुनिष्ठ प्रश्न of chapter विद्युत् आवेश तथा क्षेत्र of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | विद्युत् आवेश तथा क्षेत्र |
| SHIVLAAL PUBLICATION | वस्तुनिष्ठ प्रश्न |
| Number Of Questions | 82 |
| Academic Year | 2023-24 |
एक वस्तु पर 80 माइक्रो कूलॉम ऋण आवेश है। उस पर सामान्य अवस्था से अधिक इलेक्ट्रॉनों की संख्या होगी :
View Solution1 कूलॉम आवेश में इलेक्ट्रॉनों की संख्या होती है:
View Solutionकाँच की छड़ को जब रेशम से रगड़ा जाता है तो वह :
View Solutionमुक्त आकाश के परावैद्युतांक `epsilon_(0)` का विमीय सूत्र है :
View Solutionनिर्वात् की विद्युत्शीलता का मान होता है :
View Solutionवायु का परावैद्युतांक है :
View Solutionनिर्वात् में रखे दो आवेशों के मध्य विद्युत् बल F है। यदि दोनों आवेशों के मध्य ताँबे की पट्टी रख दी जाए तो उनके बीच बल होगा :
View Solutionकल्पना कीजिए कि एक प्रोटॉन और एक इलेक्ट्रॉन के आवेश में अल्प अन्तर होता है। इनमें से एक -e है और दूसरा `(e+ Deltae)` है। यदि एक दूसरे से 'd' दूरी पर रखे हाइड्रोजन के दो परमाणुओं के बीच (जहाँ d परमाणु के साइज से बहुत अधिक है) स्थिर वैद्युत बल और गुरुत्वीय बल का परिणामी (नैट) शून्य है तो, `Deltae` की कोटि होगीः (दिया है हाइड्रोजन का द्रव्यमान `m_(h) = 1.67 xx 10^(-27)` किग्रा)
View Solutionएक चालक गोले पर आवेश - 50e है तथा दूसरे समान गोले पर आयेश + 20e है। यदि दोनों गोलों का स्पर्श कराकर अलग कर दिया जाए, तो प्रत्येक पर आवेश होगा :
View Solutionसमान त्रिज्या के दो छोटे सुचालक गोलों पर विद्युत आवेश क्रमशः `+ 10 muC` तथा `-20 muC` हे तथा एक-दूसरे से दूरी R पर रखने पर बल `F_(1)` लगाते हैं। यदि उन्हें आपस में सम्पर्क में लाने के बाद उतनी ही दूरी पर रखने पर वे बल `F_(2)` लगाते हैं, तो `F_(1)` व `F_(2)` का अनुपात है :
View Solutionदो आवेशों Q व Q के ठीक बीचों-बीच एक तीसरा आवेश Q रखा जाता है तो तीसरा आवेश होगा :
View Solutionएक वर्ग के तीन कोनों पर तीन बराबर परिमाण के आवेश रखे हैं। यदि `q_(1)` और `q_(2)` के मध्य बल `F_(12)` और `q_(1)` और `q_(3)` के मध्य बल `F_(13)` हो तो `F_(12)` तथा `F_(13)` के परिमाणों का अनुपात होगा :
View Solutionदो समान गोले जिन पर आवेश + q और -q हैं, कुछ दूरी पर रखे हैं। उनके बीच बल F लगता है। यदि दोनों गोलों के बीच आवेश + q का एकसमान आवेशित गोला रखा जाए तो उस पर लगने वाले बल का मान व दिशा होगी :
View Solutionकिसी उभयनिष्ठ बिंदु से, लम्बाई l की दो द्रव्यमानहीन डोरियों से निलंबित, दो सर्वसम आवेशित गोले, अन्योन्या प्रतिकर्षण के कारण, आरम्भ में एक-दूसरे से `d (d lt lt l)` दूरी पर है। दोनों ही गोलों से एक नियत दर से आवेशों का क्षरण आरम्भ होता हैऔर इसके परिणामस्वरूप गोले एक-दूसरे की ओर वेग v से आते है तब गोलों की बीच की दूरी x के फलन के रूप में वेग से v विचरण किस रूप में होता है?
View Solutionदो छोटी गोलाकार गेंदें, जिनमें प्रत्येक पर आवेश Q = 10 uC है, एक-एक मीटर लम्बाई के दो कुचालक धागों की सहायता से छत पर एक बिन्दु से लटकायी जाती हैं। साम्यावस्था में ये धागे एक-दूसरे से कोण 60° पर पृथक् हो जाते हैं । प्रत्येक धागे में तनाव होगा :

View Solutionदो एक जैसे आवेशित गोले बराबर लम्बाई के दो धागों से लटकाये जाते हैं। धागे एक-दूसरे से कोण 30° बनाते हैं। जब गोलों को 0.8 ग्राम/`("सेमी")^(3)` घनत्व वाले द्रव में डुबा दिया जाता है, तब भी धागों के बीच कोण समान रहता है। यदि गोलों के पदार्थ का घनत्व 16 ग्राम/`("सेमी")^(3)` है तो द्रव का परावैद्युतांक होगा :
View Solutionकिसी बिन्दु आवेश से दूरी r पर विद्युत् क्षेत्र अनुक्रमानुपाती होता है:
View Solutionविद्युत् क्षेत्र की तीव्रता का मात्रक है :
View Solutionविद्युत् क्षेत्र में प्रवेश करने पर, एक आवेशित कण पर लगने वाले बल का परिमाण निर्भर करता है :
View Solutionवह बिन्दु आवेश जिसके कारण 30 सेमी दूर विद्युत् क्षेत्र की तीव्रता 2 न्यूटन/कूलॉम है, होगा :
View Solutionवायु में रखे दो आवेश एक-दूसरे को बल `10^(-4)` न्यूटन से प्रतिकर्षित करते हैं। जब आवेशों के बीच तेल डाल दिया जाता है तो यह बल `2.5 xx 10^(-5)` न्यूटन हो जाता है । तेल का परावैद्युतांक है:
View Solutionहाइड्रोजन परमाणु में प्रोटॉन से इलेक्ट्रॉन की दूरी `10^(-10)` मीटर है। इलेक्ट्रॉन पर प्रोटॉन के कारण उत्पन्न विद्युत् क्षेत्र की तीव्रता का मान होगा :
View Solutionएक इलेक्ट्रॉन व एक प्रोटॉन एकसमान विद्युत् क्षेत्र में स्थित हैं। उनके त्वरणों का अनुपात होगा :
View Solution`10^(-5)` सेमी त्रिज्या वाली जल की एक बूँद पर एक इलेक्ट्रॉन का आवेश है। उसे वायु में निलम्बित करने के लिए आवश्यक विद्युत् क्षेत्र की तीव्रता होगी (लगभग) :
View Solutionएक प्रोटॉन व एक इलेक्ट्रॉन समान विद्युत् क्षेत्र में रखे जाते हैं तो :
View SolutionX-अक्ष पर x = - a तथा x = a पर दो समान आवेश, प्रत्येक q रखे जाते हैं। मूल बिन्दु पर m द्रव्यमान तथा `q_(0) = q//2` आवेश का कण रखा जाता है। यदि कण को Y-अक्ष के अनुदिश थोड़ा-सा विस्थापन `y (y ltlt a)` दिया जाए तो कण पर लगने वाला बल अनुक्रमानुपाती होगा :
View Solutionएक इलेक्ट्रॉन एक विद्युत् क्षेत्र में इस प्रकार प्रवेश करता है कि उसका वेग, विद्युत् क्षेत्र रेखाओं की दिशा में ही है। ऐसी परिस्थिति में :
View Solutionएक आवेश Q को दो भागों q और Q-q में विभाजित किया जाता है। अलग करने पर दोनों आवेशों के बीच का कूलॉम प्रतिकर्षण बल अधिकतम तब होगा जब अनुपात Q/q का मान होगा :
View Solutionदो बराबर आवेश वाले कण एक-दूसरे से दूरी d पर स्थित हैं। इसके लम्ब-अर्द्धक पर दूरी x पर स्थित तीसरे आवेशित कण पर लगने वाला कूलॉम बल अधिकतम होगा, जबकि :
View Solutionधातु के एक ऋणावेशित छोटे गोले को दो बराबर तथा विपरीत बिंदु आवेशों के ठीक बीच में रखा जाता है। यदि गोले को धनावेश की दिशा में थोड़ा-सा हटाकर छोड़ दें तो
View Solutionभुजा a बाले एक समबाहु त्रिभुज ABC के शीर्ष A और B पर समान आवेश q रखे हैं। बिन्दु C पर विद्युत् क्षेत्र का परिमाण होगा :
View Solutionद्रव्यमान m एवं आवेश q का एक आवेशित कण स्थिर अवस्था से विद्युत् क्षेत्र E में छोड़ा जाता है। समय t के उपरान्त इसकी गतिज ऊर्जा होगी :
View Solutionदो समान आवेशों Q को मिलाने वाली रेखा के मध्य बिन्दु पर आवेश q रखा गया है। तीनों आवेशों का निकाय सन्तुलन में होगा, यदि
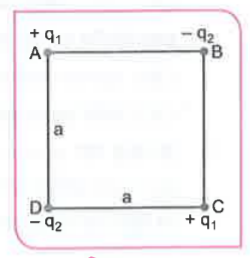
View Solutionसंलग्न चित्र 1.70 में भुजा a के वर्ग के कोनों पर आवेश स्थित हैं। यदि कोने A पर आवेश साम्य में है तो `(q_(1))/(q_(2))` का मान है :
View Solutionएक वर्ग के दो विपरीत कोनों पर आवेश Q रखा है तथा शेष दो कोनों पर आवेश q रखा है। यदि आवेश Q पर नैट विद्युत् बल शून्य है तो Q/q का मान है :
View Solutionदो बिन्दु आवेश + Q तथा- 2Q, X-अक्ष पर मूलबिन्दु से दूरी क्रमशः a तथा 2a पर स्थित हैं। परिणामी विद्युत् क्षेत्र की तीव्रता शून्य होगी :
View Solutionचित्र 1.71 में एक पतली अर्द्धवृत्तीय रिंग जिसकी त्रिज्या r है, पर धनात्मक आवेश एकसमान रूप से वितरित है। केन्द्र O पर परिणामी विद्युत् क्षेत्र `vecE` होगा :

View Solutionएक विद्युत् द्विध्रुव से दूरी r पर स्थित बिन्दु पर विद्युत् क्षेत्र अनुक्रमानुपाती होता है :
View Solutionएक विद्युत् द्विध्रुव जिसका द्विध्रुव आघूर्ण p है, के कारण निरक्षीय स्थिति में दूरी d पर विद्युत् क्षेत्र की तीव्रता होती है,
View Solutionएक विद्युत् द्विध्रुव जिसका द्विध्रुव आघूर्ण p है, की अक्षीय स्थिति में द्विश्रुव के केन्द्र से दूरी d पर विद्युत् क्षेत्र की तीव्रता होगी :
View Solutionविद्युत् द्विध्रुव की निरक्षीय रेखा पर स्थित बिन्दु पर विद्युत् क्षेत्र की दिशा अपने द्विध्रुव आघूर्ण की दिशा के :
View Solutionमूलबिन्दु O पर X-अक्ष के अनुदिश एक विद्युत् द्विध्रुव रखा गया है इस मूल बिन्दु से 20 सेमी दूर एक ऐसा बिन्दु P स्थित है कि रेखा OP, X-अक्ष से कोण `(pi)//3` बनाती है। यदि बिन्दु P पर विद्युत् क्षेत्र, X-अक्ष के साथ कोण `theta` बनाता है, तो `theta` का मान होगा :
View Solutionविद्युत् द्विध्रुव आघूर्ण p और 64 p वाले दो द्विध्रुवों को एक रेखा पर विपरीत दिशा में एक-दूसरे से 25 सेमी दूरी पर रखा गया है। दोनों द्विधरुवों के बीच में द्विध्रुव आघूर्ण p वाले द्विध्रुव से एक बिन्दु जहाँ विद्युत् क्षेत्र का मान शून्य है, की दूरी होगी :
View Solutionएक विद्युत् द्विध्रुव को `2xx 10^(5)` N/C तीव्रता के विद्युत् क्षेत्र से 30° कोण पर रखने से उस पर 4 N m का बल-आघूर्ण लगता है। यदि द्विध्रुव की लम्बाई 2 सेमी हो, तो उस पर आवेश होगा :
View Solutionएक विद्युत् द्विध्रुव का स्थिर आघूर्ण `vecP` है, जो कि X-अक्ष से `theta`-कोण बनाता है। विद्युत् क्षेत्र `vec(E_(1) = Ehati` में रखने पर यह बल आघूर्ण `vec(T_(1) = tauhatk` का अनुभव करता है। विद्युत क्षेत्र `vec(E_(2)) =sqrt3E_(1)hatj` में रखने पर यह बल आघूर्ण `vec(T_(2)) = - vec(T_(1))` का अनुभव करता है। कोण `theta` का मान होगा-
View Solutionएक विद्युत् द्विध्रुव जिसका आघूर्ण p है, को एक विद्युत् क्षेत्र E में क्षेत्र की दिशा से कोण `theta` घुमाने में किया गया कार्य होगा :
View Solutionएक विद्युत् द्विध्रुव एक बिन्दु आवेश से उत्पन्न विद्युत् क्षेत्र में किसी कोण पर रखा जाता है। द्विध्रुव पर आरोपित होगाः
View Solutionकिसी असमान विद्युत् क्षेत्र में विद्युत् क्षेत्र से कोण 30° बनाता एक विद्युत् द्विध्रुव रखा है। द्विध्रुव अनुभव करेगा :
View Solutionकिसी लम्बे बेलनाकार कोश के ऊपरी भाग में धनात्मक पृष्ठ आवेश घनत्व `sigma` तथा निचले भाग में त्रणात्मक पृष्ठ आवेश घनत्व `-sigma` है। बेलन के चारों ओर विद्युत् क्षेत्र-रेखाएँ होंगी :
View Solutionएक वैद्युत द्विध्रुव को एकसमान विद्युत क्षेत्र में रखा जाता है। द्विध्रुव पर कितना बल लगेगा?
View Solutionदूरी 2.4 Å पर रखे दो आवेश `+ 3.2xx10^(-19)C` तथा `-3.2xx 10^(-19)`C एक विद्युत् द्विध्रुव बनाते हैं। यदि इसे एकसमान तीव्रता वाले विद्युत् क्षेत्र `4xx10^(5)` वोल्ट/मीटर में रखा जाता है तो सन्तुलन में उसकी विद्युत् ऊर्जा होगी :
View Solutionमुक्त आकाश में आवेश वितरण क्षेत्र में स्थैत विद्युत् के लिए गॉस नियम का कथन है :
View Solutionएक घन के अन्दर आठ विद्युत् द्विध्रुव, जिनमें प्रत्येक के आवेश का परिमाण e है, रखे हैं। घन से निकलने वाला सम्पूर्ण विद्युत् फ्लक्स होगा :
View Solutionवायु में स्थित एकांक धन आवेश से निकलने वाले सम्पूर्ण विद्युत् फ्लक्स का मान है :
View Solutionएक घनीय बॉक्स के केन्द्र पर आवेश + Q स्थित है। बॉक्स की किसी एक दीवार से बाहर निकलने वाले सम्पूर्ण विद्युत् फ्लक्स का मान होगा :
View Solutionचित्र 1.73 में आवेश + Q घन के एक किनारे पर स्थित है। इस आवेश के कारण घन से विद्युत् फ्लक्स है :

View Solutionधारिता C के एक संधारित्र को विभव V से आवेशित किया जाता है। संधारित्र को परिबद्ध करने वाली बन्द पृष्ठ से विद्युत् क्षेत्र का फ्लक्स होगा :
View Solution1 मिमी त्रिज्या वाले एक लम्बे, सीधे तार पर विद्यत आवेश समान रूप से वितरित है तार की 1 सेमी लम्बाई पर आवेश Q कूलाम है। एक अन्य बेलनाकार पृष्ठ जिसकी त्रिज्या 50 सेमी तथा लम्बाई 1 मीटर है, इस तार को समान (सममित) रूप से घेरे है (चित्र 1.74)। इस बेलनाकार पृष्ठ से गुजरने वाले कुल विद्युत् फ्लक्स का मान होगा :

View Solutionएक घन जिसकी प्रत्येक भुजा x है, के केन्द्र से ठीक ऊपर x/2 दरी पर एक बिन्दु आवेश q रखा है। घन से सम्बद्ध विद्युत् फ्लक्स होगा :
View Solutionगॉस के नियम के सम्बन्ध में सत्य कथन है :
View Solutionगुरुत्वीय क्षेत्र के लिए गॉस के नियम के अनुसार :
View Solutionयदि किसी बन्द पृष्ठ में निवेशी व निर्गत विद्युत् फ्लक्स का मान न्यूटन मीट`र^(2)//`कूलॉम मात्रक में क्रमशः `8xx10^(3)` और `4xx10^(3)` है, तो पृष्ठ के अन्दर कुल आवेश है :
View Solutionत्रिज्या R के एकसमान आवेशित (कुल आवेश = Q) कुचालक गोले के कारण विद्युत् क्षेत्र E का गोले के केन्द्र से दूरी r के साथ विचरण का ग्राफ होगा :
View Solutionत्रिज्या R के किसी पतले गोलीय खोल के पृष्ठ पर आवेश Q एकसमान रूप से फैला है। इस खाल द्वारा `0lerltoo` परास में विद्युत् क्षेत्र E (r) का दूरी r के साथ परिवर्तन प्रदर्शित करने वाला ग्राफ है :
View Solutionत्रिज्या R के एक ठोस गोले पर कुल आवेश Q का आवेश घनत्व वितरण `p_((r))=(Qr)/(piR^(4))` है। गोले के अन्दर केन्द्र से दूरी `r_(1)` पर स्थित बिन्दु P पर विद्युत् क्षेत्र की तीव्रता होगी :
View Solutionएक गोलीय सममित आवेश वितरण में आवेश घनत्व का वितरण `p(r) = p_(0)(5/4-r/R),` जबकि r= R तथा `p_(r) = 0` जबकि rgt R है। यहाँ r केन्द्र से दूरी है। केन्द्र से दूरी r पर (rlt R) विद्युत् क्षेत्र की तीव्रता होगी :
View Solutionएक आवेश q के कारण दूरी R पर विद्युत् क्षेत्र E है। यदि इस आवेश को त्रिज्या R के ताँबे के गोले पर रख दिया जाए तो गोले की सतह पर विद्युत् क्षेत्र का मान होगा :
View Solutionएक विलगित धातु के ठोस गोले को आवेश + Q दिया जाता है। यह आवेश गोले पर वितरित होगा :
View Solutionप्रति लम्बाई आवेश q वाली अनन्त लम्बाई की नली में उसकी अक्ष से दूरी r पर विद्युत् क्षेत्र की तीव्रता होती है:
View Solutionएक ठोस धात्वीय गोले पर आवेश + 3Q है। इस गोले से संकेन्द्रीय एक चालक गोलीय कोश है जिस पर आवेश -Q है। गोले की त्रिज्या a तथा गोलीय कोश की त्रिज्या b (b gt a) है। केन्द्र से दूरी R (a gt R lt b) पर विद्युत् क्षेत्र है:
View Solutionकिसी सपाट वृत्तीय चकती पर आवेश + Q एकसमान वितरित है। आवेश + q को गतिज ऊर्जा E से, चकती की ओर, चकती के लम्बवत् अक्ष के मार्ग पर फेंका जाता है। आवेश q :
View Solutionएकसमान पृष्ठ आवेश धनत्व `sigma` वाले चालक पृष्ठ के निकट विद्युत क्षेत्र होता है :
View Solutionदो बड़ी धातु की प्लेटों को एक-दूसरे के समान्तर रखा जाता है। प्लेटों की आन्तरिक सतहों पर पृष्ठ आवेश घनत्व क़्रमशः `+sigma` तथा `-sigma` कूलॉम/मीट`र^(2)` है। प्लेटी के मध्य तथा प्लेटों के बाहर विद्युत क्षेत्र होगा :
View Solutionविद्युत् का चालक है :
View Solutionदो अनन्त लम्बाई के समान्तर तार, जिन पर आवेश का रखाये घनत्व क्रमशः `lamda_(1)` तथा `lamda_(2)` है, एक-दूसरे से R मीटर दरी पर रखे हैं। प्रत्येक तार की एकांक लम्बाई पर लगने वाला बल होगा :
View Solutionदो बराबर ऋणात्मक आवेश -q क्रमशः (0, a) तथा (0, - a) बिन्दुओं पर Y-अक्ष पर स्थित हैं। एक धनात्मक आवेश + Q को (2a, 0) बिन्दु से विरामावस्था से छोड़ा जाता है। आवेश + Q करेगा :
View Solutionदो अनन्त समतल और समान्तर कुचालक चादरों के बीच की दूरी d है। उन पर बराबर एवं विपरीत आवेश का पृष्ठ घनत्व `sigma` है। चादरों के बीच में किसी बिन्दु पर विद्युत् क्षेत्र की तीव्रता होगी :
View Solutionएक ही प्रकार के विद्युत् आवेशों से आवेशित तथा समान पृष्ठ आवेश घनत्व `sigma` वाले दो समान्तर पृष्ठों के बीच किसी बिन्दु पर विद्युत् क्षेत्र की तीव्रता होती है :
View Solutionयदि एक स्थिर-विद्युत् क्षेत्र में विद्युत् क्षेत्र की तीव्रता E हो तो विद्युत् ऊर्जा घनत्व अनुक्रमानुपाती होगा :
View Solutionकिसी चालक को दिया गया आवेश उसकी बाह्य सतह पर स्थित होता है क्योंकि :
View Solutionगुहायुक्त एक चालक को धनावेशित किया जाता है। यदि गुहा के अंदर बिन्दु A पर विद्युत् क्षेत्र E, गुहा के बाहर लोकिन चालक के अन्दर बिन्दु B पर विद्युत् क्षेत्र `E_(B)` तथा चालक के बाहर बिन्दु C पर विद्युत् क्षेत्र `E_(c)` है तो :
View Solutionपरावैद्युतांक K के माध्यम में विद्युत् क्षेत्र `vecE`है। यदि निर्वात की विद्युतशीलता `epsilon_(0)` है तो विद्युत् विस्थापन वेक्टर `vecD` है
View Solution
वस्तुनिष्ठ प्रश्न questions and complete solutions for chapter विद्युत् आवेश तथा क्षेत्र of SHIVALAL AGARWAL AND CO PHYSICS (HINDI) of Class 12
All Exercises from SHIVLAAL PUBLICATION Class 12 PHYSICS विद्युत् आवेश तथा क्षेत्र
- अभ्यास ( अति लघु उत्तरीय प्रश्न )
- अभ्यास ( एक शब्द/वाक्य में उत्तर दीजिए )
- अभ्यास ( प्रत्येक प्रश्न में दिए गए विकल्पों में से सही विकल्प चुनिए )
- अभ्यास ( बताइए की निम्न कथ्य सत्य है या असत्य )
- अभ्यास ( रिक्त स्थानों की पूर्ति कीजिए )
- अभ्यास ( लघु उत्तरीय प्रश्न )
- अभ्यास ( सही जोडिया बनाइए- )
- अभ्यास ( निबंधात्मक प्रश्न )
- आंकिक उदाहरण
- आंकिक प्रश्न
- तथ्यात्मक प्रश्न
- बोधात्मक प्रश्न
- वस्तुनिष्ठ प्रश्न
- संख्यात्मक प्रश्न