Complete Solutions to Problems of chapter ELECTROSTATIC FORCES, CHARGES AND FIELDS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROSTATIC FORCES, CHARGES AND FIELDS |
| SL ARORA | Problems |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
Five point charges, each of value +q are placed on five vertices of a regular hexagon of side Lm. What is the magnitude of the force on a point charge of value -q coulomb placed at the centre of the hexagon?
View SolutionFour particles each having a charge q, are placed on the four vertices of a regular pentagon. The distance of each corner from the centre is a. Find the electric field at the centre of the pentagon.
View SolutionA charges Q is placed at each of the two opposite corners of a square. A charge q is placed to each of the other two corners. If the resultant force on each charge q is zero, then
View SolutionTwo similarly and equally charged identical metal spheres A and B repel each other with a force of `2xx10^(-5)N`. A third identical uncharged sphere C is touched with A and then placed at the midpoint between A and B. Find the net electric force on C.
View SolutionA copper ball of density `8.6 g cm^(-3)` and 1 cm in diameter is immersed in oil of density `0.8 g cm^(-3)`. What is the charge on the ball, if it remains just suspended in oil in electric field of intensity `3600 V//m` acting in the upward direction ?
View SolutionA charged particle of radius `5xx10^(-7)m` is located in a horizontal electric field of intensity `6.28xx10^(5)Vm^(-1)`. The surrounding medium has the coefficient of viscosity `eta=1.6xx10^(5)Nsm^(-2)`. The particle starts moving under the effect of electric field and finally attains a uniform horizontal speed of `0.02 ms^(-1)`. Find the number of electrons on it. Assume gravity free space.
View SolutionTwo identical charged spheres are suspended by strings of equal lengths. The strings make an angle of `30^@` with each other. When suspended in a liquid of density `0.8gcm^-3`, the angle remains the same. If density of the material of the sphere is `1.6gcm^-3`, the dielectric constant of the liquid is
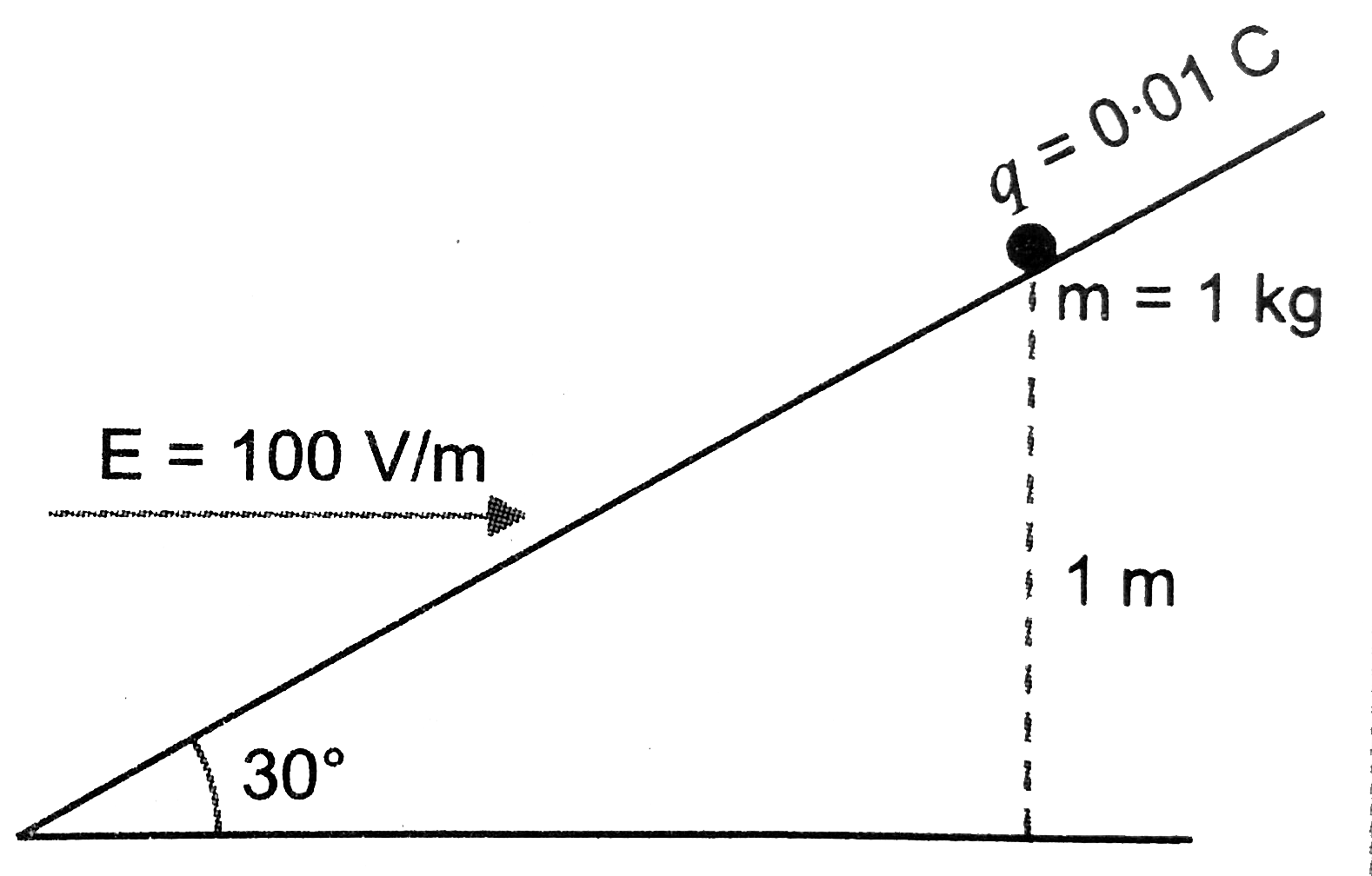
View SolutionAn inclinded plane making an angle of `30^(@)` with the horizontal electric field of `100 Vm^(-1)` as shown in Figure. A particle of mass `1 kg` and charge `0*01 C` is allowed to slide down from rest from a height of `1m`. If the coefficient of friction is `0.2`, find time taken by the particle to reach the bottom.
View SolutionTwo point charges+ q and-q are placed at distanced apart. What are the points at which the resultant field is parallel to the line joining the two charges ?
View SolutionThree particles, each of mass m and carrying a charge q each, are suspended from a common point by insulating mass-less strings each of length L. If the particles are in equilibrium and are located at the corners of an equilateral triangle of side a, calculate the charge q on each particle. Assume `Lgtgta`.
View SolutionA ball of mass `10^(-2) kg` and having charge `+ 3 xx 10^(-6)C` is tied at one end of a `1m` along thread. The other end of the thread is fixed and a charge `- 3 xx 10^(-6) C` is placed at this end. The ball can move in the circulr orbit of radius `1m` in the vertical plane. Initially, the ball is at the bottom. Find the monimum initial horizontal velocity of the ball, so that it will be able to complete the full circle.
View SolutionA charge ` + 10^-9 C` is located at the origin in free space `&` another charge ` Q` at ` (2,0,0)` . If the X-component of the electric field at (3,1,1) is zero , calculate the value of `Q`, Is the Y-component zero at (3,1,1) ?
View SolutionConsider the classical model of an electron such that a nucleus of charge +e is uniformly distributed within a sphere of radius`2Å`. An electron of charge -e at a radial distance `1Å` moves inside this sphere. Find the force a!tracting the electron on to the centre of the sphere. Calculate the frequency with which the electron would oscillate about the centre of the sphere, if released from rest at this radial distance.
View SolutionA uniform electric field of intensity `E = 10^(6) V//m` exist in vertically downwards direction in a region. A particle of mass m = 0.01 kg andcharge `q= 10^(-6) C` is suspended byan inextensible thread oflength `I= 1m`. The particle is displaced slightly from its mean position and released. Calculate the time period ofits oscillation. What minimum velocity should be given to the particle at rest from its equilibrium position so that it completes a full circle in vertical plane? Calculate the maximum and minimum tension in the thread in its circular motion in vertical plane. `[0.6s, 23.42 m//s, 6.59 N,0]`
View SolutionA point particle of mass M is attached to one end of a massless rigid non-conducting rod of length L. Another point particle of the same mass is attached to the other end of the rod. The two particles carry charges `+q` and `-q` respectively. This arrangement is held in a region of a uniform electric field E such that the rod makes a small angle `theta` (say of about 5 degree) with the field direction, fig. Find an expression for the minimum time needed for the rod to become parrallel to the field after it is set free.

View SolutionA charge of `4xx10^(-9)C` is distributed uniformly over the circumference of a conducting ring of radius 0.3m. Calculate the field intensity at a point on the axis of the ring at 0.4m from its centre, and also at the centre.
View SolutionA ring of radius 0.1m is made out of thin metallic wire of area of cross section `10^(-6)m^(2)`. The ring has a uniform charge of `pi` coulombs. Find the change in the radius of the rig when a charge of `10^(-8)C` is placed at the center of the ring. Young's modulus of the metal is `2xx10^(11)Nm^(-2)`.
View SolutionTwo charges, each equal to q, aer kept at `x=-a` and `x=a` on the x-axis. A particle of mass m and charge `q_0=q/2` is placed at the origin. If charge `q_0` is given a small displacement (ylt lt a) along the y-axis, the net force acting on the particle is proportional to
View Solution
Problems questions and complete solutions for chapter ELECTROSTATIC FORCES, CHARGES AND FIELDS of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 12