Complete Solutions to Problems From Competitive Examinations of chapter MAGNETISM of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MAGNETISM |
| SL ARORA | Problems From Competitive Examinations |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
Two identical magnetic dipoles of magnetic moments `1*0Am^2` each are placed at a separation of `2m` with their axes perpendicular to each other. What is the resultant magnetic field at a point midway between the dipoles?
View SolutionA bar magnetic with poles `25cm` apart and pole strength `14*4A.m` rests with its centre on a frictionless pivot. It is held in equilibrium at `60^@` to a uniform magnetic field of induction `0*25T` by applying a force F at right angles to its axis, `10cm` from the pivot. Calculate the value of F. What will happen if the force is removed?
View SolutionA bar magnet of length 2 l and magnetic moment m is suspended freely in a uniform magnet field B. Find the amount of work done to deflect the magnet through an angle `theta` from the direction of the field.
View SolutionA small magnet of magnetic moment M is placed at broad side on position of a magnet of magnetic M', length 2l' in such a way that the axis of former coincides with the perpendicular bisector of the latter. The separation between their centres is d. Calculate the nature of interaction (force or couple ) among them. What is its limiting value, when d becomes very large ?
View SolutionA small coil of radius 0.002 m is placed on the axis of a magnet of magnetic moment `10^(5)` `JT^(-1)` and length 0.1 m at a distance of 0.15 m from the centre of the magnet. The plane of the coil is perpendicular to the axis of the magnet. Find the force on the when a current of 2.0 A is passed through it.
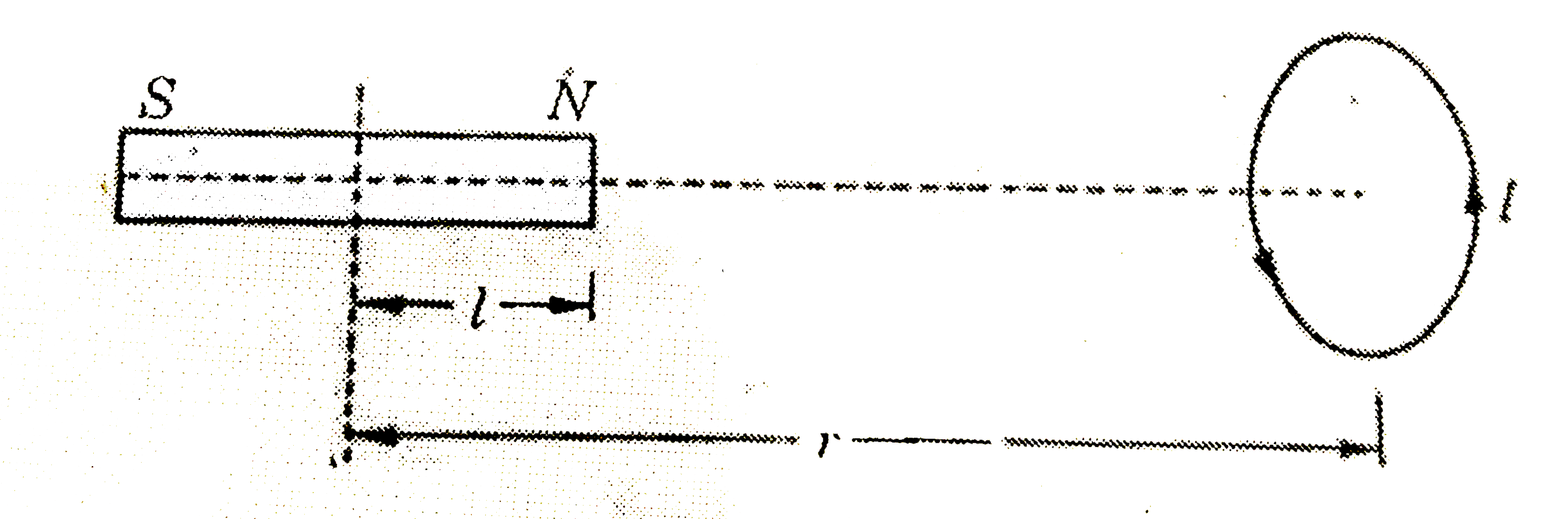
View SolutionA magnet is suspended in the magnetic meridian with an untwisted wire. The upper end of wire is rotated through `180^(@)` to deflect the magnet by `30^(@)` from magnetic meridian. When this magnet is replaced by another magnet, the upper end of wire is rotated through `270^(@)` to deflect the magnet `30^(@)` from magnetic meridian. The ratio of magnetic moment of magnets is
View SolutionA small magnet of magnetic moment `pixx10^(-3) Am^(2)` is placed on the Y-axis at a distance of 0.1 from the origin with its axis parallel to the X-axix. A coil have 169 turns and radius 0.05 m is placed on the X-axis at a distance of 0.12 m from the origin with the axis of the coil coinciding with the X-axis. Find the magnitude and direction of the current in the coil for a compass needle placed at the origin, to point in the north-south direction.
View SolutionA circular of radius 0.157 m has turns. It is placed such that its axis is in magnetic meridian. A dip needle is supported at the centre of the coil with its axis of rotation horizontal, and in the plane of the coil. The angle of dip is `30^(@)` when a current flows through the coil. The angle of dip becomes `60^(@)` on reversing the current. Find the current in the coil assuming that the magnetic field due to the coil is smaller than the horizontal component of earth's magnetic field, `H =3xx10^(-5) T`.
View SolutionTwo circular coils, each of 100 turns, are held that one lies in the vertical plane and the other in the horizontal plane with their centres coinciding. The radii of the vertical and the horizontal coils are respectively 20 cm and 30 cm. If the directions of the currents in them are such that the earth's magnetic field at the centre of the coils is exactly neutralised, then calculate the current in each coil. (Horizontal component of earth's magnetic field`=27.8 Am^(-1)`, angle of dip`=30^(@)`
View SolutionA compass needle whose magnetic moment is `60Am^2` pointing geograhic north at a certain place, where the horizontal component of earth's magnetic field is `40muWbm^-2` experiences a torque `1*2xx10^-3Nm`. What is the declination of the place?
View SolutionThe periodic times of oscillation of a dip needle in two perpendicular vertical planes are `t_(1)` and `t_(2)` respectively. If the periodic time of the same needle in the magnetic meridian is t, showthat
`(1)/(t_(1)^(4))+(1)/(t_(2)^(4))=(1)/(t_(4))(1+sin^(2)delta )`
where `delta` is the angle of dip.
View SolutionThe period of oscillation of a suspended thin cylindrical magnet is 4 seconds. It is broken into exactly two halves. Find the period of oscillation of each half when freely suspended.
View SolutionA vibration magnetometer consists of two identical bar magnets placed one over the other, such that they are mutually perpendicular and bisect each other The time period of oscillation in horizontal magnetic field is 4 s. If one the magnets is taken away, find the period of oscillation of the other in the same field.
View Solution
Problems From Competitive Examinations questions and complete solutions for chapter MAGNETISM of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 12