Complete Solutions to Example of chapter TRANSIENT CURRENT of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | TRANSIENT CURRENT |
| SL ARORA | Example |
| Number Of Questions | 37 |
| Academic Year | 2023-24 |
A narrow uniform glass tube 80 cm long and open at both ends is half immersed in mercurry. Then the top of the tube is closed and it is taken out of mercury. A column of mercury 22 cm long then remains in the tube. What is the atmospheric pressure?
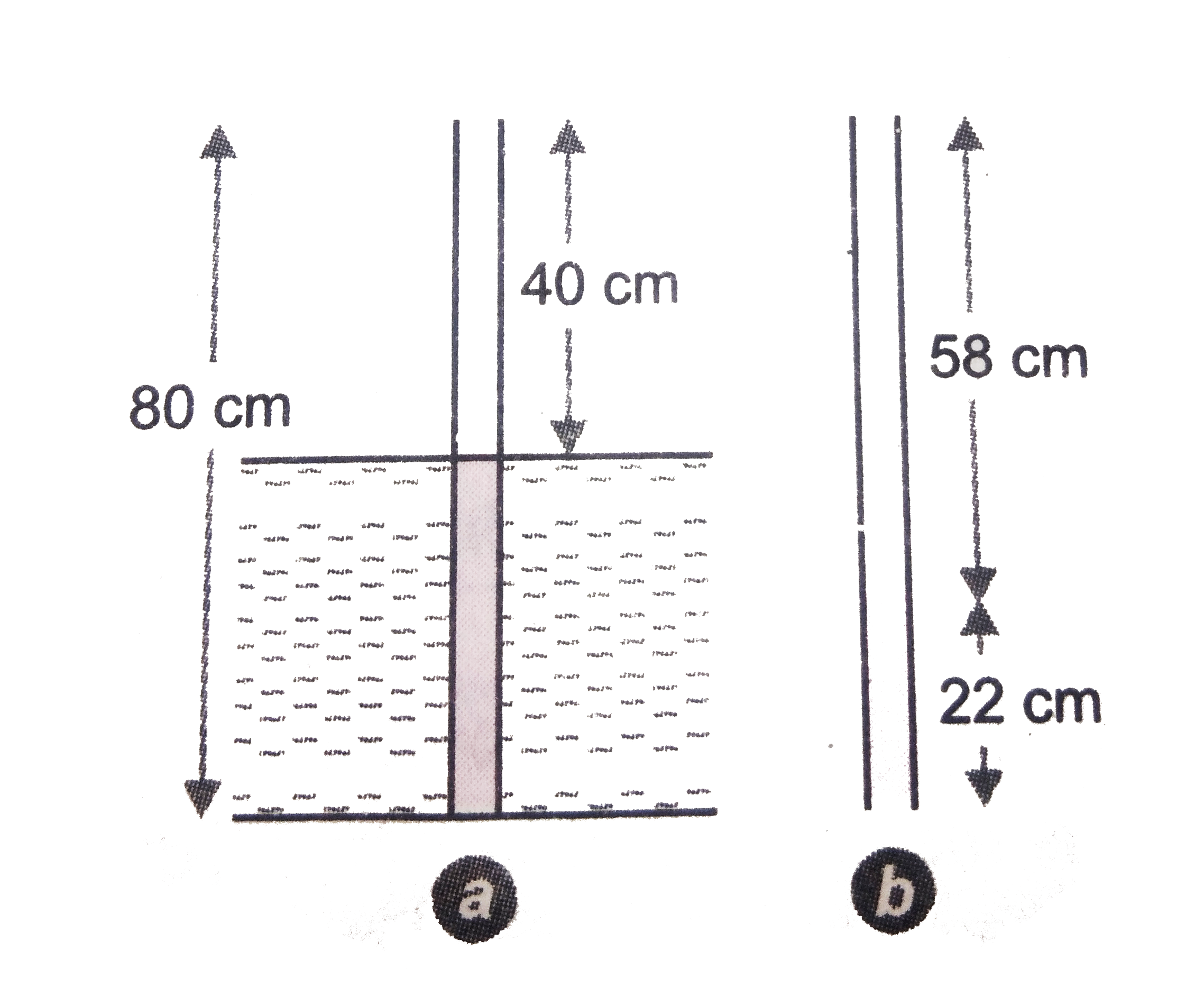
View SolutionA metre long narrow bore held horizontally (and close at one end) contains a `76` cm long mercury thread, which traps a `15` cm column of air. What happens if the tube is held vertically with the open end at the bottom?
View SolutionA given mass of a gas at `-73^(@)C` exerts a pressure of `50` cm of mercury. What pressure will it exert at `27^(@)C`, if the volume remains constant?
View SolutionThe rms velocity of hydrogen at S.T.P is `u` `ms^(-1)`. If the gas is heated at constant pressure till its volume is three fold, what will be its final temperature and rms velocity ?
View SolutionA gas at `27^@ C` in a cylinder has a volume of 4 litre and pressure `100 Nm^-2`.
(i) Gas is first compressed at constant temperature so that the pressure is `150 Nm^-2` . Calculate the change in volume.
(ii) It is then heated at constant volume so that temperature becomes `127^@ C`. Calculate the new pressure.
View SolutionAs an air bubble rises from the bottom of a lake to the surface, its volume is doubled. Find the depth of the lake. Take atmospheric pressure = 76 cm of Hg.
View SolutionMolar volume is the volume occupied by 1 mole of any (Ideal) gas at standard temperature and pressure (STP , `0^(@) C`, 1 atmospheric pressure). Show that it is 22.4 litres. Take `R = 8.31 J mol^(-1) K^(-1)`.
View SolutionUsing the ideal gas equation, determine the value of gas constant R. Given that one gram mole of a gas at S.T.P occupies a volume of 22.4 litres
View SolutionMolecular weight of oxygen is `32`. At S.T.P., volume of `1 g` of oxygen is `700 cm^(3)`. Find the value of gas constant R.
View SolutionEstimate the total number of air molecules (inclusive of oxygen, nitrogen, water vapour and other constituents) in a room of capacity `25.0 m^(3)` at a temperature of `27^(@) C` and 1 atm pressure. (Boltzmann constant `= 1.38 xx 10^(-23) JK^(-1))`.
View SolutionAn air bubble of volume `1.0 cm^(3)` rises from the bottom of a lake 40 m deep at a temperature of `12^(@) C`. To what volume does it grow when it reaches the surface, which is at a temperature of `35^(@) C`. ? Given `1 atm = 1.01 xx 10^(5) Pa`.
View SolutionAn oxygen cylinder of volume 30 litres has an initial gauge pressure of 15 atm. And a temperature of `27^(@)C`. After some oxygen is withdrawn from the cylinder, the gauge pressure drops to 11 atm. And its temperature drops to `17^(@)C`. Estimate the mass of oxygen taken out of the cylinder. `(R = 8.1 J "mole"^(-1) K^(-1)`, molecular mass of `O_(2) = 32 u)`.
View SolutionA mixture of hydrogen and oxygen has volume `2000cm^(3)`, temperature `300K`, pressure `100KPa` and mass `0.76g`.Calculate the masses of hydrogen and oxygen in the mixture.
View SolutionA vessel with open mouth contains air at `60^@C`. When the vessel is heated upto temperature T, one fourth of the air goes out. The value of T is
View SolutionThe density of nitrotgen is `1.25 kgm^(-3)` at S.T.P. Find its density at `42^(@)C` and `730 mm` of Hg.
View SolutionA vessel contains `14g` of hydrogen and `96g` of oxygen at STP.
(a) Find the volume of the vessel.
(b) Chemical reaction is induced by passing electric spark in the vessel till one of the gases is consumed, The temperature is brought back to its starting value `273K`. Find the pressure in the vessel.
View SolutionA vessel contains two non-reactive gases neon (monoatomic) and oxygen (diatomic). The ratio of their partial pressures is 3:2. Estimate the ratio of
(i) number of molecules, and
(ii) mass density of neon and oxygen in the vessel.
Atomic mass of neon = 20.2 u, and molecular mass of oxygen = 32.0 u.
View SolutionFour molecules of a gas have speeds `2, 4, 6` and `8 kms^(-1)` respectively. Calculate their average speed and root mean square speed.
View SolutionIf three gas molecules have velocity `0.5`, `1` and `2 km//s` respectively, find the ratio of their root mean square speed and average speed.
View SolutionCalculate the r.m.s. velocity of air molecules at `S.T.P.` Given density of air at `S.T.P.` is `1.296 kg m^(-3)`.
View SolutionCalculate the rms velocity of oxygen molecules at S.T.P. The molecular weight of oxygen is 32.
View SolutionCalculate the temperature at which the rms speed of nitrogen molecules will be equal to `8 km//s`. Given molecular weight of nitrogen = 28 and `R = 8.31 J/mole/K.
View SolutionThe r.m.s speed of oxygen molecule `(O_(2))` at a certain temperature T is V. If on increasing the temperature of the oxygen gas to 2T, the oxygen molecules dissociate into atomic oxygen, find the speed of the oxygen atom.
View SolutionCalculate the temperature at which r.m.s velocity of gas molecules is double its value at `27^(@)C`, pressure of the gas remaining the same.
View SolutionCalculate the temperature at which rms velocity of a gas is half its value at `0^(@)C`, pressure remaining constant
View SolutionAt what temperature is the root mean square speed of an atom in an argon gas cylinder equal to the r.m.s. speed of a helium gas atom at `-20^(@) C` ? (Atomic mass of Ar = 39.9 u, of He = 4.0 u).
View SolutionA vessel is filled with a gas at a pressure of 76 cm of mercury at a certain temperature. The mass of the gas is increased by 50% by introducing more gas in the vessel at the same temperature. Find the resultant pressure of the gas.
View SolutionEstimate the average energy of a helium atom at (i) room temperature `(27^(@)C)` (ii) the temperature on the surface of the sun `(6000 K)` and (iii) the temperature of `10^(7)K`. Given `k_(B) = 1.38 xx 10^(-23) J "molecule"^(-1) K^(-1)`
View SolutionCalculate the kinetic energy of one mole of argon at `127^(@)C`. Given,Boltzmann's constant, `k_(B) = 1.381 xx 10^(-23) J "molecular"^(-1) K^(-1)`. Avogardro numbe, `N = 6.02 xx 10^(23) "mol"^(-1)`
View SolutionCalculate the kinetic energy of `1` gram of helium `(M = 4)` at `127^(@)C`. Given `R = 8.31 J "mole"^(-1) K^(-1)`.
View SolutionThe kinetic energy of a molecule of oxygen at `0^(@)C` is `5.64 xx 10^(-21) J`. Calculate Avogadro's number. Given `R = 8.31 J "mol^(-1)K^(-1)`.
View SolutionCalculate the kinetic energy of one gram mole of gas at NTP. Density of gas `= 0.178 kg m^(-3)` at NTP. Its molecular weight = 4. Density of mercury `= 13.6 xx 10^(3) kg m^(-3)`.
View SolutionCalculate the KE per molecule and also rms velocity of a gas at `127^(@)C`. Given `k = 1.38 xx 10^(-23) J "molecule"^(-1) K^(-1)` and mass of each molecule `= 6.4 xx 10^(-27) kg`.
View Solution(a) Calculate (i) root-mean-square speed and (ii) the mean energy of 1 mol of hyderogen at STP given that density of hydrogen is `0.09 kg//m^(3)`. (b) Given that the mass of a molecule of hydergen is `3.34 xx 10^(-27)` kg, calculate Avogadro's number. (c ) Calculate Boltmann's constant.
View SolutionAt what temperature will the average velocity of oxygen molecules be sufficient to escape from the earth. Given mass of oxygen molecule `= 5.34 xx 10^(-26) kg`. Boltzmann constant, `k = 1.38 xx 10^(-23) J "molecule"^(-1) K^(-1)`. Escape velocity of earth `= 11.0 km s^(-1)`.
View SolutionCalculate the temperature at which the average K.E. of a molecule of a gas will be the same as that of an electron accelerated through 1 volt. Boltzmann constant `= 1.4 xx 10^(-23) J "molecule"^(-1) K^(-1)`, charge of an electron `= 1.6 xx 10^(-19)C`.
View SolutionA vessel A contains hydrogen and another vessel B whose volume is twice that of A contains same mass of oxygen at same temperature. Compare
(i) average KE of hydrogen and oxygen molecule.
(ii) root mean square speeds of molecules
(iii) pressure of gases in A and B.
Molecular weight of hydrogen and oxygen are 2 and 32 respectively.
View Solution
Example questions and complete solutions for chapter TRANSIENT CURRENT of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 12