Complete Solutions to PART B of chapter ANNUAL EXAMINATION QUESTION PAPER JUN-2019 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | ANNUAL EXAMINATION QUESTION PAPER JUN-2019 |
| SUBHASH PUBLICATION | PART B |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
Find gof and fog given `f(x) = 8x^(3) and g(x) = x^(1//3)`.
View SolutionProve the following:
`"tan"^(-1)2/11+"tan"^(-1)7/14="tan"^(-1)1/2`
View SolutionWrite `cot^(-1)(1/(sqrt(x^(2)-1))),xgt1`, in the simplest form.
View SolutionFind the area of the triangle with vertices, (3,8), (-4,2) and (5,1) using determinants.
View SolutionFind `(dy)/(dx)` given `x^(2) + xy + y^(2) = 100`.
View SolutionDifferentiate `(log_(e)x)cos x` with respect to x.
View SolutionFind the interval in which the function f given by `f(x)=2x^(2)-3x` is strictly increasing.
View SolutionFind `int ((x^(4)-x)^(1/4))/(x^(5)) dx`.
View SolutionIntegrate `x sec^(2)x `with respect to x.
View SolutionFind the order and degree (if defined) of the differential equation:
`y^(' ' ')+y^(2)+e^(y')=0`.
View SolutionIf `veca` is a unit vector and `(vecx-veca). (vecx+veca)=8`, then find `|vex|`.
View SolutionFind the area of the parallelogram whose adjacent sides are given by the vectors `veca=3hati+hatj+4hatk and b=hati-hatj+hatk`.
View SolutionFind the angle between the pair of lines `(x+3)/(3)=(y-1)/(5)=(z+3)/(4) and (x+1)/(1)=(y-4)/(1)=(z-5)/(2)`
View SolutionThe probability distribution of random variable X is as follows:
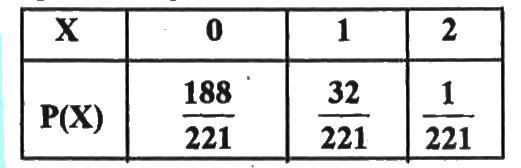 . Find expectation of X.
. Find expectation of X.
View Solution
PART B questions and complete solutions for chapter ANNUAL EXAMINATION QUESTION PAPER JUN-2019 of JEEVITH PUBLICATIONS MATHS (KANNADA ENGLISH) of Class 12