Complete Solutions to EXERCISE of chapter ANNUAL EXAMINATION QUESTION PAPER JUNE-2019 (WITH ANSWERS) of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | ANNUAL EXAMINATION QUESTION PAPER JUNE-2019 (WITH ANSWERS) |
| SUBHASH PUBLICATION | EXERCISE |
| Number Of Questions | 38 |
| Academic Year | 2023-24 |
Write the formula to find the sum of first n terms of an Arithmetic progression, whose first term is a and the last term is `a_n`.
View SolutionIf a pair of linear equations represented by lines has no solutions (inconsistent) then write what kinds of lines are these.
View SolutionWrite the formula to find area of a sector of a circle, if angle at the centre is `'theta'` degrees.
View SolutionWrite 96 as the product of prime factors.
View SolutionFind the degree of the polynomial
`P(x)=x^3+2x^2-5x-6`
View SolutionIna `Delta ABC, angle ABC=90^@ and angle ACB=30^@` then find `AB:AC`.
View SolutionFind the solution for the pair of linear equations:
`x+y=14`
`x-y=4`
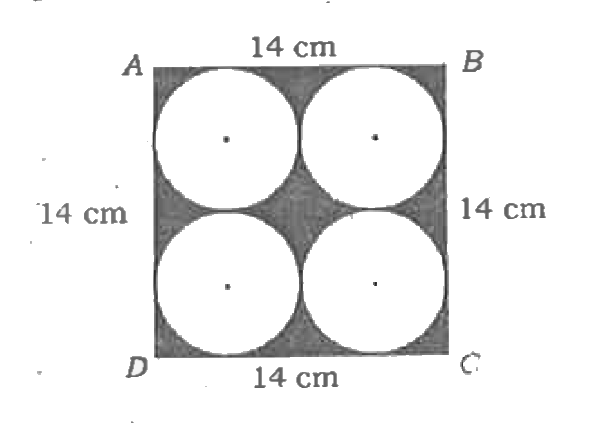
View SolutionABCD is a square of side 14cm. Four congruent circles are drawn in the square as shown in figure. Calculate the area of the shaded region.
[ Circles touch each other externally and also sides of the square]
View SolutionFind the distance between the points `(2,3) and (4,1)`.
View SolutionFind the area of a triangle whose vertices are `(1,-1),(-4,6) and (-3,-5)`.
View SolutionProve that `5+sqrt3` is an irrational number.
View Solution`Delta ABC~Delta DEF` and their areas are `64 cm^2 and 100 cm^2` respectively. If `EF=12 cm` then find the measure of BC.
View SolutionA verticle pole of height 6m casts a shadow 4m long on the ground, and at the same time a tower on the same ground casts a shadow 28m long. Find the height of the tower.
View SolutionThe diagonal BD of parallelogram ABCD intersect AE at F as shown in the figure. If E is any point on BC, then prove that `DFxxEF=FB=FA`.
View Solutionsum and product of the zeroes of a quadratic polynomial `P(x)=ax^2+bx-4 "are" 1/4 and -1` respectively. Then find the values of a and b.
View SolutionFind the quotient and remainder when `p(x)=2x^2+2x+1` is divided by `g(x)=x+2`
View SolutionFind the value of k, in which one of its zeros is `-4` of the polynomial `P(x)=x^2-x-(2k+2)`.
View SolutionSolve the equation `x^2-3x-10=0` by using formula.
View SolutionIf `cosec theta=(13)/(12)` then find the value of `cos theta`.
View Solution`tan A . Sin A+ cos A=secA`
View SolutionDraw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of `60^(@)`.
View SolutionA box contains 90 discs. Which are numbered from 1 to 90. If one disc is drawn at randow from the box. Find the probability that is bears a perfect square number.
View SolutionA metallic sphere of radius 9cm is melted and recast into the shape of a cyclinder of radius 6 cm. Find the height of the cyclinder.
View SolutionThe faces of two cubes of volume `125 cm^3` each are joined together to form a cuboid. Find the total surface area of the cuboid.
View SolutionProve that the "Length of tangents drawn from an external point a circle are equal".
View SolutionTwo concentric circle of radii 5 cm and 3cm are drawn. Find the length of the chord of the larger circle which touches the smaller circles.
View SolutionConstruct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are `(7)/(5)` of the corresponding sides of the first triangle.
View SolutionFind the mode for the following data in the frequency distribution table:
View SolutionFind the median for the following data in the frequency distribution table:

View SolutionFrom the of a vertical building of `50sqrt3 m ` height on a level ground the angle of depression of an object on the same ground is observed to be `60^@`. Find the distance of the object from the foot of the building.
View SolutionTwo windmills of height 50m and `40sqrt3 m` are on either side of the field. A person observes the top of the windmills from a point in between them. The angle of elevation was found to be `45^@ and 30^@`. Find the distance between the windmills.

View SolutionThe following table gives production yield per hectare of wheat of 100 farms of a village.
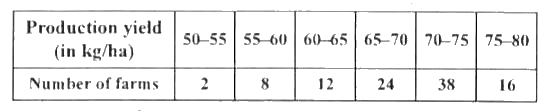
Change the distribution, and draw its ogive
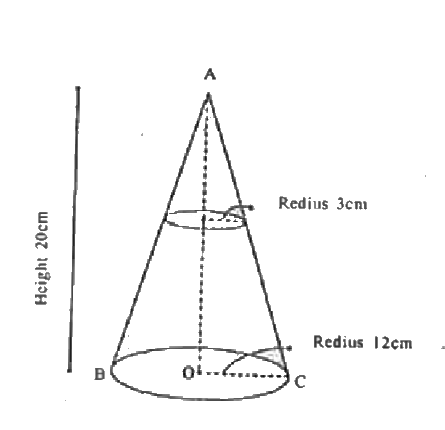
View SolutionA cone is having its base radius 12 cm and height 20 cm. If the top of this cone is cut in to form of a small cone of base radius 3cm is remove, then the remaining part of the solid cone becomes a frustum. Calculate the volume of the frustum.
View SolutionThe sum o the fourth and eighth terms of arithmetic progression is 24 and the sum of the sixth and tenth terms is 44. Find the first three terms of the Arithmetic progression:
View SolutionProve that "In a right triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides".
View SolutionSolve graphically
`2x+y=8`
`x-y=1`
View SolutionThe ages of two students A and B are 19 years and 15 years respectively. Find how many years it will take so that the product of their ages becomes equal to 480.
View SolutionIf the quadratic equation `(b-c)x_2+(c-a)x+(a-b)=0` has equal roots, then show that `2b=a+c`.
View Solution
EXERCISE questions and complete solutions for chapter ANNUAL EXAMINATION QUESTION PAPER JUNE-2019 (WITH ANSWERS) of JEEVITH PUBLICATIONS MATHS (KANNADA ENGLISH) of Class 12