Complete Solutions to PART - D of chapter II PUC MATHEMATICS ANNUAL EXAM QUESTION PAPER MARCH - 2020 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | II PUC MATHEMATICS ANNUAL EXAM QUESTION PAPER MARCH - 2020 |
| SUNSTAR PUBLICATION | PART - D |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
If `f:RrarrR` defined by `f(x)=(4x+3)`, show that f is invertible and find`f^(-1`.
05:02View SolutionIf `A=[(1,2,-3),(5,0,2),(1,-1,1)],B=[(3,-1,2),(4,2,5),(2,0,3)]andC=[(4,1,2),(0,3,2),(1,-2,3)]` then compute (A + B) and (B - C). Also verify that A + (B - C) = (A + B) - C.
05:42View SolutionSolve system of linear equations , using matrix method
` 2x+ 3y + 3z=5`
` x-2y +z=-4`
` 3x-y-2z=3`11:50View SolutionIf `y=(tan^(-1)x)^(2)`, show that
`(x^(2)+1)^(2)y_(2)+2x(x^(2)+1)y_(1)=2`.04:35View SolutionSand is pouting from a pipe at the rate of `12cm^(3)//s`. The falling sand forms a cone on the ground in such a way that the height of the cone is always one - sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm ?
06:11View SolutionFind the integral of `1/(x^(2)+a^(2))` w.r.t x and hence evaluate `int1/(x^(2)+2x+2)dx`.
06:43View SolutionUsing the method of integration, find the area of the smaller region bounded by the ellipse `x^(2)/9+y^(2)/4=1` and the line `x/3+y/2=1`.
10:06View SolutionFind the general solution of the differential equation `xdy/dx+2y=x^(2)logx`.
06:00View SolutionDerive the equation of a line in space passing through a given point and parallel to a given vector in both Vector an Cartesian form.
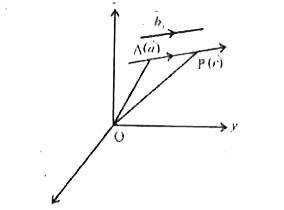 06:35View Solution
06:35View SolutionA person buys a lottery ticket in 50 lotteries, in ech of which his chance of winning a prize is 1/100. What is the probability that he will a prize (a) exactly once (b) atleast once ?
06:34View Solution
PART - D questions and complete solutions for chapter II PUC MATHEMATICS ANNUAL EXAM QUESTION PAPER MARCH - 2020 of SUNSTAR MATHS (KANNADA ENGLISH) of Class 12
