Complete Solutions to EXERCISE of chapter இரு பரிமாண பகுமுறை வடிவியல் - II of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | இரு பரிமாண பகுமுறை வடிவியல் - II |
| SURA PUBLICATION(TAMIL) | EXERCISE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
ஆரம் 5 செ.மீ. அலகுகள் படையதும், x-அச்சை ஆதிப்புள்ளியில் தொட்டுச் செல்வதுமான வட்டத்தின் சமன்பாட்டைத் தருவிக்க.
04:56View Solution(2, -1) என்ற புள்ளியை மையமாகவும், (3, 6) என்ற புள்ளி வழிச் செல்வதுமான வட்டத்தின் சமன்பாடு காண்க.
03:26View Solutionஇரு அச்சுக்களையும் தொட்டுச் செல்வதும், (-4 -2) என்ற புள்ளி வழிச் செல்வதுமான வட்டத்தின் சமன்பாடு காண்க.
06:49View Solutionமையம் (2, 3) உடையதும் 3x-2y-1=0 மற்றும் 4x+y-27=0 என்ற கோடுகள் வெட்டும் புள்ளி வழி செல்வதுமான வட்டத்தின் சமன்பாடு காண்க.
07:01View Solution(3, 4) மற்றும் (2, -7) என்ற புள்ளிகளை விட்டத்தின் முனைப்புள்ளிகளாகக் கொண்ட வட்டத்தின் பயன்பாட்டைப் பெறுக.
03:03View Solution(1, 0), (-1, 0) மற்றும் (0,1) என்ற புள்ளிகள் வழிச்செல்லும் வட்டத்தின் சமன்பாடு காண்க.
04:21View Solution`9pi` சதுர அலகுகள் பரப்பு கொண்ட வட்டத்தின் விட்டங்கள், x+y=5 மற்றும் x-y=1 என்ற நேர்கோடுகள் மீது அமைந்துள்ளன எனில் அந்த வட்டத்தின் சமன்பாடு காண்க.
03:56View Solution`y=2sqrt2x+c` என்ற கோடு `x^2+y^2=16` என்ற வட்டத்தின் தொடுகோடு எனில், c-என் மதிப்பு காண்க.
03:14View Solution`x^2+y^2-6x+6y-8=0` என்ற வட்டத்தின் தொடுகோடு மற்றும் செங்கோட்டுச் சமன்பாடுகளை (2,2) என்ற புள்ளியில் காண்க.
04:23View Solution(-2, 1), (0, 0) மற்றும் (-4, -3) என்ற புள்ளிகள் `x^2+y^2-5x+2y-5=0` என்ற வட்டத்திற்கு வெளியே, வட்டத்தின் மீது அல்லது உள்ளே இவற்றில் எங்கே உள்ளன எனத் தீர்மானிக்கவும்.
04:30View Solutionபின்வரும் வட்டங்களுக்கு மையத்தையும் ஆரத்தையும் காண்க. `x^2+(y+2)^2=0`
02:30View Solutionபின்வரும் வட்டங்களுக்கு மையத்தையும் ஆரத்தையும் காண்க. `x^2+y^2+6x-4y+4=0`
02:49View Solutionபின்வரும் வட்டங்களுக்கு மையத்தையும் ஆரத்தையும் காண்க. `x^2+y^2-x+2y-3=0`
03:05View Solutionபின்வரும் வட்டங்களுக்கு மையத்தையும் ஆரத்தையும் காண்க. `2x^2+2y^2-6x+4y+2=0`
03:02View Solution`3x^2+(3-p)xy+qy^2-2px=8pq` என்ற சமன்பாடு வட்டத்தைக் குறிக்கும் எனில் p மற்றும் q-ன் மதிப்பு காண்க. மேலும் அந்த வட்டத்தின் மையம் மற்றும் ஆரம் காண்க.
04:24View Solutionபின்வரும் ஒவ்வொன்றிற்கும் பரவளையத்தின் சமன்பாடு காண்க: குவியம் (4, 0) மற்றும் இயக்குவரை x=-4.
03:22View Solutionபின்வரும் ஒவ்வொன்றிற்கும் பரவளையத்தின் சமன்பாடு காண்க: y-அச்சுக்கு சமச்சீரானது மற்றும் (2, -3) வழிச்செல்வது.
02:01View Solutionபின்வரும் ஒவ்வொன்றிற்கும் பரவளையத்தின் சமன்பாடு காண்க: முனை (1,-2) மற்றும் குவியம் (4, -2).
03:52View Solutionபின்வரும் ஒவ்வொன்றிற்கும் பரவளையத்தின் சமன்பாடு காண்க: செவ்வகலத்தின் முனைன் (4, -8) மற்றும் (4,8).
01:46View Solutionபின்வரும் ஒவ்வொன்றிற்குமான நீள்வட்டத்தின் சமன்பாடு காண்க : குவியங்கள் (± 3, 0), மற்றும் `e=frac{1}{2}`
03:30View Solutionபின்வரும் ஒவ்வொன்றிற்குமான நீள்வட்டத்தின் சமன்பாடு காண்க : குவியங்கள் (0, ± 4) மற்றும் நெட்டச்சின் முனைகள் (0, ± 5).
03:54View Solutionபின்வரும் ஒவ்வொன்றிற்குமான நீள்வட்டத்தின் சமன்பாடு காண்க : செவ்வகல நீளம் 8, `e=frac{3}{5}` மற்றும் நெட்டச் x-அச்சு.
05:11View Solutionபின்வரும் ஒவ்வொன்றிற்குமான நீள்வட்டத்தின் சமன்பாடு காண்க :செவ்வகல நீளம் 4, குவியங்களுக் கிடையேயான தூரம் `4sqrt2` மற்றும் y-அச்சு.
04:32View Solutionபின்வரும் ஒவ்வொன்றிற்குமான அதிபர வளையத்தின் சமன்பாடு காண்க: குவியங்கள் (± 2, 0), `e=frac{3}{2}`.
04:21View Solutionபின்வரும் ஒவ்வொன்றிற்குமான அதிபர வளையத்தின் சமன்பாடு காண்க: மையம் (2,1), ஒரு குவியம் (8,1) மற்றும் இதற்கொத்த இயக்குவரை x= 4.
06:03View Solutionபின்வரும் ஒவ்வொன்றிற்குமான அதிபர வளையத்தின் சமன்பாடு காண்க: (5, -2) வழிச்செல்வது மற்றும் குற்றச்சின் நீளம் 8 அலகுகள், நெட்டச்சு x அச்சு.
04:00View Solutionபின்வருவனவற்றிற்கான முனை, குவியம், இயக்கவரையின் சமன்பாடு மற்றும் செவ்வகல நீளம் காண்க. `y^2=16x`
02:12View Solutionபின்வருவனவற்றிற்கான முனை, குவியம், இயக்கவரையின் சமன்பாடு மற்றும் செவ்வகல நீளம் காண்க. `x^2=24y`
03:01View Solutionபின்வருவனவற்றிற்கான முனை, குவியம், இயக்கவரையின் சமன்பாடு மற்றும் செவ்வகல நீளம் காண்க. `y^2=16x`
02:12View Solutionபின்வருவனவற்றிற்கான முனை, குவியம், இயக்கவரையின் சமன்பாடு மற்றும் செவ்வகல நீளம் காண்க. `x^2-2x+8y+17=0`
06:33View Solutionபின்வருவனவற்றிற்கான முனை, குவியம், இயக்கவரையின் சமன்பாடு மற்றும் செவ்வகல நீளம் காண்க. `y^2-4y-8x+12=0`
04:44View Solutionபின்வரும் சமன்பாடுகளின் கூம்பு வளைவின் வகையைக் கண்டறிந்து அவற்றின் மையம், குவியங்கள், முனைகள் மற்றும் இயக்குவரைகள் காண்க. `frac{x^2}{25}+frac{y^2}{9}=1`
04:34View Solutionபின்வரும் சமன்பாடுகளின் கூம்பு வளைவின் வகையைக் கண்டறிந்து அவற்றின் மையம், குவியங்கள், முனைகள் மற்றும் இயக்குவரைகள் காண்க. `frac{x^2}{3}+frac{y^2}{10}=1`
05:31View Solutionபின்வரும் சமன்பாடுகளின் கூம்பு வளைவின் வகையைக் கண்டறிந்து அவற்றின் மையம், குவியங்கள், முனைகள் மற்றும் இயக்குவரைகள் காண்க. `frac{x^2}{25}-frac{y^2}{144}=1`
03:58View Solutionபின்வரும் சமன்பாடுகளின் கூம்பு வளைவின் வகையைக் கண்டறிந்து அவற்றின் மையம், குவியங்கள், முனைகள் மற்றும் இயக்குவரைகள் காண்க. `frac{y^2}{16}-frac{x^2}{9}=1`
03:05View Solution`frac{x^2}{a^2}-frac{y^2}{b^2}=1` என்ற அதிபரவளையத்தின் செவ்வகல நீளம் `frac{2b^2}{a}` என நிறுவுக.
04:25View Solutionஅதிபரவளையத்தின் மீதுள்ளள்ள புள்ளி P-இலிருந்து அதன் குவியத்தூரங்களின் வித்தியாசத்தில் மட்டு மதிப்பு குறுக்கச்சின் நீளத்திற்குச் சமம் என நிறுவுக.
05:49View Solutionபின்வரும் சமன்பாடுகளின் கூம்பு வளைவின் வகையைக் கண்டறிந்து அவற்றின் மையம், குவியங்கள், முனைகள் மற்றும இயக்குவரைகளைக் காண்க: `frac{(x-3)^2}{225}+frac{(y-4)^2}{289}=1`
09:10View Solutionபின்வரும் சமன்பாடுகளின் கூம்பு வளைவின் வகையைக் கண்டறிந்து அவற்றின் மையம், குவியங்கள், முனைகள் மற்றும இயக்குவரைகளைக் காண்க:`frac{(x+1)^2}{100}+frac{(y-2)^2}{64}=1`
08:05View Solutionபின்வரும் சமன்பாடுகளின் கூம்பு வளைவின் வகையைக் கண்டறிந்து அவற்றின் மையம், குவியங்கள், முனைகள் மற்றும இயக்குவரைகளைக் காண்க: `frac{(x+3)^2}{225}-frac{(y-4)^2}{64}=1`
06:29View Solutionபின்வரும் சமன்பாடுகளின் கூம்பு வளைவின் வகையைக் கண்டறிந்து அவற்றின் மையம், குவியங்கள், முனைகள் மற்றும இயக்குவரைகளைக் காண்க: `frac{(y-2)^2}{25}-frac{(x+1)^2}{16}=1`
06:24View Solutionபின்வரும் சமன்பாடுகளின் கூம்பு வளைவின் வகையைக் கண்டறிந்து அவற்றின் மையம், குவியங்கள், முனைகள் மற்றும இயக்குவரைகளைக் காண்க: `18x^2+12y^2-144x+48y+120=0`
09:37View Solutionபின்வரும் சமன்பாடுகளின் கூம்பு வளைவின் வகையைக் கண்டறிந்து அவற்றின் மையம், குவியங்கள், முனைகள் மற்றும இயக்குவரைகளைக் காண்க: `9x^2-y^2-36x-6y+18=0`
08:26View Solutionபின்வரும் சமன்பாடுகளிலிருந்து அவற்றின் கூம்பு வளைவு வகையை கண்டறிக. `2x^2-y^2=7`
02:03View Solutionபின்வரும் சமன்பாடுகளிலிருந்து அவற்றின் கூம்பு வளைவு வகையை கண்டறிக. `3x^2+3y^2-4x+3y+10=0`
02:47View Solutionபின்வரும் சமன்பாடுகளிலிருந்து அவற்றின் கூம்பு வளைவு வகையை கண்டறிக. `3x^2+2y^2=14`
03:27View Solutionபின்வரும் சமன்பாடுகளிலிருந்து அவற்றின் கூம்பு வளைவு வகையை கண்டறிக. `x^2+y^2+x-y=0`
03:46View Solutionபின்வரும் சமன்பாடுகளிலிருந்து அவற்றின் கூம்பு வளைவு வகையை கண்டறிக. `11x^2-25y^2-44x+50y-256=0`
02:38View Solutionபின்வரும் சமன்பாடுகளிலிருந்து அவற்றின் கூம்பு வளைவு வகையை கண்டறிக. `y^2+4x+3y+4=0`
02:03View Solution(5,2) என்ற புள்ளியிலிருந்து `2x^2+7y^2=14` என்ற நீள்வட்டத்திற்கு வரையப்படும் தொடு கோடுகளின் சமன்பாடுகளைக் காண்க.
07:09View Solution`frac{x^2}{16}-frac{y^2}{64}=1` என்ற அதிபரவளையத்திற்கு, 10x-3y+9=0 என்ற நோக்கோட்டிற்கு இணையான தொடுகோட்டுச் சமன்பாடுகளைக் காண்க.
04:42View Solutionx-y+4=0 என்ற நேர்க்கோடு `x^2+3y^2=12` என்ற நீள்வட்டத்தின் தொடுகோடு என நிறுவுக மேலும் தொடும் புள்ளியைக் காண்க.
04:51View Solution`y^2=16x` என்ற பரவளையத்திற்கு 2x+2y+3=0 என்ற கோட்டிற்குச் செங்குத்தான தொடு கோட்டுச் சமன்பாடு காண்க.
03:38View Solution`y^2=8x` என்ற பரவளையத்திற்கு t = 2 இல் தொடு கோட்டுச் சமன்பாடு காண்க, (குறிப்பு துணையலகு வடிவத்தைப் பயன்படுத்துக)
03:10View Solution`12x^2-9y^2=108` என்ற அதிபரவளையத்திற்கு `theta=frac{pi}{3}` இல் தொடுகோடு மற்றும் செங்கோட்டுச் சமன்பாடுகளைக் காண்க.
06:16View Solution`y^2=4ax` என்ற பரவளையத்திற்கு `'t_1'`மற்றும் `'t_2'` ஆகிய புள்ளிகளில் அமையும் தொடுகோடுகள் `[a`'t_1'` `'t_2'`, 'a(t_1+t_2)']என்ற புள்ளியில் சந்திக்கின்றன என நிறுவுக.
04:09View Solution`y^2=4ax` என்ற பரவளையத்திற்கு `'t_1'` என்ற புள்ளியில் வரையப்படும் செங்கோடு, பரவளையத்தை மீண்டும் `'t_2'` என்ற புள்ளியில் சந்திக்குமெனில், `t_2=-(t_1+frac{2}{t_1})` என நிறுவுக.
04:53View Solutionஒரு பாலம் பரவளைய வளைவில் உள்ளது மையத்தில் 10மீ உயரமும், அடிப்பகுதியில் 30மீ அகலமும் உள்ளது. மையத்திலிருந்து இருபுறமும் 6 மீ தூரத்தில் பாலத்தின் உயரத்தைக் காண்க.
06:05View Solutionஒரு நான்கு வழிச்சாலைக்கான மலையழியே செல்லும் சுரங்கப்பாதையின் முகப்பு ஒரு நீள்வட்டவடிவமாக உள்ளது. நெடுஞ்சாலையின் மொத்த அகலம் (முகப்பு அல்ல) 16மீ. சாலையின் விளிம்பில் சுரங்கப்பாதையின் உயரம், 4மீ உயரமுள்ள சரக்கு வாகனம் செல்வதற்குத் தேவையான அளவிற்கும் முகப்பின் அதிகபட்ச உயரம் 5மீ ஆகவும் இருக்க வேண்டுமெனில் சுரங்கப்பாதையின் திறப்பின் அகலம் என்னவாக இருக்க வேண்டும்?
06:00View Solutionஒரு நீருற்றில், ஆதியிலிருந்து 0.5மீ கிடைமட்டத் தூரத்தில் நீரின் அதிகபட்ச உயரம் 4மீ, நீரின் பாதை ஒரு பரவளையம் எனில் ஆதியிலிருந்து 0.75மீ கிடைமட்டத் தூரத்தில் நீரின் உயரத்தைக் காண்க.
09:09View Solutionபொறியாளர் ஒருவர் குறுக்கு வெட்டு பரவளையமாக உள்ள ஒரு துணைக்கோள் ஏற்பியை வடிவமைக்கின்றார். ஏற்பி அதன் மேல்பக்கத்தில் 5மீ அகலமும், முனையிலிருந்து குவியம் 1.2 மீ தூரத்திலும் உள்ளது. முனையை ஆதியாகவும், x-அச்சு பரவளையத்தின் சமச்சீர் அச்சாகவும் கொண்டு ஆய அச்சுகளைப் பொகுத்தி பரவளையத்தின் சமன்பாடு காண்க.
03:25View Solutionபொறியாளர் ஒருவர் குறுக்கு வெட்டு பரவளையமாக உள்ள ஒரு துணைக்கோள் ஏற்பியை வடிவமைக்கின்றார். ஏற்பி அதன் மேல்பக்கத்தில் 5மீ அகலமும், முனையிலிருந்து குவியம் 1.2 மீ தூரத்திலும் உள்ளது. முனையிலிருந்து செயற்கைக்கோள் ஏற்பியின் ஆழம் காண்க.
05:45View Solutionஒரு தொங்கு பாலத்தின் 60மீ சாலைப்பகுதிக்கு பரவளைய கம்பி வடம் படத்தில் உள்ளவாறு பொறுத்தப்பட்டுள்ளது. செங்குத்துக் கம்பி வடங்கள் சாலைப் பகுதியில் ஒவ்வொன்றுக்கும் 6மீ இடைவெளி இருக்குமாறு அமைக்கப் பட்டுள்ளது. முனையிலிருந்து முதல் இரண்டு செங்குத்து கம்பி வடங்களுக்கான நீளத்தைக் காண்க.
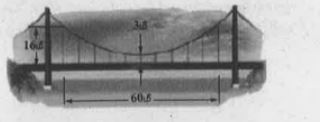 10:10View Solution
10:10View Solutionஒரு அணு உலை குளிரூட்டும் தூணின் குறுக்கு வெட்டு அதிபரவளையவடிவில் உள்ளது. மேலும் அதன் சமன்பாடு `frac{x^2}{30^2}-frac{y^2}{44^2}=1` தூண் 150மீ உயரமுடையது. மேலும் அதிபரவளையத்தின் மையத்திலிருந்து தூணின் மேல்பகுதிக்கான தூரம் மையத்திலிருந்து அடிப்பகுதிக்கு உள்ள தூரத்தில் பாதியாக உள்ளது. தூணின் மேற்பகுதி மற்றும் அடிப்பகுதியின் விட்டங்களைக் காண்க.
 05:59View Solution
05:59View Solution1.2 மீ நீளமுள்ள தடி அதன் முனைகள் எப்போதும் ஆய அச்சுகளைத் தொட்டுச் செல்லுமாறு நகருகின்றது. தடியின் x-அச்சு முனையிலிருந்து 0.3மீ தூரத்தில் உள்ள ஒரு புள்ளி P-ன் நியமப்பாதை ஒரு நீள்வட்டம் என நிறுவுக, மேலும் அதன் மையத்தொலைத்தகவும் காண்க.
06:46View Solutionதரைமட்டத்திலிருந்து 7.5மீ உயரத்தில் தரைக்கு இணையாகப் பொருத்தப்பட்ட ஒரு குழாயிலிருந்து வெளியேறும் நீர் தரையைத் தொடும் பாதை ஒரு பரவளையத்தை ஏற்படுத்துகிறது, மேலும் இந்தப் பரவளையப் பாதையின் முனை குழாயின் வாயில் அமைகிறது. குழாய் மட்டத்திற்கு 2.5மீ கழே நீரின் பாய்வானது குழாயின் முனை வழியாகச் செல்லும் நிலை குத்துக்கோட்டிற்கு 3மீ தூரத்தில் உள்ளது எனில் குத்துக் கோட்டிலிருந்து எவ்வளவு தூரத்திற்கு அப்பால் நீரானது தரையில் விழும் என்பதைக் காண்க.
06:47View Solutionஒரு ராக்கெட் வெடியானது கொளுத்தும்போது அது ஒரு பரவளையப் பாதையில் செல்கிறது அதன் உச்ச உயரம் 4 மீ -ஐ எட்டும் போது அது கொளுத்தப்பட்ட இடத்திலிருந்து கிடைமட்டத் தூரம் 6மீ தொலைவிலுள்ளது. இறுதியாக கிடைமட்டமாக 12மீ தொலைவில் தரையை வந்தடைகிறது. எனில் புறப்பட்ட இடத்தில் தரையுடன் ஏற்படுத்தப்படும் எறிகோணம் காண்க.
07:22View SolutionA, B என்ற இரு புள்ளிகள் 10கி.மீ இடைவெளியில் உள்ளன. இந்தப் புள்ளிகளில் வெவ்வேறு நேரங்களில் கேட்கப்பட்ட வெடிச்சத்தத்திலிருந்து வெடிச்சத்தம் உண்டான இடம் A என்ற புள்ளி B என்ற புள்ளியைவிட 6 கி.மீ அருகாமையில் உள்ளது என நிர்ணயிக்கப்பட்டது வெடிச்சத்தம் உண்டான இடம் ஒரு குறிப்பிட்ட வளைவரைக்கு உட்பட்டது என நிரூபித்து அதன் சமன்பாட்டைக் காண்க
08:53View Solution(1, 5) மற்றும் (4,1) என்ற புள்ளிகள் வழிச் செல்வதும் y-அச்சைத் தொட்டுச் செல்வதுமான வட்டத்தின் சமன்பாடு `x^2+y^2-5x-6y+9+lambda(4x+3y=19)=0`எனில், `lambda` -ன் மதிப்பு
View Solutionசெவ்வகல நீளம் 8 அலகுகள் மற்றும் துணையச்சின் நீளம் குவியங்களுக்கிடையே உள்ள தூரத்தில் பாதி உள்ள அதிபரவளையத்தின் மையத்தொலைத் தகவு
View Solutionவட்டம் `x^2+y^2=4x+8y+5` நேர்க்கோடு `3x-4y=m` -ஐ இரு வெவ்வேறு புள்ளிகளில் வெட்டுகின்றது எனில்
View Solutionx-அச்சு (1, 0), என்ற புள்ளியில் தட்டுச் செல்வதும் (2,3) என்ற புள்ளிவழிச் செல்வதுமான வட்டத்தின் விட்டம்
View Solution`3x^2+by^2+4bx-6by+b^2=0` என்ற வட்டத்தின் ஆரம்
03:08View Solution`x^2-8x-12=0` மற்றும் `y^2-14y+45=0` என்ற கோடுகளால் அடைபடும் சதுரத்தின் உள்ளே வரையப்படும் மிகப்பெரிய வட்டத்தின் ஆரம்
View Solutionநேர்க்கோடு 2x + 4y = 3 -க்கு இணையாக `x^2+y^2-2x 2y+1=0` என்ற வட்டத்தின் செங்கோட்டுச் சமன்பாடு
View SolutionP(x,y) என்ற புள்ளி குவியங்கள் F_1(3,0) மற்றும் F_2(-3,0) கொண்ட கூம்பு வளைவு `16x^2+25y^2=400` -ன் மீதுள்ள புள்ளி எனில் -ன் மதிப்பு
View Solutionx+y=6 மற்றும் x + 2y = 4 என்ற நேர்க்கோடுகளை விட்டங்களாகக் கொண்டு (6,2) புள்ளிவழிச் செல்லும் வட்டத்தின் ஆரம்
View Solution`frac{x^2}{a^2}-frac{y^2}{b^2}=1` மற்றும் `frac{x^2}{a^2}-frac{y^2}{b^2}=-1` என்ற அதிபர வளையங்களின் குவியங்கள் ஒரு நாற்கரத்தின் முனைகள் எனில் அந்த நாற்கரத்தின் பரப்பு
View Solution`y^2=4x` என்ற பரவளையத்திற்கும் அதன் செவ்வகலத்திற்கும் இடையே பரப்பானது
02:03View Solution`x + y = k` என்ற நேர்க்கோடு பரவளையம் `y^2 = 12x`-இன் செங்கோட்டுச் சமன்பாடாக உள்ளது எனில் k-ன் மதிப்பு
04:12View Solutionநீள்வட்டம் `E_1 : frac{x^2}{9}+frac{y^2}{4}=1` செவ்வகம் R-க்குள் செவ்வகத்தின் பக்கங்கள் நீள்வட்டத்தின் அச்சுகளுக்கு இணையாக இருக்குமாறு அமைந்துள்ளன. அந்த செவ்வகத்தின் சுற்று வட்டமாக அமைந்த மற்றொரு நீள்வட்டம் (0,4) என்ற புள்ளி வழியாகச் செல்கிறது எனில் அந்த நீள்வட்டத்தின் மையத்தொலைத் தகவு
View Solution2x-y=1 என்ற கோட்டிற்கு இணையாக `frac{x^2}{9}-frac{y^2}{4}=1` என்ற நீள்வட்டத்திற்கு தொடு கோடுகள் வரையப்பட்டால் தொடுபுள்ளிகளில் ஒன்று
View Solution`frac{x^2}{16}+frac{y^2}{9}=1` என்ற நீள்வட்டத்தின் குவியங்கள் வழியாகவும் (0,3) என்ற புள்ளியை மையமாகவும் கொண்ட நீள்வட்டத்தின் சமன்பாடு
View SolutionC என்ற வட்டத்தின் மையம் (1, 1) மற்றும் ஆரம் 1 அலகு என்க. T என்ற வட்டத்தின் மையம் (0,y) ஆகவும் ஆதிப்புள்ளி வழியாகவும் உள்ளது. மேலும் C என்ற வட்டத்தை வெளிப்புறமாகத் தொட்டுச் செல்கிறது எனில் வட்டம் -ன் ஆரம்
View Solutionமையம் ஆதிப்புள்ளியாகவும் நெட்டச்சு x-அச்சாகவும் உள்ள நீள்வட்டத்தைக் கருத்தில் கொள்க. அதன் மையத்தொலைத் தகவு `frac{3}{5}` மற்றும் குவியங்களுக்கிடையே உள்ள தூரம் 6 எனில் அந்த நீள்வட்டத்தின் உள்ளே நெட்டச்சு மற்றும் குற்றச்சுகளை மூலைவிட்டங்களாகக் கொண்டு வரையப்படும் நாற்கரத்தின் பரப்பு
View Solution`frac{x^2}{a^2}+frac{y^2}{b^2}=1` என்ற நீள்வட்டத்தினுள் வரையப்படும் மிகப்பெரிய செவ்வகத்தின் பரப்பு
View Solutionநீள்வட்டத்தின் அரைக்குற்றச் OB, F மற்றும் F' மற்றும் FBF' ஒரு செங்கோணம் எனில் அந்த நீள்வட்டத்தின் மையத்தொலைத் தகவு காண்க
View Solution`(x-3)^2+(y-4)^2=frac{y^2}{9}` என்ற நீள்வட்டத்தின் மையத்தொலைத் தகவு
View SolutionP என்ற புள்ளியிலிருந்து என்ற பரவளையத்திற்கு வரையப்படும் இரு தொடுகோடுகளுக்கிடையேயான கோணம் செங்கோணம் எனில் P-ன் நியமப்பாதை
View Solution(1, -2) என்ற புள்ளி வழியாகவும் (3,0) என்ற புள்ளியில் x-அச்சைத் தொட்டுச் செல்வதுமான வட்டம் பின்வரும் புள்ளிகளில் எந்தப் புள்ளி வழியாகச் செல்லும்?
View Solution(-2, 0) - இலிருந்து ஒரு நகரும் புள்ளிக்கான தூரம் அத்தப் புள்ளிக்கும் நேர்க்கோடு `x=frac{-9}{2}` -க்கும் இடையேயான தூரத்தைப் போல் `frac{2}{3}` மடங்கு உள்ளது எனில் அந்தப் புள்ளியின் நியமப்பாதை
View Solution`x^2+y^2-8x-4y+c=0` என்ற வட்டத்தின் விட்டத்தின் ஒரு முனை (11, 2) எனில் அதன் மறுமுனை
View Solution(0,4) மற்றும் (0, 2) என்பது பரவளையத்தின் முனை மற்றும் குவியம் எனில் அதனுடைய சமன்பாடு
View Solutionபரவளையம் `y^2 + 4y + 4x + 2 = 0` -ன் செவ்வகலத்தின் சமன்பாடு
View Solution(-4, 4) ல்`x^2=-4y` ன் தொடுகோட்டு சமன்பாடு
View Solution`y^2-2x-2y+5=0` என்பது ஒரு
View Solutionஒரு பரவளைய எதிரொளிப்பான் 20 செ.மீ. விட்டம் மற்றும் 5 செ.மீ ஆழமுடையது எனில் அதனுடைய குவியம்
View Solutionநீள்வட்டம் `9x^2+5y^2-30y=0` மையத் தொலைத் தகவு
View Solutionநீள்வட்டம் `frac{x^2}{36}+frac{y^2}{49}=1` செவ்வகத்தின் நீளம்
View Solutionகுவியங்களுக்கு இடைப்பட்ட தூரம் 2 மற்றும் 5, எனில் நீன்வட்டத்தின் சமன்பாடு
View Solution
EXERCISE questions and complete solutions for chapter இரு பரிமாண பகுமுறை வடிவியல் - II of SURA MATHS (TAMIL) of Class 12
