Complete Solutions to Mathematics of chapter AP EAMCET ENGINEERING ENTRANCE EXAM of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | AP EAMCET ENGINEERING ENTRANCE EXAM |
| TS EAMCET | Mathematics |
| Number Of Questions | 59 |
| Academic Year | 2023-24 |
if f:R `rarr` R is defined bty
`f(x)={{:(|[x-5]|, "for" x lt 5),([|x-5|],"for" x ge5):}`
Then (fof)`(-7/2)`=
(here [x] is the greatest integer not exceeding x)
View SolutionIf f:A `rarr` B is an on to function such that f(x)=`sqrt(|x|-x)+(1)/sqrt(|x|-x)` then A and B are respectively
View Solution`1/2.5+1/5.8+1/8.11+….16` terms =
View SolutionIf `f(x)=|(1+sin^(2)x,cos^(2)x,4sin2x),(sin^(2)x,1+cos^(2)x,4sin2x),(sin^(2)x,cos^(2)x,1+4sin2x)|` then the maximum value of `f(x)` is
View SolutionIf `A={:[(1,0,-2),(-2,-1,2),(3,4,1)]:}` then `A^(-1)` =
View SolutionIf the system of simultaneous linear equations x+y+z=a,x-y+bz=2, 2x+3y -z=1 has infinitely many solutions then b-5a=
View SolutionIf z=x +iy,x,y `in` R and if the point p in the agrand plane represents z then the locus of p satisfying the condition arg `(z-1)/(z-3i)=(pi)/(2)` is
View SolutionIf P,Q and R are points respectively representing the complex numbers z , `ze^(ipi/3)` and `z(1+e^(ipi/3))` in agrand plane then area of the triangle PQR is
View Solution`A(z_(1))` and `B(z_(2))` are two points in the argand plane then the locius of the complex number z satisfying arg `(z-z_(1))/(z-z_(2))=0` or `pi` is
View SolutionIf x is a cube root of unity other than 1 then `(x+(1)/(x))^(2)+[x^(2)+(1)/(x^(2))]^(2)+…+[(x^(12))+(1)/(x^(12))]^(2)=`
View SolutionIf `3x^(2)-7x+2=0` and `15x^(2)-11x+a=0` have a common root and a is a positive real number then the sum of the roots of the equation `15x^(2) -ax +7=0` is
View SolutionLet `alpha,beta` be the roots of the equation `x^(2)-|a|x-|b|=0` such that `|alpha|lt |beta|` if `|a|lt beta-1` then the positive root of `log_|alpha|[(x^(2))/(beta^(2))]-1=0` is
View SolutionIf x `in` R and `1 le ((3x^(2)-7x+8)/(x^(2)+1))le 2` then the minimum and maximum values of x are respectively
View SolutionLet `phi(x)=(x)/(x^(2)+1)(x+1)` if a, b and c are the roots of the equation `x^(3) -3x+lambda=0(lambda ne 0)` Then `phi(a)phi(b)phi(c )` =
View SolutionIn an examination hall there are 'mn' chairs in m rows and n columns the number of ways in which m students can be seated such that no row is vacant is
View SolutionConsider the folowing statements I:The number of non trivial even divisors of the number `2^(a_(1)),3^(a_(2)),4^(a_(3)),5^(a_(4)),6^(a_(3))` is
`a_(2)+a_(4)+a_(5)+a_(2)a_(4)+a_(4)a_(5)` Then
View SolutionThe coefficient of `x^(5)` in the expansion of `(x^(2)+2x+3)^(5)` is
View SolutionIf x is so small, that` x^5 `and higher power of x may be neglected, then the coefficient of `x^4 ` in the expansion of `[x^2+4]^(1/2)` -`(x^2+9)^(1/2)`
View SolutionIf `(8)/((x+3)^(2)(x-2))=(Ax+B)/(x+3)^(2)+(C )/(x-2)` then 25(B+8C-A)=
View SolutionLet `alpha,beta` and `gamma` be such that `0 lt alpha lt beta lt gamma lt 2pi` for any x `in` R if
`cos (x+alpha)+cos(x + beta)+cos(x+gamma)=0` then `tan(gamma-alpha)` =
View SolutionIf ABC is not a right andgled triangle and `sin((pi)/(4)-A)sin(pi)/(4-B)=-(1)(2sqrt(2))cosec ((pi)/(4)-C)`
then tan A tan B + tan B tan C + tan C tan A=
View SolutionIf tan `(theta)/(2) =cosec theta - sin theta` then `tan^(2)(theta/2)=`
View SolutionThe number of real values of
`x in [0,2pi]-{(pi)/(2),(3pi)/(2)}` satisfying the equation `|cos x|^[2sin^(2)x-3 sinx +1]`=1 is
View SolutionThe sum of the maximum and the minimum values of `2(cos^(-1)x)^(2)-pi cos^(-1) x+(pi^(2))/(4)` is
View SolutionIf y=`log_e` tan `((pi)/(4)+(x)/(2))` then tan h `(y)/(2)=`
View SolutionIn `triangle` ABC if a,b and c are in arithmetic progression then cos A + 2cosB + cosC=
View SolutionIf the area of triangle ABC is `b^(2) - (c - a)^(2) ` then tan B=
View Solution`(1)/(r^(2))+(1)/(r_(1)^(2))+(1)/(r_(2)^(2))+(1)/(r_(3)^(2))` equals
View SolutionFor a non zero real number x if the points with position vectors
`(x-u)hati+xhatj+xhatk,xhati+(x-v)hatj+xhatk,xhati+xhatj+(x-w)hatk` and `(x-1)hati+(x-1)hatj+(x-1)hatj` are coplanar then
View SolutionIf p is a point lying on the line passing throiugh the point `A(hat i-hatj +2hatk)` and parallel to the vector `2hat i+hatj =2hat k` such that |AP|=18 then a position vector of p is
View Solutiona,b,c are three vectors such that |a|=1,|b|=2,|c |=3 and b.c =0 if the projection of b along a is equal to projecton of c along a then |2a+3b-3c|=
View SolutionLet m be a vector of magnitude `sqrt(3)` and perpendicular to the vectors `hati+hatj` and `hatj-hatk` let n be another vector of magnitude `2sqrt(6)` and perpendicular to the vectors `2hat I -hatj` and `hat j+2 hatk` The area in sq units of the triangle fromed with m and n side is
View Solution`a = hat I -hatj +hat k b=hat I -2hat j +hat k ,c =phat I +2 hat j +q hatk` and `d=phat I + q hat j +2 hat k` are given vectors if the projection of c on a is `5sqrt(3)` units and if a,b and c form a parallelopiped of volume 5 cubic units then `tan^(-1)(b,d)=`
View SolutionGiven `a=2 hati +hat j +hat k, b =hati+2 hat j -hatk` and a unit vector c are coplanar if c is perpendicular to a , then c=
View SolutionThe coefficient of variation of 9,3,11,5,7 is
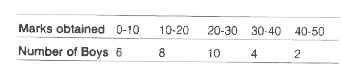
View SolutionThe mean deviation about the mean for the following data
View SolutionThe probability of occurrence of an event is `2/5` and the probability of non occurrence of another event is `3/10` if these events are independent then the probability that only one of the two events occurs is
View SolutionLet `alpha` be root of `x^(2)+x+1=0` and suppose that a fair die is thrown 3 times if a,b and c are the numbers shown on the die then the probability that `alpha^(a)+alpha^(b)+alpha^(c )` =0 is
View SolutionSuppose that a bag a contains n red and 2 black balls and another bag B contains 2 red and n black balls one of the two bags is selected at random and two balls are dran from it at a time when it is known that the two balls drawn are red if the probability that those two balls drawn are from bag A is `6/7` then n=
View SolutionA rondom variable X has its range {-1,0,1} if its mean is 0.2 and P(x=0) =0.2 then P(x=1) =
View SolutionThere are 800 families with four children in each family Assuming equal channce for every child to be a boy or a girl the number of familes expected to have children of both sexes is
View SolutionA straight line meets the X and y axes at the points A,B respectively if AB=6 units then the locus of the point P which divides the line segment AB such that AP:PB =2 :1 is
View SolutionIf the area of the region bounded by the curves y=x =`x^(2)` and x = `y^(2)` is k then the area of the region bounded by the curves
`(x+sqrt(3y))/(2)=(sqrt(3x)-y^(2))/(2)` and `(sqrt(3x)-y)/(2)=(x+sqrt(3y))^(2)/(2)` is
View SolutionThe set of values that `beta` can assume so that the pont `(0,beta)` should lie on or inside the triangle having sides 3x+y+2=0 ,2x-3y+5=0 and x+4y-14=0 is
View SolutionIf `(lambda^(2),lambda+1) lambda in z` belong to the region between the lines x+2y-5 =0 and 3x-y+1=0 which includes the origin then the possible number of such point is
View SolutionIf the mid points of the sides BC, CA and AB of a triangle ABC are respectively (2,1) (-01,-2)and (3,3) then the equation of the side BC is
View SolutionThe distance between the pair of lines represented by
`x^(2)+2sqrt(2)xy+2y^(2)+4x+4sqrt(2)y+1=0`, is
View SolutionA pair of lines S =0 together with the lines given by the equation
`8x^(2)-14xy+3y^(2)+10x+10y-25=0` form a parallelogram if its diagonals intersect at point (3,2) then the equation S=0 is
View SolutionIf the equation of the circle having its centre in the second quadrant touches the
corrdinate axes and also the line `(x)/(5)+(y)/(12)=1` is `x^(2)+y^(2)+2lambdax-2lambday+lambda^(2)=0` then `lambda=`
View SolutionThe equation of circel passing throught the point (2,8) touching the lines
4x-3y-24=0 and 4x+3y-42=0 and having the x coordinate of its centre less than or equal to 8 is
View SolutionThe point of intersecntion of the common tangents drawn to the circles
`x^(2)+y^(2)-4x-2y+1=0` and `x^(2)+y^(2)-6x-4y+4=0` is
View SolutionThe circle S=0 cuts the circle `x^(2)+y^(2) -4x+2y-7=0` orthogonally if (2,3) is the centre of the circle S=0 then its radius is
View SolutionThe equation of the circle which cuts the circles
`S_(1)=x^(2)+y^(2)-4=0`
`S_(2)=x^(2)+y^(2)-6x-8y+10=0`
`S_(3)=x^(2)+y^(2)+2x-4y-2=0`
at the extremites of diameters of these circles is
View SolutionThe length of the latusrectum of the parabola `20(x^(2)+y^(2)-6x-2y+10)=(4x-2y-5)^(2)` is
View Solutiony=3x-2 is a straight line touching the parabola `(-3)^(2)=12(x-2)` if a line drawn perpendicular to this line at p on it touches the given parabola then the point p is
View SolutionIf (l,m) is the circumcentre of an equailateral triangle inscribed in the ellipse `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1`
having verticles at points with ecentric angles `theta_(1),theta_(2)` and `theta_(3)` then
`2/3[cos(theta_(1)-theta_(2))+cos(theta_(2)-theta_(3)+cos(theta_(3)-theta_(1))]` =
View SolutionThe sides of the rectangle of greatest area that can be inscribed in the ellipse `x^(2)+4y^(2)=64` are
View SolutionIf ` 2x-ky +3=0 ,3x -y+1 =0 ` are conjugate lines with respect to ` 5x^(2) -6y^(2) = 15 ` then k=
View SolutionThe points A(2,-1,4),B(1,0,-1),C(1,2,3) and D(2,1,8) form a
View Solution
Mathematics questions and complete solutions for chapter AP EAMCET ENGINEERING ENTRANCE EXAM of TS EAMCET PREVIOUS YEAR PAPERS of Class 12