Complete Solutions to MATHEMATICS of chapter AP EAMCET ENGINEERING ENTRANCE EXAM ONLINE QUESTION PAPER 2019 (SOLVED) of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | AP EAMCET ENGINEERING ENTRANCE EXAM ONLINE QUESTION PAPER 2019 (SOLVED) |
| TS EAMCET | MATHEMATICS |
| Number Of Questions | 80 |
| Academic Year | 2023-24 |
`f(x)=x/(e^x-1)+x/2+2cos^3 x/2` on R-{0} is
03:34View SolutionConsider the following units
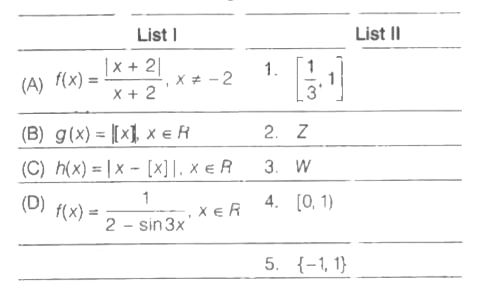 View Solution
View SolutionAssertion (A)
`(1)+(1+2+4)+(4+6+9)+(9+12+16)+……+(81+90+100)=1000`
Reason ( R) `sum_(r=1)^11(r^3-[r-1]^3)=n^3` for any natural number n05:57View SolutionIF `{:[(1,0),(0,-1):}]` , `P={:[(1,1),(0,1):}] and X=APA^T` then `A^TX^(50) A=`
05:20View SolutionIF [x] is the greatest integer less than or equal to x and IxI is the modulus of x, then the system of three equations
2x+3|y|+5[z]=0,x+|y|-2 [z]=4, z+|y|+[z]=1` hasView SolutionInvestigate the values of `lamda and mu` for the system `x+2y+3z=6,x+3y+5z=9,2x+5y+lamdaz=mu` and match the values in List-I with the terms in List -II
 10:47View Solution
10:47View SolutionIF `z=x +iy,x,y, in R, (x,y) ne (0,-4)` and Arg `((2z-3)/(z+4i))=pi/4`, then the locus of z is
06:51View SolutionIF `z=x+iy,x,y in R` and the imaginary part of `((overlinez-1)/(overlinez-i))` is 1,then the locus of z is
06:44View SolutionIF `omega` represents a complex cube root of unity, then `(1+1/omega)(1+1/omega^2)+(2+1/omega)(2+1/omega^2)+...+(n+1/omega)(n+1/omega^2)=`
05:33View SolutionIF `omega` is a complex cube root of unity
`sum_(r=1)^9r(r+1-omega)(r+1-omega^2)=`05:09View SolutionIF `alpha and beta` are the roots of `x^2+7x+3=0` and `(2alpha)/(3-4alpha),(2beta)/(3-4beta)` are the roots of `ax^2+bx+c=0` and GCD of a,b,c is 1, then a+b+c=
06:12View SolutionIF `alpha , beta` are the roots of `x^2+bx+c=0, gamma,delta` are the roots of `x^2+b_1x+c_1=0 and gamma lt alpha lt delta lt beta`, then `(c-c_1)^2 lt`
View SolutionLet a,b and s be the sides of a scalane triangle. IF `lamda` is a real number such that the roots of the equation
`x^2+2(a+b+c)x+3 lamda (ab+bc+ca)=0` are real, then the interval in which `lamda` lies isView SolutionThe polynomial equation of degree 4 having real coefficients with three of its roots as `2 pm sqrt3 and 1+2i` is
03:54View SolutionAll the letters of the work ANIMAL are permuted in all possible ways and the permutations thus formed are arranged in dictionary order. IF the rank of the work ANIMAL is x, then the permutation with rank x, among the permutations obtained by permuting the letters of the word PERSON and arranging the permutations thus formed in dictionary order is
View SolutionA student is allowed to choose atmost n books from a collection of 2n+1 books. IF the total number of ways in which he can select atleast one book is 255, then the value of n is
05:45View SolutionThe sum of all the coefficients in the binomial expansion of `(1+2x)^n` is 6561. Let `R=(1+2x)^n=1+F`, where `1 in N` and `0 lt F lt 1`. IF `x=1/sqrt2` then `1-F/(1+(sqrt2-1)^4)`=
View SolutionIf `(1-px)^-1/((1-qx))=a_0+a_1x+a_2x^2+a_3x^3+.......` then `a_n=`
06:16View SolutionIF `3/((x-1)(x^2+x+1))=1/(x-1)-(x+2)/(x^2+x+1)=f_1(x)-f_2(x)and-(x+1)/((x-1)^2(x^2+x+1))=Af_1(x)+(B+D/(x-1)) f_2(x)=C/(x-1)^2,A+B+C+D=`
View SolutionLet M and m respectively denote the maximum and the minimum values of `[f(theta)^2],where f(theta)=sqrt(a^2+cos^2theta+b^2sin^2theta)+sqrt(a^2 sin^2 theta+b^2 cos^2 theta).` Then M-m=
View SolutionIF` cos A=(-60)/61 and tan B=-7/24` and neither A nor B in the second quadrant, then the angle `A+B/2` lies in the quadrant
View Solution`cos^2 5^@-cos^2 15^@-sin^2 15^@+sin^2 35^@+ cos15^@ sin15^@- cos5^@ sin35^@=`
View SolutionIF `cos theta ne 0, and sec theta-1=(sqrt2-1) tan theta` then `theta=`
03:52View Solution`cot[sum_(n=3)^32cot^-1(1+sum_(k=1)^n2K)]`=
View SolutionIF `sin x cos h y= cos theta, cos x sin h y= sin theta and 4 tan x=3`.Then, `sinh^2y=`
04:28View SolutionIn triangle ABC, if
`(b+c)/9=(c+a)/10=(a+b)/11,then (cosA+cosB)/cosC=`06:51View SolutionIn a `Delta ABC`, with usual notation, match the items in List-I with the terms in List-II and choose the correct option.
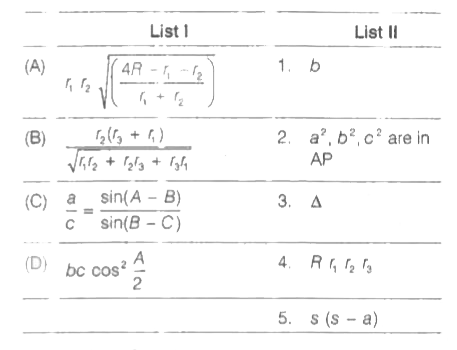 View Solution
View SolutionIf a,b and c are the sides of `Delta ABC` for which `r_1=8,r_2=12 and r_3=24` then the ordered triad (a,b,c)=
03:21View SolutionIf 4i + 7j + 8k, 2i + 3j + 4k, 2i + 5j + 7k are position vectors of A, B, C of `Delta` ABC then position vector of the point where the bisector of angle A meets BC is
05:10View SolutionThe equation of the plane passing through the point `hati+2hatj-hatk` are perpendicular to the line of intersection of the planes
`r.(3hati-hatj+hatk)=1andr.(hati+4hatj-2hatk)=2`, isView SolutionIf the position vectors of the vertices A,B and C of `Delta ABC` are `hati+2hatj-5hatk,-2hati+2hatj+hatk and 2hati+hatj-hatk` respectively, then `angle B=`
05:13View SolutionIF the position vectors of the vertices of a `Delta ABC` are `OA=3hati+hatj+2hatk,OB=hati+2hatj+3hatkand OC=2hati+3hatj+hatk` , then the length of the altitude of `Delta ABC` drawn from A is
05:17View SolutionA new tetrahedron is formed by joining the centroids of the faces of a given tetrahedron OABC. Then the ratio of the volume of the new tetrahedron to that of the given tetrahedron is
View SolutionLet `A=2hati+hatj-2hatk and B= hati+hatj`. If C is a vector such that `A.C=|C|,|C-A|=2 sqrt2` and the angle between `A times B` and C is `30^@`, then the value of `|(A times B) times C|` is
04:44View SolutionIF `a_0,a_1….,a_11` are the arithmetic progression with common difference d, then their mean deviation from their arithmetic mean is
View SolutionThe variance of the following continuous frequency distribution is
 04:53View Solution
04:53View SolutionIF two sections of strengths 30 and 45 are formed from 75 students who are admitted in a school,then the probability that two particular students are always together in the same section is
09:05View SolutionA bag contains 2n coins out of which n-1 are unfair with heads on both sides and the remaining are fair. One coin is picked from the bag at random and tossed. If the probability that head falls in the toss is `41/56`, then the number of unfair coins in the bag is
05:30View SolutionBag A contains 6 Green and 8 Red balls and bag B contain 9 Green and 5 Red balls . A card is drawn at random from a well shuffled pack of 52 playing cards. IF is a spade, two balls are drawn at random from bag A, otherwise two balls are drawn at random from bag B. IF the two balls are found to be of the same colour, then the probability that they are drawn from bag A is
View SolutionA random variable X has the probability distribution
 View Solution
View SolutionIn a poisson distribution with unit mean, `sum_(x=0)^infty|x-overlinex|P(X=x)=(overlinex` is the mean of the distribution).
View SolutionTwo straight rods of lengths 2a and 2b move along the coordinate axes in such a way that their extremities are always concyclic. Then the locus of the centres of such circles is
03:48View SolutionWhen the coordinate axes ar rotated about the origin in the positive direction through an angle `pi/4`, IF the equation `25x^2+9y^2=225` is transformed to `ax^2+betaxy+ygamma^2=delta`, then `(alpha+beta+gamma-sqrtdelta)^2`=
View SolutionThe equation of the line through the point of intersection of the lines 3x-4y+1=0 and 5x+y-1=0 and making equal non-zero intercepts on the coordinate axes is
05:05View SolutionThe line through P(a,2) where `a ne 0`, making an angle `45^@` with the positive direction of the X-axis meet the curve `x^2/9+y^2/4=1` at A and D and the coordinate axes at B and C. IF PA, PB, PC and PD are in the geometric progression, then 2a=
View SolutionIf the equations of the perpendicular bisectors of the sides AB and AC of a `Delta` ABC are x - y + 5 = 0 and x + 2y =0 respectively and if A is (1,-2), then the equation of the perpendicular bisector of the side BC is
06:01View SolutionIf each line of a pair of lines passing through origin is at a perpendicular distance of 4 units from the point (3,4) then the equation of the pair of lines is
05:00View SolutionVariable straight lines y=mx+c make intercepts on the curve `y^2 -4ax=0` which subtend a right angle at the origin. Then the point of concurrence of these lines y=mx+c is
View SolutionThe abscissae of two points P,Q are the roots of the equation `2x^2+4x-7=0` and their ordinates are the roots of the equation `3x^2-12x-1=0`. Then the centre of the circle with PQ as a diameter is
03:07View SolutionThe angle between a pair of tangents drawn from a point P to the circle `x^(2)+y^(2)+4x-6y+9sin^(2)alpha+13 cos^(2)alpha=0" is "2alpha`. The equation of the locus of the point P is
07:20View SolutionThe equation to the circle whose radius is 3 and which touches internally the circle `x^(2)+y^(2)-4x+6y-12=0" at this point (-1,1) is"`
06:45View SolutionSuppose that the circle `x^2+y^2+2gx+2fy+c=0` has its centre on `2x+3y-7=0` and cuts the circles `x^2+y^2-4x-6y+11=0` and `x^2+y^2-10x-4y+21=0` orthogonally. Then `5g-10f+3c=`
View SolutionIf the radical axis of the circles `x^2+y^2+2gx+2fy+c=0` and `2x^2+2y^2+3x+8y+2c=0` touches the circle `x^2+y^2+2x+2y+1=0`, then `(4g-3)(f-2)=`
07:18View SolutionThe parabola `x^2=4ay` makes an intercept of length `sqrt40` units on the line `y=1+2x` then a values of 4a is
05:37View SolutionThe locus of the points of intersection of perpendicular normals of the parabola `y^2=4ax` is
06:02View SolutionP is a variable point on the ellipse `x^2/a^2+y^2/b^2=1` with foci `F_1 and F_2`. IF A is the area of the triangle `PF_1,F_2`, then the maximum value of A is
View SolutionIf the line joining the point A (a) and `B(beta)` on the ellipse `x^2/25+y^2/9=1` is a focal chord, then one possible value of `cot""alpha/2.cot""beta/2` is
View SolutionThe equation of a tangent to the hyperbola `16x^2-25y^2-96x+100y-356=0` which makes an angle `45^@` with its transverse axis is
07:09View SolutionIf P(0,7,10), Q(-1,6,6) and R (-4,9,6) are three points in the space , then PQR is
07:02View SolutionA(2,3,5), B(a,3,3) and `C(7,5,beta)` are the vertices of a triangle. If the median through A is equally inclined with the co-ordinate axes, then `cos^-1(alpha/beta)=`
View SolutionThe plane `3x+4y+6z+7=0` is rotated about the line `r=(hati+2hatj-3hatk)+t(2hati-3hatj+hatk)` until the plane passes through origin. The equation of the plane is the new position is
View SolutionIF `lim_(x toinfty){(x^3+1)/(x^2+1)-(alphax+beta)}` exist and equal to 2, then the ordered pair `(alpha,beta)` of real numbers is
View SolutionFor `k gt0,sum_(x=0)^inftyk^x/(x!)lim_(n toinfty)(n!)/((n-x)!)(1-k/n)^(n-x)(1/n)^x=`
View SolutionLet `f:R to R` be the function defined by
`f(x)={{:(5,if,xlt1),(a+bx,if,1ltxlt3),(b+5x,if,3lexlt5),(30,if,x ge 5):}` then f isView SolutionLet [x] denote the greatest integer less than or equal to x, Then the number of points where the function `y=[x]+1|1-x|,-1 le x le 3` is not differentiable, is
View SolutionIf `sqrt(1-x^6)+sqrt(1-y^6)=a(x^3-y^3), then y^2(dy)/(dx)=`
View SolutionIf y=f(x) is twice differentiable function such that at a point `P,(dy)/(dx)=4,(d^2y)/(dx^2)=-3, then ((d^2x)/(dy^2))=`
03:23View SolutionThe time T of oscillation of a simple pendulum of length L is governed by `T=2pisqrt(L/g)`, where g is a constant. The percentage by which the length be changed in order to correct an error of loss equal to 2 minutes of time per day is
View SolutionLet A,G,H and S respectively denote the arithmetic mean, geometric mean, harmonic mean and the sum of the numbers `a_1,a_2,a_3……..a_n`. Then the value of x at which the function `f(x)=sum_(k=1)^n(x-a_k)^2` has minimum is
03:54View SolutionFor `m gt1, n gt 1` the value of c for which the Rolle's theorem is applicable for the function `f(x)=x^(2m-1)(a-x)^(2n)` in (0,a) is
06:39View SolutionIf the function `f:[-1,1]to R` defined by
View Solution`int ((x-1)dx)/((x+1)sqrt(x^(3)+x^(2)+x))=`
04:25View SolutionIf `I(x)=intx^2(logx)^2dx and I(I)=0` then I(x)
View Solution`int(x^5dx)/((x^2+x+1)(x^6+1)(x^4-x^3+x-1))=`
View Solution`int(dx)/(x+sqrt(x-1))`=
View Solution`int_(log2)^(t)(dx)/(sqrt(e^(x)-1))=(pi)/(6)`, then t=
04:09View Solution`int_0^1(log_e(1+x))/(1+x^2)dx=`
View SolutionIF the area of the circle `x^2+y^2=2` is divided into two parts by the parabola `y=x^2`, then the area (in sq units) of the larger part is
View SolutionIf c is a parameter, then the differential equation of the family of curves `x^2=c(y+c)^2` is
03:30View SolutionIF f(x), f'(x) f''(x) are positive functions and f(0)=1, f')0)=2 then the solution of the differential equation `{:|(f(x)f'(x)),(f'(x) f''(x))|=0` is
View Solution
MATHEMATICS questions and complete solutions for chapter AP EAMCET ENGINEERING ENTRANCE EXAM ONLINE QUESTION PAPER 2019 (SOLVED) of TS EAMCET PREVIOUS YEAR PAPERS of Class 12
