Complete Solutions to Mathematics of chapter AP EAMCET SOLVED PAPER 2018 ( 23-04-2019,SHIFT -1) of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | AP EAMCET SOLVED PAPER 2018 ( 23-04-2019,SHIFT -1) |
| TS EAMCET | Mathematics |
| Number Of Questions | 39 |
| Academic Year | 2023-24 |
When the coordinate axes are rotated by an angle `tan^(-1) ((3)/(4))` about the origin, then the equation `x^(2) + y^(2) =9` is transformed to the equation.
View SolutionIf the lines `x+ay=a=0, bx+y+b=0, cx+cy+1=0` (a,b,c being distinct and `!=1`) are concurrent, then the value of `(a/(a-1)+b/(b-1)+c/(c-1))` is
View SolutionIf `ad-bc ne 0`, then the area (in sq. units) of the parallelogram formed by the lines `ax + by + 2=0, ax + by + 5 = 0, cx + dy + 3 = 0 and cx + dy + 7 = 0` is
View SolutionThe circumcentre of the triangle with vertices at `(-2,3), (1,-2) and (2,1)` is
View SolutionIf the straight line `2x + 3y + 1 = 0` bisects the angle between a pair of lines, one of which in this pair is `3x + 2y + 4 = 0`, then the equation of the other line in that pair of lines is
View SolutionThe area of the triangle formed by the straight line x + y = 3 and the angle bisectors of the pair of straight lines `x^(2)-y^(2)+2y=1` is
View SolutionThe product of the lengths of the perpendiculars drawn from the point `(-1,5)` to the pair of lines `2x^(2) - xy - 3y^(2) + 6x + y + 4 = 0` is
View SolutionABCD is a square with side 16 units and A is the origin. If the equation of the circle circumscribing the square ABCD is `x^(2) + y^(2) = 4k(x + y)`, then k=
View SolutionIf a point P is moving such that the lengths of tangents drawn from P to the circles
`x^(2)+y^(2)-4x-6y-12=0` and
`x^(2)+y^(2)+6x+18y+26=0` are the ratio 2:3, then find the equation to the locus of P.
View SolutionIf the lines `2x + y + 12 = 0, kx -3y - 10 = 0` are conjugate with respect to the circle `x^(2) + y^(2) - 4x + 3y -1 = 0`, then k =
View SolutionThe length of the transverse common tangent of the circle `x^(2) + y^(2) - 2x + 4y + 4 = 0 and x^(2) + y^(2) + 4x -2y + 1 = 0` is
View SolutionIf the angle between the circles
`x^2 + y^2 - 12x - 6y + 41 = 0` and
`x^2 + y^2 + kx + 6y - 59 = 0` is `45^@` find k.
View SolutionIf the lengths of the tangents drawn from a point P to the three circles `x^(2) + y^(2) - 4 = 0, x^(2) + y^(2) -2x + 3y = 0 and x^(2) + y^(2) + 7y -18 = 0` are equal, then the coordinates of P are
View SolutionFor the parabola `y^(2) + 6y- 2x + 5 =0`, match the items in List-I with the suitable item in List-II given below:
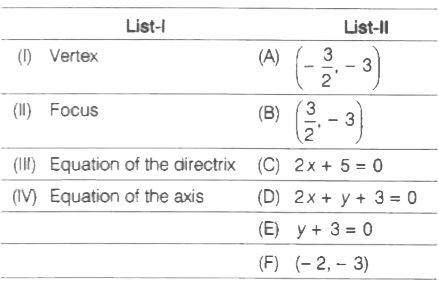
The correct matching is
View SolutionIf `5x -2y + k =0` is a tangent to the parabola `y^(2) = 6x`, then their point of contact is
View SolutionIf the minor axis of an ellipse subtends an angle `90^(@)` at each focus then the eccentricity of the ellipse is
View SolutionThe points of intersection of the perpendicular tangents drawn to the ellipse `4x^(2) + 9y^(2) = 36` lie on the curve.
View SolutionIf the eccentricity of a hyperbola is `(5)/(3)`, then the eccentricity of its conjugate hyperbola is
View SolutionIf the vertices of a `Delta ABC` are A = (2, 3, 5), `B = (-1, 3, 2), C = (3,5, -2)` then the area of the `DeltaABC` (in sq. units) is
View SolutionIf a line makes angles `tan^(-1) sqrt7, tan^(-1) (sqrt5)/(sqrt3)` with x-axis, Y-axis respectively, then the angle made by it with Z-axis is
View SolutionA plane passes through the point (3, 5, 7). If the direction ratios of its normal are equal to the intercepts made by the plane `x + 3y + 2z = 9` with the coordinate axes, then the equation of that plane is
View SolutionIf `f: [0,2) rarr` R is defined by `f(x) = {(1 + (2k)/(k) " for " ,0 le x lt 1),(kx " for ",1 le x lt 2):}` where `k gt 0`, and f is such that `underset(x rarr 1)(lim) f(x) = underset(x rarr 1)(lim) f(x)`, then the value of `k^(2)` is
View SolutionIf the function `f : R rarr R` defined by `f(x) = {((sin(a +1) x + sin x)/(x),x lt 0),((sqrt(x + x^(2)) - sqrtx)/(x^(1//2)),x gt 0):}` continuous on R, then `a + b`=
View SolutionLet f be defined on D = `R-{-1,1}` by `f(x) = (|x|)/(1-|x|)`, then
View SolutionIf `x= sec theta - cos theta, y = sec' theta - cos'' theta`, then `(dy)/(dx) =`
View SolutionIf `y = a sin x + (5 + 2x) cos x, " then " y'' + y =`
View SolutionThe area (in sq. units) of the triangle formed by the tangent and the normal at the point `((a)/(sqrt2), (b)/(sqrt2))` to the curve `(x^(2))/(a^(2)) + (y^(2))/(b^(2))=1` and the X-axis is
View SolutionThe interval in which the function `f(x) = 2x^(2) -` log x, for `x gt 0` decreases, is
View SolutionIf `f(x) = (x-1) (x-2) (x-3) " for ' x in [0,4]` then the value of `c in (0,4)` satisfying Lagrange's mean value theorem, is
View SolutionThe curve `f(x) = e^(x) sin x` is defined in the interval `[0, 2pi]`. The value of x for which the slope of the tangent drawn to the curve at x is maximum, is
View Solution`int ((x-1)dx)/((x+1)sqrt(x^(3)+x^(2)+x))=`
View Solution`int (cos^(3)x + cos^(5) x)/(sin^(2)x + sin^(4) x) dx =`
View Solution`int (dx)/(tan x + cot x + sec x + cosec x) =`
View SolutionIf `f(x) = int cosec^(2) x dx`, then `f ((pi)/(4)) =`
View SolutionIf a and b are positive integers such that `b gt a` then `underset(n rarr oo)(lim) [(1)/(na) + (1)/(na + 1) + (1)/(na + 2) + ….+ (1)/(nb)]=`
View Solution`int_(0)^(pi) (x tan x)/( sec x + tan x) dx=`
View SolutionThe area in the first quadrant enclosed by the axis, the line `x=ysqrt(3)` and the circle `x^(2)+y^(2)=4` is
View SolutionIf l and m are the degree and the order respectively of the differential equation of the family of all circles in the XY plane with radius 5 units. Then 2l + 3m =
View SolutionAn integrating factor of the differential equation `cos^(2) x (dy)/(dx) - (tan 2x) y = cos^(4) x` is
View Solution
Mathematics questions and complete solutions for chapter AP EAMCET SOLVED PAPER 2018 ( 23-04-2019,SHIFT -1) of TS EAMCET PREVIOUS YEAR PAPERS of Class 12