Complete Solutions to Mathematics of chapter TS EAMCET 2018 (4 MAY SHIFT 1) of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | TS EAMCET 2018 (4 MAY SHIFT 1) |
| TS EAMCET | Mathematics |
| Number Of Questions | 80 |
| Academic Year | 2023-24 |
Let `f:R to R,g:R to R` be differentiable functions such that (fog)(x) = x. If `f(x)=2x+cosx+sin^(2)x`, then the value of `underset(n=1)overset(99)sumg(1+(2n-1)pi)` is
View SolutionIf `f:[1,oo)to[1,oo]` is defined by
`f(x)=(1+sqrt(1+4log_(2)x))/(2)`, then `f^(-1)(3)=`
View SolutionIf `alpha` and `beta` are the greatest divisors of `n(n^(2)-1)` and `2n(n^(2)+2)` respectively for all `n in N`, then `alpha beta=`
View SolutionLet `A=[{:((1)/(6),(-1)/(3),(-1)/(6)),((-1)/(3),(2)/(3),(1)/(3)),((-1)/(6),(1)/(3),(1)/(6))]`. If
`A^(2016l)+A^(2017m)+A^(2018n)=(1)/(alpha)A`, for every `l,m,n in N`, then the value of `alpha` is
View SolutionLet `l, m, n in R` and `A=[{:(1, r, r^(2),l),(r, r^(2),1,m),(r^(2),1,r,n):}]`. Then, the set of all real values of r for which the rank of A is 3, is
View SolutionThe following system of equations `x+y+z=9`, `2x+5y+7z=52` and `x+7y+11z=77` has
View SolutionZ is a complex number such that `|z| le 2` and `-(pi)/(3)le"amp Z"le(pi)/(3)`. The area of the region formed by locus of Z is
View SolutionThe points in the argand plane given by
`Z_(1)=-3+5i,Z_(2)=-1+6i,Z_(3)=-2+8i,Z_(4)=-4+7i` form a
View SolutionWhen `n=8,(sqrt(3)+i)^(n)+(sqrt(3)-i)^(n)=`
View SolutionIf `2" cis "(7pi)/(5)` is one of the values of `z^(1//5)`, then z =
View SolutionThe set of real values of x for which the inequality `|x-1|+|x+1|lt 4` always holds good is
View SolutionIf the roots of the equation `x^(2)+x+a=0` exceed a, then
View SolutionIf the roots of the equation `sqrt((x)/(1-x))+sqrt((1-x)/(x))=(5)/(2)` are p and `q(q gt q)` and the roots of the equation `(p+q)x^(4)-pqx^(2)+(p)/(q)=0` are `alpha,beta,gamma,delta,` then `(sum alpha)^(2)-sum alpha beta+alpha beta gamma delta=`
View SolutionThe equation `x^(5)-5x^(3)+5x^(2)-1=0` has three equal roots. If `alpha,beta` are the other two roots of this equation, then `alpha+beta+alphabeta=`
View SolutionIf all possible numbers are formed by using the digits 1, 2, 3, 5, 7 without repetition and they are arranged in descending order, then the rank of the number 327 is
View SolutionIf a is the number of all even divisors and b is the number of all odd divisors of the number 10800, then `2a+3b=`
View SolutionIf the coefficient of `x^(5)` in the expansion of `(ax^(2)+(1)/(bx))^(13)` is equal to the coefficient of `x^(-5)` in the expansion of `(ax-(1)/(bx^(2)))^(13)`, then ab =
View SolutionFor `n in N`, in the expansion of `(root(4)(x^(-3))+a root(4)(x^(5)))^(n)`, the sum of all binomial coefficients lies between 200 and 400 and the term independent of x is 448. Then, the value of a is
View SolutionIf `(x^(4)+x^(3)+2x^(2)-2x+1)/(x^(3)+x^(2))`
`=P(x)+(A)/(x)+(B)/(x^(2))+( C )/(x+1)`, then `A+B+C=`
View SolutionIf `A(n)=sin^(n)alpha+cos^(n)alpha`, then
`A(1)A(4)+A(2)+A(5)`=
View SolutionWhen `(sin9 theta)/(cos27 theta)+(sin3 theta)/(cos9 theta)+(sin theta)/(cos 3 theta)=k`
`(tan 27 theta-tan theta)` is defined, then k =
View SolutionIf `0 lt theta lt pi/2, x = sum_(n=0)^(oo)cos^(2n) theta, y =sum_(n=0)^(oo)sin^(2n)theta`, and `z=sum_(n=0)^(oo) cos^(2n)theta sin^(2n) theta` then show that
(i) `xyz=xy+z` (ii) `xyz=x+y+z`
View SolutionNumber of solutions of the equation `sinx-sin2x+sin3x=2cos^(2)x-2cosx` is `(0,pi)` is
View Solution`2"Tan"^(-1)(1)/(5)+"Sec"^(-1)(5 sqrt(2))/(7)+"Tan"^(-1)(1)/(8)=`
View SolutionIf `cos h x=(sqrt(14))/(3),sin h x = cos theta` and `-pi lt theta lt -(pi)/(2)`, then `sin theta=`
View SolutionIn `DeltaABC`, if `a=5` and `tan((A-B)/(2))=(1)/(4)tan((A+B)/(2))`, then `sqrt(a^(2)-b^(2))`=
View SolutionIn a `DeltaABC`, if A = 2B and the sides opposite to the angles A, B, C are `alpha+1,alpha-1` and `alpha` respectively, then `alpha` =
View SolutionIn `DeltaABC`, right angled at A, the circumradius, inradius and radius of the cxcircle opposite to A are respectively in the ratio `2:5:lambda`, then the roots of the equation
`x^(2)-(lambda-5)x+(lambda-6)=0` are
View SolutionLet `3hati+hatj-hatk` be the position vector of a point B. Let A be a point on the line which is passing through B and parallel to the vector `2hati-hatj+2hatk`. If `|BA|=18`, then the position vector of A is
View SolutionThe vector that is parallel to the vector `2hati-2hatj-4hatk` and coplanar with the vectors `hati+hatj` and `hatj+hatk` is
View SolutionA line L is passing through the point A whose position vector is `hati+2hatj-3hatk` and parallel to the vector `2hati+hatj+2hatk`. A plane `pi` is passing through the points `hati+hatj+hatk, hati-hatj-hatk` and parallel to the vector `hati-2hatj`. Then, the point where this plane `pi` meets the line L is
View SolutionIf the position vectors of three points A, B, C respectively are `hati+2hatj+hatk,2hati-hatj+2hatk` and `hati+hatj+2hatk`, then the perpendicular distance of the point C from the line AB is
View SolutionThe volume of a tetrahedron whose vertices are `4hati+5hatj+hatk,-hatj+hatk,3hati+9hatj+4hatk` and `-2hati+4hatj+4hatk` is (in cubic units)
View SolutionIf the vectors b, c, d are not coplanar, then the vector `(axx b)xx(c xx d)+(a xx c)xx(d xx b)+(a xx d)xx(b xx c)` is
View Solution`x_(1),x_(2),….,x_(n)` are n observations with mean `vec(x)` and standard deviation `sigma`. Match the items of List - I with those of List - II

The correct answer is
View SolutionThe variance of 50 observations is 7. If each observation is multiplied by 6 and then 5 is subtracted from it, then the variance of the new data is
View SolutionTwo dice are thrown and two coins are tossed simultaneously. The probability of getting prime numbers on both the dice along with a head and a tail on the two coins is
View Solution5 persons entered a lift cabin on the ground floor of a 7 floor house. Suppose, that each of them independently and with equal probability can leave the cabin at any floor beginning with the first. The probability of all the 5 persons leaving the cabin at different floors, is
View SolutionA company produces 10000 items per day. On a particular day 2500 items were produced on machine A, 3500 on machine B and 4000 on machine C. The probability that an item produced by the machines A, B, C to be defective is respectively `2%,3%` and `5%`. If one item is selected at random from the output and is found to be defective, then the probability that it was produced machine C, is
View SolutionA randdom variable X takes the values 1, 2, 3 and 4 such that `2P(X=1)=3P`
`(X=2)=P(X=3)=5P(X=4)`. If `sigma^(2)` is the variance and `mu` is the mean of X. Then, `sigma^(2)+mu^(2)=`
View SolutionAn executive in a company makes on an average 5 telephone calls per hour at a cost of Rs. 2 per cell. The probability that in any hour the cost of the calls exceeds a sum of Rs. 4 is
View SolutionA quadrilateral ABCD is divided by the diagonal AC into two triangles of equal areas. If A, B, C are respectively, `(3,4),(-3,6),(-5,1),` then the locus of D is
View SolutionBy rotating the coordinate axes in the positive direction about the origin by an angle `alpha`, if the point (1, 2) is transformed to `((3sqrt(3)-1)/(2sqrt(2)),(sqrt(3)+3)/(2sqrt(2)))` in new coordinate system Then, `alpha` =
View SolutionLet `a ne0,bne0`, c be three real numbers and `L(p,q)=(ap+bq+c)/(sqrt(a^(2)+b^(2))), for all p,q in R`.
If `L((2)/(3),(1)/(3))+L((1)/(3),(2)/(3))+L(2,2)=0`, then the line `ax+by+c=0` always passes through the fixed point
View SolutionThe incentre of the triangle formed by the straight line having 3 as X-intercept and 4 as Y-intercept, together with the coordinate axes, is
View SolutionThe equation of the straight line in the normal form which is parallel to the lines `x+2y+3=0` and `x+2y+8=0` and dividing the distance between there two lines in the ratio 1 : 2 internally is
View SolutionA pair of straight lines is passing through the point (1, 1). One of the lines makes an angle `theta` with the positive direction of X-axis and the other makes the same angle with the positive direction of Y-axis. If the equation of the pair of straight lines is
`x^(2)-(a+2)xy+y^(2)+a(x+y-1)=0,a ne-2`, then the value of `theta` is
View SolutionIf the pair of lines `6x^(2)+xy-y^(2)=0` and `3x^(2)-axy-y^(2)=0,a gt 0` have a common line, then a =
View SolutionIf the chord `L -=y-mx-1=0` of the circle `S-=x^(2)+y^(2)-1=0` touches the circle
`S_(1)-=x^(2)+y^(2)-4x+1=0`, then the possible points for which L = 0 is a chord of contact of S = 0 are
View SolutionIf `y+c=0` is a tangent to the circle `x^(2)+y^(2)-6x-2y+1=0` at (a, 4), then
View SolutionIf the circles given by
`S-=x^(2)+y^(2)-14x+6y+33=0` and
`S'-=x^(2)+y^(2)-a^(2)=0(a in N)` have 4 common tangents, then the possible number of circles `S'=0` is
View SolutionThe centre of the circle passing through the point (1,0) and cutting the circles
`x^(2)+y^(2)-2x+4y+1=0` and
`x^(2)+y^(2)+6x-2y+1=0` orthogonally is
View SolutionThe equation of the tangent at the point (0, 3) on the circle which cuts the circles `x^(2)+y^(2)-2x+6y=0`,
`x^(2)+y^(2)-4x-2y+6=0` and
`x^(2)+y^(2)-12x+2y+3=0` orthogonally is
View SolutionIf two tangents to the parabola `y^(2)=8x` meet the tangent at its vertex in M and N such that MN = 4, then the locus of the point of intersection of those two tangents is
View SolutionThree normals are drawn from the point (c, 0) to the curve `y^(2)=x`. If one of the normals is X-axis, then the value of c for which the other two normals are perpendicualr to each other is
View SolutionIf the normal drawn at one end of the latus rectum of the ellipse `b^(2)x^(2)+a^(2)y^(2)=a^(2)b^(2)` with eccentricity 'e' passes through one end of the minor axis. Then,
View SolutionA variable tangent to the ellipse `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1` makes intercepts on both the axes. The locus of the middle point of the portion of the tangent between the coordinate axes is
View SolutionIf the eccentricity of a conic satisfies the equation `2x^(3)+10x-13=0`, then the conic is
View SolutionAssertion (A) If `(-1, 3, 2)` and `(5, 3, 2)` are respectively the orthocentre and circumcentre of a triangle, then (3, 3, 2) is its centroid.
Reason ( R ) Centroid of the triangle divides the line segment joining the orthocentre and the circumcentre in the ratio 1 : 2.
Which one of the following is true ?
View SolutionThe lines whose direction cosines are given by the relations `al+bm+cn=0` and `mn+nl+lm=0` are
View SolutionIf the plane passing through the points (1, 2, 3), (2, 3, 1) and (3, 1, 2) is `ax+by+cz=1`, then `a+2b+3c=`
View Solution`underset(x to -oo)lim(3|x|-x)/(|x|-2x)-underset(xto0)lim(log(1+x^(3)))/(sin^(3)x)=`
View SolutionIf `f(x)={{:((x-2)/(|x-2|)+a,x lt 2),(a+b,x=2),((x-2)/(|x-2|)+b,x gt 2):}`
is continuous at x = 2, then `a+b=`
View SolutionIf `f(x)={{:((x^(2)log(cosx))/(log(1+x^(2))),x ne 0),(0,x = 0):}`, then f is
View SolutionMatch the items given in List-I with those of the items of List - II
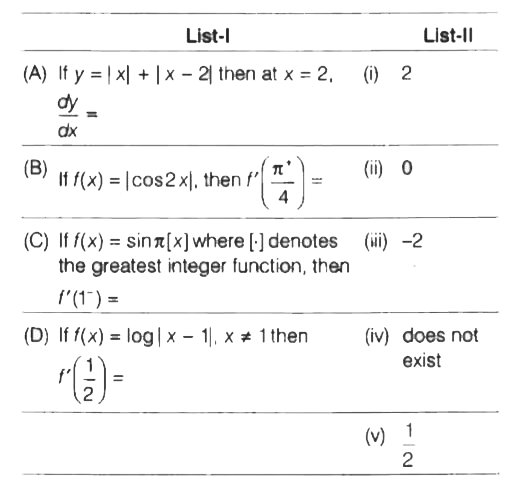
The correct answer is
View SolutionIf `y=((sin^(-1)x)^(2))/(2)`, then `(1-x^(2))y_(2)-xy_(1)=`
View SolutionIf the relative errors in the base radius and the height of a cone are same and equal to 0.02, then the percentage error in the volume of that cone is
View SolutionThe normal at a point `theta` to the curve `x=a(1+cos theta),y=a sin theta` always passes through the fixed point
View SolutionLet f(x) be continuous on [0, 6] and differentiable on (0, 6). Let f(0) = 12 and `f(6) = -4`.
If `g(x)=(f(x))/(x+1)`, then for some Lagrange's constant `c in (0,6),g'( c )=`
View SolutionIf `(alpha,beta)` and `(gamma,delta)` where `alpha lt gamma`, are the turning points of `f(x)=2x^(3)-15x^(2)+36x-8`, then `alpha-gamma-beta+delta=`
View SolutionThe height of a cylinder of the greatest volume that can be inscribed in a sphere of radius 3 is
View Solution`int(dx)/((e^(x)+e^(-x))^(2))=`
View Solution`int_(0)^(pi//2)(dx)/(1+(tanx)^(sqrt(2018)))=`
View SolutionIf `int(x)/((x^(2)+1)(x-1))dx=A log|x^(2)+1|+B tan^(-1)x+C log|x-1|+d`, then `A+B+C=`
View Solution`int_(0)^(pi//2)(cos^(3)x)/(sinx+cosx)dx=`
View Solution`int_(0)^(3)(2+x^(2))dx=`
View SolutionThe area enclosed (in square units) by the curve `y=x^(4)-x^(2)`, the X-axis and the vertical lines passing through the two minimum points of the curve is
View SolutionThe differential equation corresponding to the family of circles having centres on X-axis and passing through the origin is
View SolutionThe general solution of the differential equation `(x^(2)+xy)y'=y^(2)` is
View SolutionAt any point on a curve, the slope of the tangent is equal to the sum of abscissa and the product of ordinate and abscissa of that point. If the curve passes through (0, 1), then the equation of the curve is
View Solution
Mathematics questions and complete solutions for chapter TS EAMCET 2018 (4 MAY SHIFT 1) of TS EAMCET PREVIOUS YEAR PAPERS of Class 12